文章目录
- 向量
- 向量的模(向量的长度)
- 向量规范化
- 向量与向量
- 向量和向量之间的夹角(数字表示范围:[0,π],0度到180度 )
- 向量和x轴之间夹角(数字表示范围:[-π,π] ,-180度到+180度)
- 向量和x轴之间夹角(数字表示范围:[0,2π] ,0度到360度)
- 向量与面
- 向量与体
- 点与面
- 将点投影到面
- 点到面的距离
向量
向量的模(向量的长度)
l_norm = (lx**2+ly**2)**0.5
向量规范化
l_norm = (lx**2+ly**2)**0.5
lx = lx/l_norm
ly = ly/l_norm
向量与向量
向量和向量之间的夹角(数字表示范围:[0,π],0度到180度 )
import numpy as np
import scipy.linalg as laa = np.array([1,0])
b = np.array([0,0])
c = np.array([1,-1])ba = a - b
bc = c - bcosine_angle = np.dot(ba, bc) / (la.norm(ba) * la.norm(bc))
angle = np.arccos(cosine_angle)print (np.degrees(angle))
向量和x轴之间夹角(数字表示范围:[-π,π] ,-180度到+180度)
import numpy as np
import scipy.linalg as laa = np.array([1,0])
b = np.array([0,0])
c = np.array([1,-1])ba = a - b
bc = c - bcosine_angle = np.dot(ba, bc) / (la.norm(ba) * la.norm(bc))
angle = np.arctan2(bc[1], bc[0]) - np.arctan2(ba[1], ba[0])print (np.degrees(angle))
向量和x轴之间夹角(数字表示范围:[0,2π] ,0度到360度)
import numpy as np
import scipy.linalg as laa = np.array([1,0])
b = np.array([0,0])
c = np.array([1,-1])ba = a - b
bc = c - bcosine_angle = np.dot(ba, bc) / (la.norm(ba) * la.norm(bc))
angle = np.arctan2(bc[1], bc[0]) - np.arctan2(ba[1], ba[0])if angle<0:angle = np.pi*2 + angleprint (np.degrees(angle))
向量与面
待更新...
向量与体
待更新...
点与面
将点投影到面
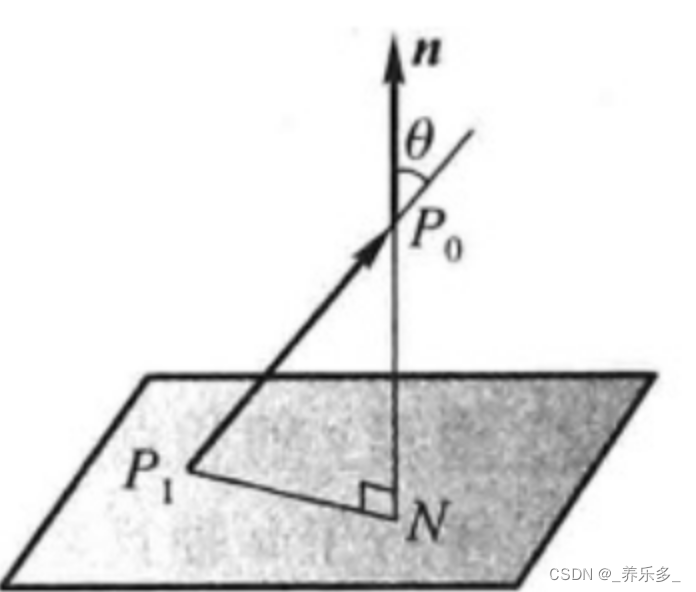
点到面的距离

空间上不共线的三个点P1,P2,P3确定一个平面,计算空间上某个点P4到{P1,P2,P3}组成的平面的距离,可如下计算
import numpy as npdef define_area(point1, point2, point3):"""法向量 :n={A,B,C}空间上某点:p={x0,y0,z0}点法式方程:A(x-x0)+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)https://wenku.baidu.com/view/12b44129af45b307e87197e1.html:param point1::param point2::param point3::param point4::return:(Ax, By, Cz, D)代表:Ax + By + Cz + D = 0"""point1 = np.asarray(point1)point2 = np.asarray(point2)point3 = np.asarray(point3)AB = np.asmatrix(point2 - point1)AC = np.asmatrix(point3 - point1)N = np.cross(AB, AC) # 向量叉乘,求法向量# Ax+By+CzAx = N[0, 0]By = N[0, 1]Cz = N[0, 2]D = -(Ax * point1[0] + By * point1[1] + Cz * point1[2])return Ax, By, Cz, Ddef point2area_distance(point1, point2, point3, point4):""":param point1:数据框的行切片,三维:param point2::param point3::param point4::return:点到面的距离"""Ax, By, Cz, D = define_area(point1, point2, point3)mod_d = Ax * point4[0] + By * point4[1] + Cz * point4[2] + Dmod_area = np.sqrt(np.sum(np.square([Ax, By, Cz])))d = abs(mod_d) / mod_areareturn dif __name__ == '__main__':# 初始化数据point1 = [2, 3, 1]point2 = [4, 1, 2]point3 = [6, 3, 7]point4 = [-5, -4, 8]# 计算点到面的距离d1 = point2area_distance(point1, point2, point3, point4) # s=8.647058823529413print("点到面的距离s: " + str(d1))
本文链接:https://my.lmcjl.com/post/9346.html
展开阅读全文

4 评论