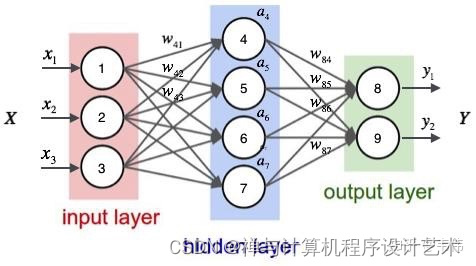
机器学习的问题中，过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据也希望模型可以进行正确的识别。 发生过拟合的原因，主要有以下两个： 模型拥有大量参数、表现力强。训练数据少。 那么如何来抑制过拟合 正则化是有效方法之一，它不仅可以有效降低高方差，还有利于降低偏差。何为 继续阅读

假若现在我们有如下的二维散点： x=1:10; y=[99.999 50.499 20.333 10.788 4.8111 2.7500 1.2322 0.4861 0.29501 0.1113498]; 在了解这些散点的大致分布之后，我们可以自己定义和其有相同单调性的函数来对散点进行拟合。 看其分布有点像对数函数，也有点像反函数，我们可以自定义函数： y = a*log(x 继续阅读

引言 众所周知的是，在大学课程中一般只会教授一种拟合方法(也即参数估计方法)——最小二乘法。这是一种直接求解的方法，非常的有效，不仅是损失最小解，而且是最大似然解。只不过，有一个缺点，它只能解决线性方程参数问题，对于非线性曲线，就无能为力了。大部分情况下还是将其转换成线性问题，再使用最小二乘法。 然而，并非所有的问题都能转换为线性问题，甚至 继续阅读

本文将从数据拟合的理论和应用角度出发，介绍二次函数数据拟合模型的相关知识和实际案例，并给出完整的代码示例，帮助读者更好地掌握二次函数拟合的方法和技巧。 一、基本概念 在数据分析和建模中，经常会遇到需要拟合一个函数曲线到已有数据点的情况。而二次函数是一种常见的、能够较好地拟合一些非线性数据的函数形式。 二次函数一般的形式为：$y=ax^2+bx+c$，其中 $a$、$b$、$c$ 分别是二次函数的系数，$x$ 为自变量，$y$ 为因变量。在二次函数中，$a$ 的 继续阅读

多分类问题 Softmax 高级优化算法 Adam Algorithm Intuition 每个参数有不同的学习率 卷积层 每个神经元只看前一层输入的一部分 原因： 1.更快的计算 2.需要更少的训练数据（不容易过度拟合） 模型评估 成本函数 分类 训练集用来训练参数w和b，而测试集用来选择多项式模型（即参数d），训练集不能评估w和b的好坏，类似的测 继续阅读

如果为了使各层拥有适当的广度，“强制性”地调整激活值的分布会怎样呢？实际上，Batch Normalization 方法就是基于这个想法而产生的 为什么Batch Norm这么惹人注目呢?因为Batch Norm有以下优点： 可以使学习快速进行(可以增大学习率)。不那么依赖初始值(对于初始值不用那么神经质) 。抑制过拟合(降低Dropout等的必要性)。 Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此&#xf 继续阅读

在神经网络的学习中，权重的初始值特别重要。实际上，设定什么样的权重初始值，经常关系到神经网络的学习能否成功。本节将介绍权重初始值的推荐值，并通过实验确认神经网络的学习是否会快速进行。 可以将权重初始值设为0吗 后面我们会介绍抑制过拟合、提高泛化能力的技巧 —— 权值衰减。 权值衰减就是一种以减小权重参数的值为目的进行学习的方法。 如果想减小权重的值，一开始就将初始值设为较小的值才是正途。实际上在这之前的权重初始值都是像0. 继续阅读

引言 随着人工智能技术的不断发展，越来越多的应用需要使用深度学习模型来解决。然而，传统的深度学习模型在处理一些复杂的问题时，往往会出现过拟合的情况，导致模型的性能下降。为了解决这个问题，循环神经网络模型应运而生。本文将介绍循环神经网络模型的基本原理、训练方法、应用场景以及优化策略。 一、循环神经网络模型的基本原理 神经网络模型是一种模拟人类神经系统的机器学习模型，可以用于解决各种问题，例如图像识别、自然语言处理、语音识别、推荐系统等等。神经网络模型由多个神经元组成，每个神经 继续阅读

加权最小二乘法（weighted least squares，简称WLS）是一种用于线性回归的方法，与普通最小二乘法相比，可以更好地处理误差方差不同的情况。接下来将从定义、优点、应用、示例等多个方面对加权最小二乘法python进行详细阐述。 一、定义 加权最小二乘法是一种用于处理误差方差不同的情况的线性回归方法。在加权最小二乘法中，误差较小的数据点给予更大的权重，误差较大的数据点给予更小的权重。这种方法可以更好地拟合真实数据，并且可以有效地提升模型的准确度。 继续阅读