目录 介绍 一、数组的创建和操作 通过 : 创建一维数组 通过logspace函数创建一维数组 通过linspace函数创建一维数组 二、数组的运算 数组的关系运算 数组的逻辑运算 三、矩阵 矩阵的构造 矩阵的下标引用 矩阵大小 四、矩阵元素的运算 矩阵的差分 矩阵运算 矩阵分析 矩阵分解 福利：文末有MATLAB全套资料哦 介绍 可以说，数组运算是 MATLAB 计算的基础，而数值数组是 MATLAB 最 继续阅读

Python中矩阵创建和矩阵运算 原文链接：https://blog.csdn.net/qian_fighting/article/details/79080711 矩阵创建和矩阵运算 矩阵创建 1、from numpyimport *; a1=array([1,2,3]) a2=mat(a1)  矩阵与方块列表的区别如下：   2、data2=mat(ones((2,4))) 创建一个2*4的1矩阵&#xff0 继续阅读

在计算机科学中，矩阵是一种非常重要的数据类型，它被广泛用于科学计算、图形学、机器学习等领域。在程序中，将一个数组转换为矩阵是必备的基本技能之一。 一、将一维数组转换为二维矩阵 在程序中，通常使用一维数组来表示矩阵。将一维数组转换为二维矩阵的方法如下： int[] arr = new int[]{1, 2, 3, 4, 5, 6}; int row = 2; int column = 3; int[][] matrix = new int[row][colum 继续阅读

Python是一种高级语言，用于Web开发，人工智能和机器学习等。它有着简单易学的语法以及丰富的开源库，使得开发者能够快速地完成任务。在本篇文章中，我们将探讨如何使用Python生成对角线为1的矩阵。 一、基础概念 在开始生成对角线为1的矩阵之前，我们需要了解一些基本概念。 矩阵是一个由固定数量的行和列组成的矩形数组。使用Python，我们可以使用列表（list）来表示矩阵。一个矩阵可以通过以下方式表示： matrix = [ [1, 0, 0], 继续阅读

我是小白，请多指教 我是小白，请多指教 我是小白，请多指教 intersect 函数 用去求取两个矩阵或者向量之间的交集。 具体形式 C = intersect(A, B)；C = intersect(A, B, ‘rows’)；[C, ia, ib] = intersect(A, B) 例子 C = intersect(A, B)； 两个矩阵或者向量之间&#xff0 继续阅读

对于矩阵操作，转置是很常见的一种操作。Python中也提供了简单的方法来实现矩阵转置操作。本文将从多个方面详细阐述Python中的矩阵转置代码。 一、概述 在Python中，我们可以使用zip函数来完成矩阵转置操作。zip函数可以将多个可迭代对象中对应的元素打包成一个元组，然后返回这些元组组成的对象。对于多个列表的打包，zip函数会以最短的列表长度来进行打包。因此，我们可以使用这种方式实现矩阵转置操作。 二、示例代码 matrix = [[1, 2, 3], 继续阅读

机器学习数学基础之Python矩阵运算 1.在Jupyter中写下Python矩阵基本运算学习记录1.1 python矩阵操作1.1.1 首先打开jupyter，引入numpy1.1.2 创建一个矩阵a并调用1.1.3 使用 shape可以获得矩阵大小1.1.4 使用下标读取矩阵中元素1.1.5 进行行列转换1.1.6 使用二维数组代替矩阵进行矩阵运算1.1.7 矩阵加减法1.1.8 加减失误案例1.1.9 成功案例 1.2 python矩阵乘法1.2.1 使用二维数组创建两 继续阅读

def matrixMultiply(A, B):# 获取A的行数和列数A_row, A_col = shape(A)# 获取B的行数和列数B_row, B_col = shape(B)# 不能运算情况的判断if(A_col != B_row):raise ValueError# 最终的矩阵result = []# zip 解包后是转置后的元组，强转成list, 存入result中BT = [list(row) for row in zip( 继续阅读

在Python编程中，我们常常需要对矩阵进行操作。而获取矩阵的某一列是一个常见需求，本文将介绍如何使用Python获取矩阵的某一列，并从以下几个方面进行详细阐述： 一、numpy库的方法 numpy是Python中一个常用的数学库，其中包含了许多操作矩阵的方法。我们可以使用其中的slice方法来获取矩阵的某一列。 import numpy as np # 创建一个5行3列的矩阵 matrix = np.array([[1, 2, 3], 继续阅读

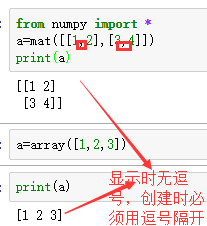
用numpy的库，没有去下。 创建矩阵 from numpy import *; a1=array([1,2,3]); a1=mat(a1);data1=mat(zeros((3,3))); #创建一个3*3的零矩阵，矩阵这里zeros函数的参数是一个tuple类型(3,3) data2=mat(ones((2,4))); #创建一个2*4的1矩阵，默认是浮点型的数据，如果需要时int类型&#xff0c 继续阅读

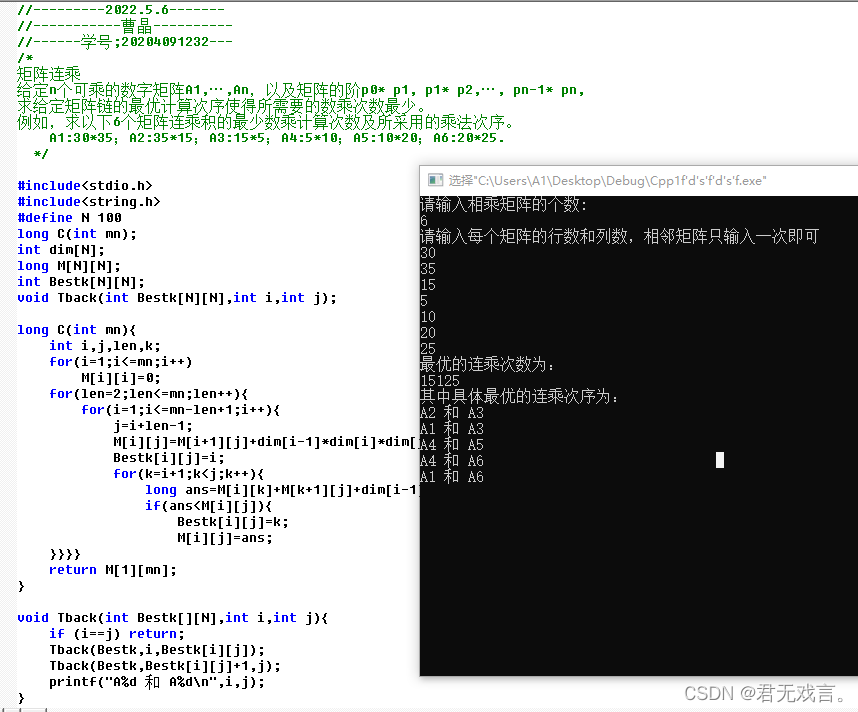
一、实验目的： 理解动态规划算法的基本思想和设计步骤； 掌握动态规划算法的典型应用范例——矩阵连乘。 二、实验内容 矩阵连乘 给定n个可乘的数字矩阵A1,…,An，以及矩阵的阶p0* p1, p1* p2,…, pn-1* pn,求给定矩阵链的最优计算次序使得所需要的数乘次数最少。 例如，求以下6个矩阵连乘积的最少数乘计算次数及所采用的乘法次序。     A1:30*35；A2:35*15；A3:15*5&# 继续阅读

使用Numpy模块中的内置方法实现矩阵相乘、逆序、转置和求和处理。 import numpy as npif __name__ == "__main__":# 矩阵相乘mat1 = np.mat([ [1, 3] ]) # 一行两列mat2 = np.mat([ [2], [4] ]) # 两行一列mat3 = mat1 * mat2print(mat3)# 矩阵求逆mat4 = np.mat([ [1, 0, 1], [0, 2 继续阅读