©Paperweekly 原创 · 作者 | An.

单位 | 中科院自动化所

研究方向 | 计算机视觉、模型压缩

论文标题：

SparseGPT: Massive Language Models Can Be Accurately Pruned in One-Shot

论文链接：

https://arxiv.org/pdf/2301.00774.pdf

本文提出了首个可以在千亿参数模型上高效准确工作的一次性剪枝算法——SparseGPT。该方法将剪枝问题简化为极大规模的稀疏回归问题，并设计了一个新的近似稀疏回归求解器，也解决分层剪枝问题。

SparseGPT 可以在最大的开源 GPT 模型（1750 亿参数）上仅用单个 GPU 耗时几小时就完成剪枝。同时，在无需任何微调的情况下，修剪上千亿（50~60%）参数后模型的精度几乎不变（甚至提升）。SparseGPT 还可以轻松地推广到半结构化剪枝（2:4 和 4:8），并且与权重量化方法结合。

千亿参数的剪枝挑战

以 chatGPT 为代表的大型语言模型（LLMs）取得了让世人瞩目的成果，但其庞大的规模和计算成本导致了极高的“入场费”。OpenAI 的 chatGPT 模型包含 1750 亿个参数，单是推理就需要至少 5 个 80GB 显存的 A100 GPU （保守估计至少 43 万元），更不用说研究所需要的训练。因此对大规模预训练模型的压缩十分重要且必要。

模型剪枝已在较小规模的模型（例如 BERT、ViT）中取得了很好的压缩效果。然而，表现最好的剪枝方法都需要对模型进行大量的再训练，以恢复删除元素造成的性能下降。正如上文所提到的，这一做法在 GPT 规模的模型上的代价极其昂贵。

最近出现了一些训练后剪枝方法 [1,2]，它们可以在不重新训练的情况下压缩模型。它们通常是将整个模型的压缩问题划分为分层子问题来求解，通过缩小每个压缩层和未压缩层之间输出的 误差，以保持压缩后整个模型的精度。该问题可表示为稀疏掩码 约束下剩余权重 的重建问题：

式（1）涉及对 和 的联合优化，该问题是 NP-hard 问题 [3]，常见做法是将问题再次分解为掩码选择（确定 ）和权重重建（确定 ）。单论权重重建问题，当掩码固定后，式（1）就变成了线性平方误差的凸优化问题，因此很容易优化。用标准线性回归公式可直接得到每个矩阵行 的封闭形式解：

式（1,2）的求解思路在少于 1 亿参数的 CNN 和 Transformer 模型上在几个小时内取得很好的压缩性能，但式（2）存在着一个“隐患”，的时间复杂度是 ，而每个矩阵行 都对应着不同的 ，即整体的时间复杂度高达 。这对于千亿规模的模型来说过于沉重了，例如 OBC [2] 这样的算法乐观估计也将耗时几周的时间，这其中还可能包括其他意想不到的巨大挑战。

快速近似重建

2.1 不同行海森矩阵的不一致问题

从第 1 节的分析可知，4 次方的计算复杂度主要源于每行的海森矩阵都不一致。正如图 1 所示，行掩码 通常是不同的，而 ，因此求解每一行时都需要单独求解掩码海森矩阵的逆。如果所有的行可以共享同一个海森矩阵，大量的求逆操作就可以省略，因此，设计一个既准确又高效的近似算法的关键是在具有不同修剪掩码的行之间重用海森矩阵。

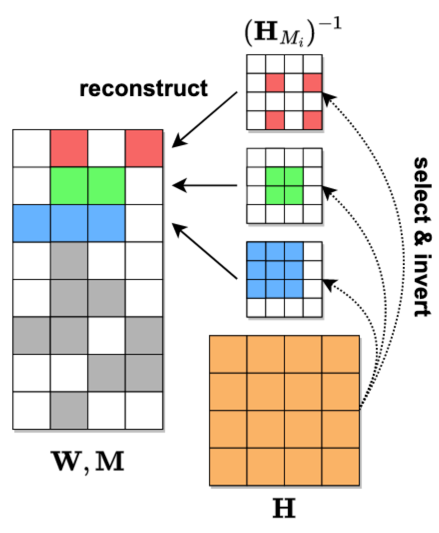
▲ 图1. 不同行海森矩阵的不一致问题（红、绿、蓝对应三行的掩码，掩码的不同导致掩码海森矩阵的不同）

2.2  基础：最优脑手术算法 OBS

为了解决上述问题，我先介绍下经典的 OBS [4]算法，它是训练后剪枝的鼻祖，可以实现逐个去除权重，并对其他权重进行补偿。OBS 的思想是找到在权重补偿后对损失函数影响最小的权重，即找到损失最小的权重索引 和对应的最优权重补偿量 （对所有权重进行补偿）。权重补偿导致的损失函数的变化的泰勒展开式如下：

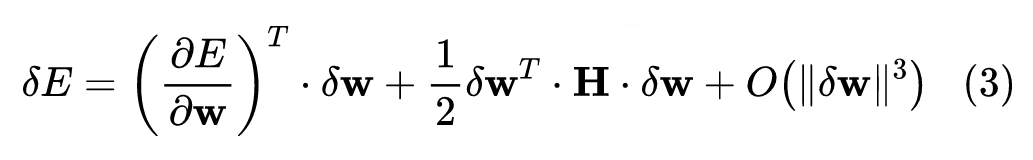
当达到局部极小值时，一次项和三次及高次项均可忽略。假设去掉索引 对应的权重，权重补偿量满足 的约束关系，即补偿量在 方向的分量正好和 抵消。由此可借助拉格朗日乘子法得到下式：

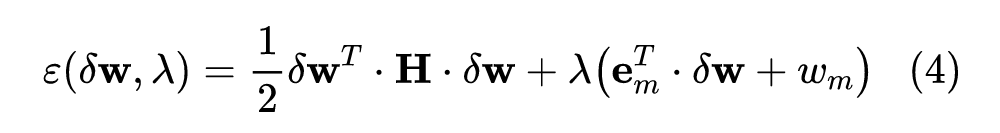
表示在去除 的条件下， 变化所导致的损失函数变化量，对 关于 求偏导，并消去 可得去除 对于的最优权重补偿量和最小损失函数变化量：

2.3 等价迭代视角

为了在具有不同修剪掩码的行之间重用海森矩阵，我们可以先从 OBS 的迭代视角来看逐行权重重建。由于逐层剪枝下 的每行的损失函数是二次函数，因此 OBS 对应的式（5）是准确的，即 是 的最优权重重构。

进一步讲，我们无须逐行直接求解完整的 ，而可以迭代应用 OBS 逐个修剪权重 直到 ，一次一个，最终将得到与直接应用完整 的标准封闭形式线性回归重建相同的最优解，即可以避免使用式（2）导致的多次求逆问题。

最优部分更新（OPU）：OBS 会对当前掩码 中所有可用参数的值进行更新，以尽可能补偿 去除的影响。为了进一步降低计算成本，作者对 OBS 进行了改进，只更新子集 中的所有剩余未修剪权重，这种部分更新只需使用 而非  计算 的权重补偿量。重要的是，对于 ，特定分层问题的损失仍是二次的，因此这种部分更新仍是最优的。随着迭代的进行， 的维度越来越小，整体的计算成本也将大大减少。

海森同步：在了解 OBS 和 OPU 原理后，我们可以利用它们的机制来实现在 的所有行上同步掩码海森的目标。为了简单起见，我们假设输入特征的顺序是固定的 ，我们递归地定义 索引的子集 的序列为：

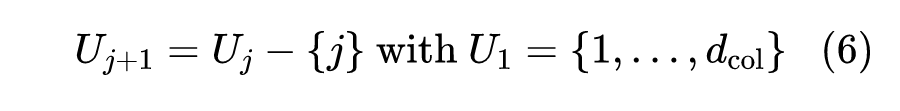
从 所有索引的集合开始，通过从前一个子集 中删除最小的索引来创建每个子集 。这些子集所使用的海森矩阵的逆 可以在 的各行共享（下文的图 2 更直观地说明了这一点）。关键的是，[2] 提出了一种通过 高效计算 的方法，只需通过高斯消元法消去对应的行和列，时间复杂度为 ：

图 2 展示了具体的权重重建的流程：对 及其对应的海森矩阵的逆 按照掩码的列进行有序迭代，如果 ，则对该行的 进行修剪（图像的白色），并更新这些行中位于被处理列的“右侧”的其余权重（图中的深蓝色）。

▲ 图2. SparseGPT 重建算法的可视化流程

2.4 计算复杂度

由 2.3 节的流程可将近似重建过程分为三个部分：（a）初始海森矩阵的计算，时间复杂度为 ， 是样本数量；（b）初始海森矩阵逆的计算，时间复杂度为 ；（c）迭代重建过程，计算集中在式（7）的高斯消元法上，共需要迭代 次，因此总时间复杂度为 。整体的时间复杂度为 ，因此 2.1 节的预期目标已经实现，整体的时间复杂度降低了一个数量级，这使得即使在 GPT 这样的大模型上该算法也可以实际应用。

自适应掩码选择

第 2 节只考虑了权重重建过程（算法的计算量主要也集中于此）。对于掩码选择阶段，常见的方法是利用某种重要性指标来选取掩码，例如 AdaPrune [1]。然而，最近的工作 [2] 表明，在修剪过程中更新权重会导致重要性的显著变化，如果能在掩码选择阶段考虑这一影响将获得更准确的结果。因此 SparseGPT 设计了一种能在权重重建过程中自适应选择掩码的方法。

最直接的做法是在每一列中利用 OBS/OPU 选择最容易修剪的 的权重，这将带来 的整体稀疏率。但这种方法存在一个巨大的缺陷，即稀疏性不能在列之间非均匀分布，这会导致非结构化剪枝的性能下降。对于 GPT 大模型来说，这一问题更为明显，[2] 中有研究表明 GPT 大模型在早期层中存在大量死亡的 ReLU，这导致很多列可以全部被去除，列之间的稀疏性存在极大差异。

为了平衡精度和计算成本，SparseGPT 将通过分块迭代求解来实现自适应地掩码选择，图 3 很好地展示了这一平衡策略——以 个列为一组进行分块的掩码选择，每块内保持 的稀疏率，再确定好掩码后，按照图 3 的重建算法流程对该块及右侧的列进行权重补偿。

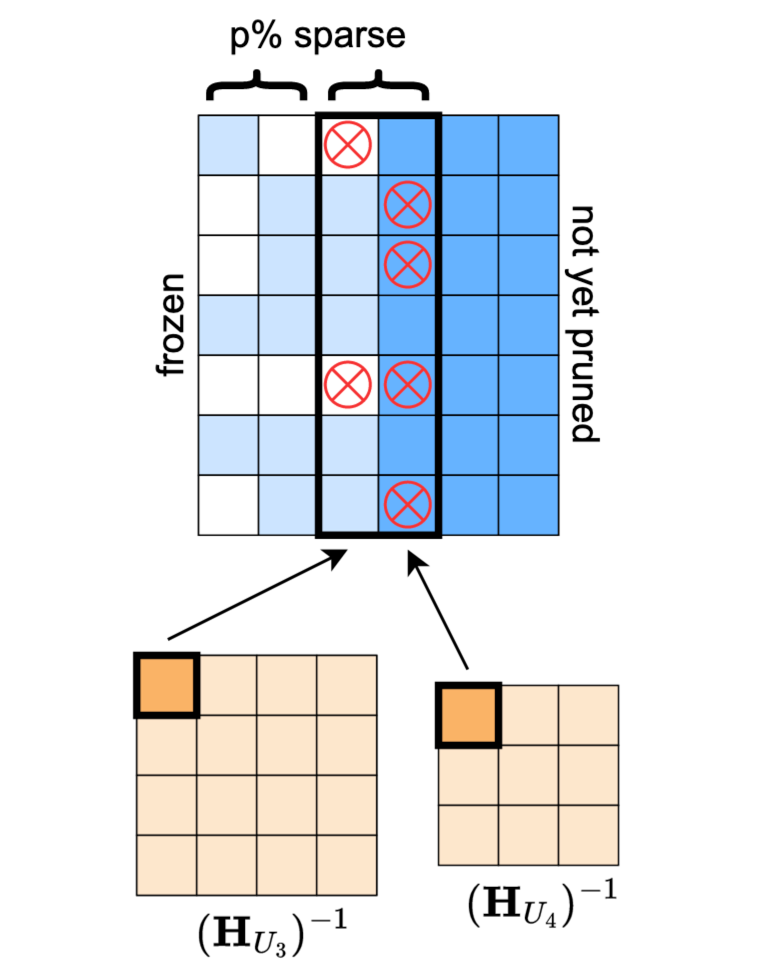
▲ 图3. 自适应掩码选择策略

半结构化稀疏扩展：图 3 的掩码选择策略很容易适应半结构化剪枝模式，以 Ampere NVIDIA GPU 上适用 2:4 稀疏格式为例，该模式要求在每个连续的 个权重中应该包含 个零。我们只需要将分块的列数量 ，并根据式（5）选择使误差最小的 个权重即可。

实验

1. 不同模型尺寸的剪枝表现：表 1 给出了不同剪枝策略在不同模型大小上的性能表现。幅值剪枝仅在稀疏 10% 时保持较为良好的精度，而 SparseGPT 可以在稀疏 50~60% 的情况下保持精度不变。在 OPT-175B 上，SparseGPT 稀疏 50% 参数量的情况下，性能反而更好，困惑度从 8.34 降低至 8.21（越低越好）。同时 4:8 或 2:4 的半结构化剪枝扩展也有着良好的性能表现，这些方法能够在硬件上获得实际的推理加速和内存占用减少。

▲ 表1. OPT 在 raw-WikiText2 数据集上的困惑度结果

2. Zero-shot 实验：在表 2 中，作者还补充了几个 Zero-shot 任务中 OPT-175B 的各种稀疏变体的结果。从中可以看出稀疏 50% 的 SparseGPT 几乎与原始模型有着相同的零样本识别能力。

▲ 表2. OPT-175B的稀疏变体在多个数据集上的 Zero-shot 结果表现

参考文献

[1] Itay Hubara, Brian Chmiel, Moshe Island, Ron Banner, Seffi Naor, and Daniel Soudry. Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks. In Conference on Neural Information Processing Systems (NeurIPS), 2021.

[2] Elias Frantar, Sidak Pal Singh, and Dan Alistarh. Optimal Brain Compression: A framework for accurate post-training quantization and pruning. arXiv preprint arXiv:2208.11580, 2022. Accepted to NeurIPS 2022, to appear.

[3] Thomas Blumensath and Mike E Davies. Iterative thresholding for sparse approximations. Journal of Fourier Analysis and Applications, 14(5-6):629–654, 2008.

[4] Babak Hassibi, David G Stork, and Gregory J Wolff. Optimal brain surgeon and general network pruning. InIEEE International Conference on Neural Networks, 1993.

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·

本文链接：https://my.lmcjl.com/post/10397.html