❓ 116. 填充每个节点的下一个右侧节点指针
难度:中等
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

示例 2:
提示:
- 树中节点的数量在 [ 0 , 2 12 − 1 ] [0, 2^{12} - 1] [0,212−1] 范围内
- − 1000 < = n o d e . v a l < = 1000 -1000 <= node.val <= 1000 −1000<=node.val<=1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
💡思路:前序遍历(递归)
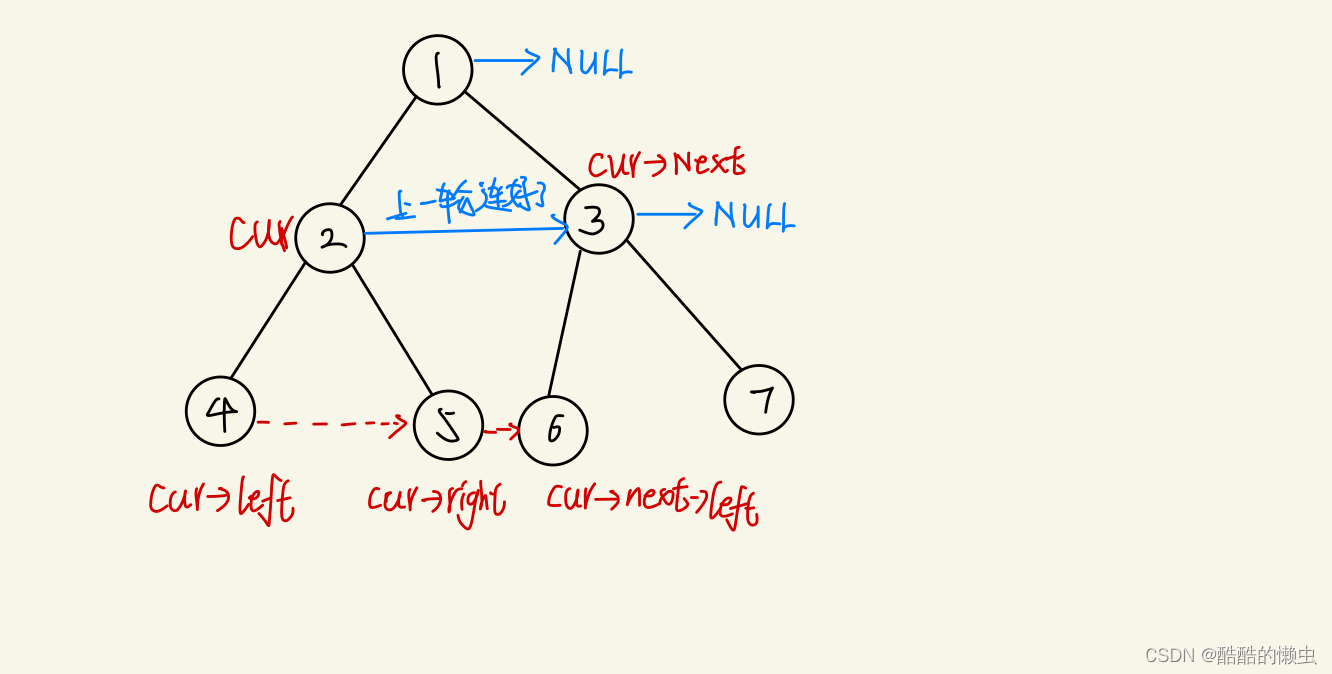
假如当前操作的节点是 cur:
- 最关键的点是可以通过上一层递归 搭出来的线,进行本次搭线。
🍁代码:(Java、C++)
Java
/*
// Definition for a Node.
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
*/class Solution {private void traversal(Node cur){if(cur == null) return;if(cur.left != null) cur.left.next = cur.right;if(cur.right != null) {if(cur.next != null) cur.right.next = cur.next.left;else cur.right.next = null;}traversal(cur.left);traversal(cur.right);}public Node connect(Node root) {traversal(root);return root;}
}
C++
/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
private:void traversal(Node* cur){if(cur == nullptr) return;if(cur->left != nullptr) cur->left->next = cur->right;if(cur->right != nullptr){if(cur->next != nullptr) cur->right->next = cur->next->left;else cur->right->next = nullptr;}traversal(cur->left);traversal(cur->right);}
public:Node* connect(Node* root) {traversal(root);return root;}
};
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),每个节点只访问一次。
- 空间复杂度: O ( 1 ) O(1) O(1),不需要存储额外的节点。
题目来源:力扣。
注: 如有不足,欢迎指正!
本文链接:https://my.lmcjl.com/post/1041.html
展开阅读全文

4 评论