目录

• 说明
• Tensor
• • Tensor的创建
  • Tensor（张量）基本数据类型与常用属性
  • Tensor的自动微分
  • • 设置不可积分计算
• pytorch 计算图
• • backward一些细节

该文章解决问题如下：

• 对于tensor计算梯度，需设置requires_grad=True
• 为什么需要tensor.zero_grad()
• tensor.backward()中两个参数gradient 和retain_graph介绍

说明

在pytorch旧版本中有两个基本对象：Tensor（张量），Variable（变量）。其中tensor不能进行反向传播；Variable是一种不断变化的类型，符合参数更新的属性，因此可以反向传播。

其实Variable是对tensor的一种封装，操作和tensor基本一致，但是每个Variable都多了三个属性

• .data: tensor本身的数据
• .grad: 对应tensor的梯度
• .grad_fn: 获得.grad的方式（这个可能不是很好理解，后面有说明。表示该tensor的梯度值的计算来自于哪，如果没有，则是None。这里可以简单类比于函数中的自变量和因变量，如果是自变量，那么该属性值就是None；如果是因变量，其梯度来自于其自变量的计算）

每次创建了tensor张量，如果需要计算梯度，需要先将其转换为Variable变量后计算，并且属性requires_grad要设置为True。

from torch.autograd import Variable
import torch# 创建一个torch.Size([2, 3])的tensor
x_tensor = torch.randn(2, 3)# 将tensor封装成Variable类型，用于计算梯度，这里的requires_grad要设置为True
x = Variable(x_tensor, requires_grad=True)y = 3 * x ** 2 + 1print(y.type())  # torch.FloatTensor
print(y.grad_fn)  # <AddBackward0 object at 0x0000021679AB9700># 梯度参数grad_variables形状必须与Variable一致
grad_variables = torch.FloatTensor([[1, 2, 3],[1, 1, 1]])# 求函数y对x的梯度，这里需要输入参数，否则会报错grad can be implicitly created only for scalar outputs
y.backward(grad_variables)
print(x.grad)  # 得到x的梯度

在新版本的pytorch中，torch.autograd.Variable 和torch.Tensor同属于一类。以下所有的都是操作都是在新版本的pytorch下执行的。

Tensor

Tensor的创建

Tensor是n维的数组，在概念上与numpy数组是一样的，不同的是Tensor可以跟踪计算图和计算梯度。其创建可以来自于python的内置数据类型，也可以来自于其他（numpy）等。以下给出几种创建tensor的方法：

import torch
import numpy as np# 从numpy中创建
numpy_array = np.array([2, 1, 2])
torch_tensor1 = torch.from_numpy(numpy_array)
torch_tensor2 = torch.Tensor(numpy_array)
torch_tensor3 = torch.tensor(numpy_array)# 将tensor转换回numpy类型
numpy_array = torch_tensor1.numpy()  # 如果tensor在CPU上
numpy_array = torch_tensor1.cpu.numpy()  # 如果tensor在GPU上
print(type(numpy_array))  # 输出 ： <class 'numpy.ndarray'>

# 创建形状为size的全为fill_value的Tensor
a = torch.full(size=[2, 3], fill_value=2)
# 创建形状为size的全为1的Tensor
b = torch.ones(size=[2, 3])
# 创建形状为size的全0的Tensor
c = torch.zeros(size=[2, 3])
# 创建对角阵的Tensor
d = torch.eye(3)
# 在区间[low,high]中随机创建形状为size的Tensor
e = torch.randint(low=1, high=10, size=[2, 2])

在使用torch.Tensor()方法创建Tensor的时候可以设置数据类型（dtype）与设备（device）

a = torch.tensor(data=[[1, 3, 1], # 数据[4, 5, 4]],dtype=torch.float64,# 数据类型device=torch.device('cuda:0')) # 设备# 可以通过Tensor的属性查看
print(a.dtype)  # torch.float64
print(a.device)  # cuda:0
print(a.is_cuda)  # True

在使用tensor的时候，如果将tensor放在GPU中，则可以加速tensor的计算。

# 1,定义cuda数据类型
# 把Tensor转换为cuda数据类型
dtype = torch.cuda.FloatTensor
gpu_tensor = torch.tensor(data=[[1, 3, 1],[4, 5, 4]]).type(dtype)# 2.直接将Tensor放到GPU上
a = torch.tensor(data=[[1, 3, 1],[4, 5, 4]])
gpu_tensor = a.cuda(0)  # 把Tensor直接放在第一个GPU上
gpu_tensor = a.cuda(1)  # 把Tensor直接放在第二个GPU上# 如果将GPU上tensor放回CPU也简单
a_cpu = gpu_tensor.cpu()

Tensor（张量）基本数据类型与常用属性

Tensor的最基本数据类型：

• 32位浮点型：torch.float32 (最常用）
• 64位浮点型：torch.float64 (最常用）
• 32位整型：torch.int32
• 16位整型：torch.int16
• 64位整型：torch.int64

a.type 可以重新生成一个数据类型的相同数据的tensor。

import torch# 创建一个tensor
a = torch.tensor(data=[[1, 3, 1],[4, 5, 4]])
# 查看Tensor类型
print(a.dtype)  # torch.int64# 如果不传入参数，则默认转换为torch.LongTensor类型
b = a.type(torch.float64)
print(a.dtype)  # torch.int64
print(b.dtype)  # torch.float64# 查看Tensor尺寸
print(a.shape)  # torch.Size([2, 3])# 查看Tensor是否在GPU上
print(a.is_cuda)  # False# 查看Tensor存储设备
print(a.device)  # cpu# 查看Tensor梯度计算，如果没有，则是None
print(a.grad)  # None# 如果要计算梯度，requires_grad需要设置为True
print(a.requires_grad)  # False

Tensor的自动微分

将Torch.Tensor的requires_grad 属性设置为True，那么pytorch将开始跟踪对此张量的所有操作。完成计算后，可以调用.backward()方法自动计算所有梯度。并且该张量的梯度计算值将累加到.grad属性中。

• .data: tensor本身的数据
• .grad: 对应张量的梯度累加和
• .grad_fn: 获得.grad的方式（来自于什么函数，如果是自己创建的，则是None）

# 创建tensor
x = torch.tensor(data=[[1, 2],[2, 1]],dtype=torch.float64,requires_grad=True)
print(x.requires_grad)  # Truey = x ** 2 + 2
y = y.mean()# 在计算backward的时候，y必须是标量，否则需要设置一下backward函数的输入参数。
y.backward()
print(x.grad)
"""
tensor([[0.5000, 1.0000],[1.0000, 0.5000]], dtype=torch.float64)
"""

但是这里有个问题，由于梯度是累加到.grad中的，如果存在多个函数对同一个数据x求解梯度，其梯度是累加之和。可以通过Tensor.grad.data.zero_()对.grad进行清零操作。

# 创建tensor
x = torch.tensor(data=[[1, 2],[2, 1]],dtype=torch.float64,requires_grad=True)
print(x.requires_grad)  # Truez = 4 * x + 2
z = z.mean()z.backward()
print(x.grad)
"""
tensor([[1., 1.],[1., 1.]], dtype=torch.float64)
"""# 对x的梯度清0操作，否则会由于x的不同梯度进行叠加操作。
# x.grad.data.zero_()y = x ** 2 + 2
y = y.mean()# 在计算backward的时候，y必须是标量，否则需要设置一下backward函数的输入参数。
y.backward()
print(x.grad)
"""
tensor([[1.5000, 2.0000],[2.0000, 1.5000]], dtype=torch.float64)
"""

设置不可积分计算

有时候不需要去跟踪计算。例如，用于测试集的测试数据（全设置为不跟踪计算），或者冻结权重信息（一部分跟踪计算）。

实现该方法的原理是将不需要计算梯度的tensor的.requires_grad属性设置为False即可。

改变Tensor（张量）变量的requires_grad值语句：

# 就地改变Tensor变量a的requires_grad属性为True
a.requires_grad = True 
a.requires_grad_(True)  # 与上面等价，注意下划线

用于测试集，使用with torch.no_grad(),在该模块下的所有计算得出的tensor的.requires_grad属性将自动设置为False。

import torchx = torch.randn(3, 4, requires_grad=True)
y = torch.randn(3, 4, requires_grad=True)u = x + y
print(u.requires_grad)  # True
print(u.grad_fn)  # <AddBackward0 object at 0x000001D0DC709700>with torch.no_grad():w = x + yprint(w.requires_grad)  # Falseprint(w.grad_fn)  # None
print(w.requires_grad)  # False

用于冻结权重，对网络中参数进行遍历，将需要冻结参数的tensor设置为True，其他设置为False

# 遍历模型权重信息
for name, para in model.named_parameters():# 按照名字将其进行冻结,这里冻结最后一层的fc，和fc.biasif "fc" not in name and "fc.bias" not in name:para.requires_grad_(False)

pytorch 计算图

计算图是用来描述运算的有向无环图，主要由结点（Node）和边（Edge）构成，其中结点表示数据，而边表示运算。

以 y = f ( x 1 , x 2 , x 3 , x 4 ) = ( x 1 + x 2 ) ( x 2 − x 3 − x 4 ) y=f\left( x_1,x_2,x_3,x_4 \right) =(x_{1}+x_{2})(x_{2} - x_{3}-x_{4}) y=f(x1​,x2​,x3​,x4​)=(x1​+x2​)(x2​−x3​−x4​) 为例, 其计算图如下图所示，其中 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1​,x2​,x3​,x4​ 为叶子节点。

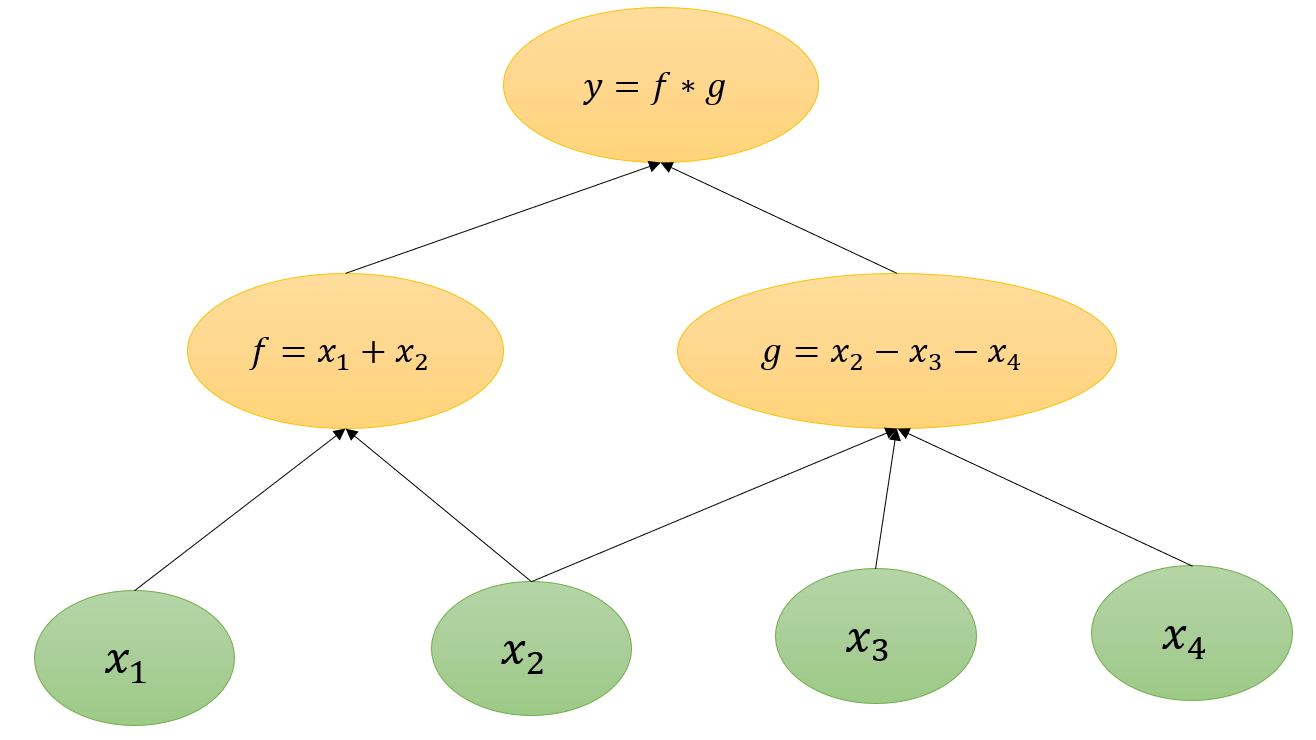
由链式法则，可以知道，如果要计算某个叶子结点对其根结点的导数，就是根结点到该叶子结点所有路径上的导数求和。（也进一步说明为什么.grad是累加的。）

import torch# 创建tensor
x_1 = torch.tensor(data=[1.], requires_grad=True)
x_2 = torch.tensor(data=[2.], requires_grad=True)
x_3 = torch.tensor(data=[3.], requires_grad=True)
x_4 = torch.tensor(data=[4.], requires_grad=True)f = x_1 + x_2
g = x_2 - x_3 - x_4y = f * g
# y.retain_grad()y.backward()
print(x_2.grad)# 查看叶子结点
print(x_1.is_leaf, x_2.is_leaf, x_3.is_leaf, x_4.is_leaf, f.is_leaf, g.is_leaf, y.is_leaf)
# 输出：True True True True False False False# 查看梯度
print(x_1.grad, x_2.grad, x_3.grad, x_4.grad, f.grad, g.grad, y.grad)
# 输出：tensor([-5.]) tensor([-2.]) tensor([-3.]) tensor([-3.]) None None None

在torch.tensor中有个属性is_leaf属性用于指示张量是否为叶子结点。叶子节点是整个计算图的根基，无论是求导计算图还是反向传播过程中，所有的梯度计算都依赖于叶子结点。设置叶子节点主要是为了节省内存，在梯度反向传播结束之后，非叶子节点的梯度都会被释放掉。

backward一些细节

形式：

tensor.backward(gradient, retain_graph)

pytoch构建的计算图是动态图，为了节约内存，所以每次一轮迭代完之后计算图就被在内存释放。如果使用多次backward就会报错。可以通过设置标识retain_graph=True来保存计算图，使其不被释放。

import torchx = torch.randn(4, 4, requires_grad=True)
y = 3 * x + 2
y = torch.sum(y)y.backward(retain_graph=True)  # 添加retain_graph=True标识，让计算图不被立即释放
y.backward()  # 不报错
y.backward()  # 报错

还有，以上所有的计算梯度都是基于y是标量的情况下，如果不是标量的情况下，需要对backward传入参数gradient 也就是说当y不再是标量，而是多维张量的情况下，需要设置gradient。那么为什么需要使用该参数，并且该参数如何使用？

这里举个例子，设， Y = [ y 1 y 2 ] Y=\left[ \begin{array}{c} y_1\\ y_2\\ \end{array} \right] Y=[y1​y2​​]， W = [ w 11 w 12 w 21 w 22 ] W=\left[ \begin{matrix} w_{11}& w_{12}\\ w_{21}& w_{22}\\ \end{matrix} \right] W=[w11​w21​​w12​w22​​]， X = [ x 1 x 2 ] X=\left[ \begin{array}{c} x_1\\ x_2\\ \end{array} \right] X=[x1​x2​​]，且满足： Y = W X , A = f ( Y ) Y=WX, A=f(Y) Y=WX,A=f(Y)，其中，函数 f ( y 1 , y 2 ) f(y_1,y_2) f(y1​,y2​)的具体定义未知。
[ y 1 y 2 ] = [ w 11 w 12 w 21 w 22 ] [ x 1 x 2 ] A = f ( y 1 , y 2 ) \left[ \begin{array}{c} y_1\\ y_2\\ \end{array} \right] =\left[ \begin{matrix} w_{11}& w_{12}\\ w_{21}& w_{22}\\ \end{matrix} \right] \left[ \begin{array}{c} x_1\\ x_2\\ \end{array} \right] \\ A = f(y_1,y_2) [y1​y2​​]=[w11​w21​​w12​w22​​][x1​x2​​]A=f(y1​,y2​)
改成标量形式：
y 1 = w 11 x 1 + w 12 x 2 y 2 = w 21 x 1 + w 22 x 2 A = f ( y 1 , y 2 ) y_1=w_{11}x_1+w_{12}x_2 \\ y_2=w_{21}x_1+w_{22}x_2 \\ A = f(y_1,y_2) y1​=w11​x1​+w12​x2​y2​=w21​x1​+w22​x2​A=f(y1​,y2​)
基于此，我们需要计算出 A A A 对 x 1 , x 2 x_1,x_2 x1​,x2​的偏导，即需要求解 ∂ A ∂ x 1 \frac{\partial A}{\partial x_1} ∂x1​∂A​ 和 ∂ A ∂ x 2 \frac{\partial A}{\partial x_2} ∂x2​∂A​，根据复合函数链式求解法则，有
∂ A ∂ x 1 = ∂ A ∂ y 1 ∂ y 1 ∂ x 1 + ∂ A ∂ y 2 ∂ y 2 ∂ x 1 ∂ A ∂ x 2 = ∂ A ∂ y 1 ∂ y 1 ∂ x 2 + ∂ A ∂ y 2 ∂ y 2 ∂ x 2 \begin{aligned} \frac{\partial A}{\partial x_1}&=\frac{\partial A}{\partial y_1}\frac{\partial y_1}{\partial x_1}+\frac{\partial A}{\partial y_2}\frac{\partial y_2}{\partial x_1}\\ \frac{\partial A}{\partial x_2}&=\frac{\partial A}{\partial y_1}\frac{\partial y_1}{\partial x_2}+\frac{\partial A}{\partial y_2}\frac{\partial y_2}{\partial x_2}\\ \end{aligned} ∂x1​∂A​∂x2​∂A​​=∂y1​∂A​∂x1​∂y1​​+∂y2​∂A​∂x1​∂y2​​=∂y1​∂A​∂x2​∂y1​​+∂y2​∂A​∂x2​∂y2​​​
上面 2个等式可以写成矩阵相乘的形式，如下:
[ ∂ A ∂ x 1 , ∂ A ∂ x 2 ] = [ ∂ A ∂ y 1 , ∂ A ∂ y 2 ] [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ] \left[ \frac{\partial A}{\partial x_1},\frac{\partial A}{\partial x_2} \right] =\left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2} \right] \left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}\\ \end{matrix} \right] [∂x1​∂A​,∂x2​∂A​]=[∂y1​∂A​,∂y2​∂A​][∂x1​∂y1​​∂x1​∂y2​​​∂x2​∂y1​​∂x2​∂y2​​​]
其中
[ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ] \left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}\\ \end{matrix} \right] [∂x1​∂y1​​∂x1​∂y2​​​∂x2​∂y1​​∂x2​∂y2​​​]
叫作雅可比( Jacobian) 式。雅可比式可以根据已知条件求出。
现在只要知道 [ ∂ A ∂ y 1 , ∂ A ∂ y 2 ] \left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2} \right] [∂y1​∂A​,∂y2​∂A​] 的值哪怕不知道 f ( y 1 , y 2 ) f\left(y_1, y_2\right) f(y1​,y2​) 的具体形式也能求出来 [ ∂ A ∂ y 1 , ∂ A ∂ y 2 ] \left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2} \right] [∂y1​∂A​,∂y2​∂A​] 。 那现在的问题是怎么样才能求出 [ ∂ A ∂ y 1 , ∂ A ∂ y 2 ] \left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2} \right] [∂y1​∂A​,∂y2​∂A​]

该部分由pytorch的backward函数中的gradient参数提供。

这里提供一种计算方式，设 W = [ 1 2 3 4 ] W=\left[ \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right] W=[13​24​]，则雅可比( Jacobian) 式为 [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ] = [ 1 2 3 4 ] \left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}\\ \end{matrix} \right] = \left[ \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right] [∂x1​∂y1​​∂x1​∂y2​​​∂x2​∂y1​​∂x2​∂y2​​​]=[13​24​] （这里凑巧等于W了，而且该雅可比的计算和 x 1 , x 2 x_1,x_2 x1​,x2​无关，在其他情况下不一定这么凑巧）。

于是无论 x 1 , x 2 x_1,x_2 x1​,x2​ 取何值，其雅可比式固定，然后通过gradient传入参数torch.tensor([0.1, 0.2], dtype=torch.float)即：
[ ∂ A ∂ x 1 , ∂ A ∂ x 2 ] = [ ∂ A ∂ y 1 , ∂ A ∂ y 2 ] [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ] = [ 0.1 , 0.2 ] [ 1 2 3 4 ] = [ 0.7 , 1.0 ] \left[ \frac{\partial A}{\partial x_1},\frac{\partial A}{\partial x_2} \right] =\left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2} \right] \left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}\\ \end{matrix} \right] =\left[ 0.1,0.2 \right] \left[ \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right] =\left[ 0.7,1.0 \right] [∂x1​∂A​,∂x2​∂A​]=[∂y1​∂A​,∂y2​∂A​][∂x1​∂y1​​∂x1​∂y2​​​∂x2​∂y1​​∂x2​∂y2​​​]=[0.1,0.2][13​24​]=[0.7,1.0]
代码实现如下：

# 在实现的时候，取了巧，所以计算的梯度和理论上存在转置
import torchx = torch.tensor(data=[[1], [2]], dtype=torch.float64, requires_grad=True)  # 定义一个输入变量w = torch.tensor([[1, 2],[3, 4]], dtype=torch.float64)y = torch.mm(w, x)  # 矩阵相乘
y.backward(gradient=torch.FloatTensor([[0.1], [0.2]]))
print(x.grad.data)# 输出：
"""
tensor([[0.7000],[1.0000]], dtype=torch.float64)
"""

当然，这里以一个三维的输入和输出例子举例：
y 1 = x 1 + x 2 − x 3 y 2 = x 1 x 2 + x 3 y 3 = x 1 − x 2 x 3 A = f ( y 1 , y 2 , y 3 ) \begin{gathered} y_1=x_1 + x_2- x_3 \\ y_2=x_1x_2+x_3 \\ y_3=x_1-x_2 x_3 \\ A=f\left(y_1, y_2, y_3\right) \end{gathered} y1​=x1​+x2​−x3​y2​=x1​x2​+x3​y3​=x1​−x2​x3​A=f(y1​,y2​,y3​)​
那么其多元复合函数求导的矩阵形式如下：
[ ∂ A ∂ x 1 , ∂ A ∂ x 2 , ∂ A ∂ x 3 ] = [ ∂ A ∂ y 1 , ∂ A ∂ y 2 , ∂ A ∂ y 3 ] [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 1 ∂ x 3 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ∂ y 2 ∂ x 3 ∂ y 3 ∂ x 1 ∂ y 3 ∂ x 2 ∂ y 3 ∂ x 3 ] \left[\frac{\partial A}{\partial x_1}, \frac{\partial A}{\partial x_2}, \frac{\partial A}{\partial x_3}\right]=\left[\frac{\partial A}{\partial y_1}, \frac{\partial A}{\partial y_2}, \frac{\partial A}{\partial y_3}\right]\left[\begin{array}{lll} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \frac{\partial y_1}{\partial x_3} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \frac{\partial y_2}{\partial x_3} \\ \frac{\partial y_3}{\partial x_1} & \frac{\partial y_3}{\partial x_2} & \frac{\partial y_3}{\partial x_3} \end{array}\right] [∂x1​∂A​,∂x2​∂A​,∂x3​∂A​]=[∂y1​∂A​,∂y2​∂A​,∂y3​∂A​]⎣⎢⎡​∂x1​∂y1​​∂x1​∂y2​​∂x1​∂y3​​​∂x2​∂y1​​∂x2​∂y2​​∂x2​∂y3​​​∂x3​∂y1​​∂x3​∂y2​​∂x3​∂y3​​​⎦⎥⎤​
假设传入gradient参数为torch.tensor([0.1, 0.2, 0.3], dtype=torch.float)，并且假定 x 1 = 1 , x 2 = 2. x 3 = 3 x_1=1,x_2=2.x_3=3 x1​=1,x2​=2.x3​=3，理论上的梯度有：
[ ∂ A ∂ x 1 , ∂ A ∂ x 2 , ∂ A ∂ x 3 ] = [ ∂ A ∂ y 1 , ∂ A ∂ y 2 , ∂ A ∂ y 3 ] [ 1 1 1 x 2 x 1 1 1 − x 3 − x 2 ] = [ 0.1 , 0.2 , 0.3 ] [ 1 1 1 2 1 1 1 − 3 − 2 ] = [ 0.8 , − 0.6 , − 0.3 ] \left[ \frac{\partial A}{\partial x_1},\frac{\partial A}{\partial x_2},\frac{\partial A}{\partial x_3} \right] =\left[ \frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2},\frac{\partial A}{\partial y_3} \right] \left[ \begin{matrix} 1& 1& 1\\ x_2& x_1& 1\\ 1& -x_3& -x_2\\ \end{matrix} \right] =\left[ 0.1,0.2,0.3 \right] \left[ \begin{matrix} 1& 1& 1\\ 2& 1& 1\\ 1& -3& -2\\ \end{matrix} \right] =\left[ 0.8,-0.6,-0.3 \right] [∂x1​∂A​,∂x2​∂A​,∂x3​∂A​]=[∂y1​∂A​,∂y2​∂A​,∂y3​∂A​]⎣⎡​1x2​1​1x1​−x3​​11−x2​​⎦⎤​=[0.1,0.2,0.3]⎣⎡​121​11−3​11−2​⎦⎤​=[0.8,−0.6,−0.3]
对应代码如下：

import torchx = torch.tensor([1, 2, 3], requires_grad=True, dtype=torch.float)y = torch.randn(3)y[0] = x[0] + x[1] + x[2]
y[1] = x[0] * x[1] + x[2]
y[2] = x[0] - x[1] * x[2]y.backward(torch.tensor([0.1, 0.2, 0.3], dtype=torch.float))print(x.grad)
# 输出：
"""
tensor([ 0.8000, -0.6000, -0.3000])
"""

本文链接：https://my.lmcjl.com/post/11860.html