目录 

P25思考与练习1

【补充作业题1】

P30思考练习题2

【补充作业题2】

P33思考练习题3

P33综合练习题

P25思考与练习1

1.一维数组访问。
1）在subjects数组中选择并显示序号1、2、4门课的名称，使用倒序索引选择并显示names数组中“方绮雯”。
2）选择并显示names数组从2到最后的数组元素：选择并显示subjects数组正序2~4的数组元素。
3）使用布尔条件选择并显示subjects数组中的英语和物理科目名称。

#1，一维数组访问
import numpy as np
#注：names写在subjects前面表示names作为行索引，subjects作为列索引。即谁写在前面谁做二位数组的行索引。
names = np.array(['王微','肖良英','方绮雯','刘旭阳','钱易铭'])        
subjects = np.array(['Math','English','Python','Chinese','Art','Database','Physics'])#1）
print(subjects[[1,2,4]])
print(names[-3])#2)
print(names[2: ])
print(subjects[2:5])#3)
print(subjects[(subjects == 'English')|(subjects =='Physics')])      

2.二维数组访问。
1）选择并显示scores数组的1、4行。
2）选择并显示scores数组中行序2、4学生的数学和Python成绩。
3）选择并显示scores数组中所有学生的数学和艺术课程成绩。
4）选择并显示scores数组中“王微”和“刘旭阳”的英语和艺术课程成绩。

#2.二维数组访问
import numpy as np
scores = np.array([[70,85,77,90,82,84,89],[60,64,80,75,80,92,90],[90,93,88,87,86,90,91],[80,82,91,88,83,86,80],[88,72,78,90,91,73,80]])
print(scores)#1)
print(scores[[1,4]])#2)
print(scores[[2,4]][: ,(subjects == 'Math')|(subjects == 'Python')])#3)
print(scores[: ,(subjects == 'Math')|(subjects == 'Art')])#4)
print(scores[(names == '王微')|(names == '刘旭阳')][: ,(subjects == 'English')|(subjects == 'Art')])

3.生成由整数10~19组成的2×5的二维数组。

#方法一
import numpy as np
b = np.arange(10,20).reshape(2,5)    #arange（）函数生成10~19的10个连续整数
print(b)#方法二
c = np.random.randint(10,20,size = (2,5))    #randint()函数生成10~19的10个随机整数
print(c)

【补充作业题1】

1. 创建一维数组a，数组元素是6个整数，10, 20，30,  40,  50,  0
2. 选取并显示索引序号为0的数组元素
3.  选取数组a中，索引为1~ 3的数组元素
4.  使用条件筛选，选出数组中值大于20的元素
5.  使用条件筛选，选出数组中值大于等于20并且小于50的元素
6. 修改索引序号为2的数组元素的值，新值为1000
7.  将索引序号为-1 的数组元素的值，减去10

import numpy as np
#第1题
a = np.array([10,20,30,40,50,0])#第2题
print(a[0])#第3题
a[1:4]
print(a[1:4])#第4题
a[a>20]
print(a[a>20])#第5题
a[(a>=20)&(a<50)]            
print(a[(a>=20)&(a<50)])#第6题
a[2] = 1000
print(a)#第7题
a[-1]-10
print(a[-1]-10)

P30思考练习题2

1,将scores数组中所有学生的英语成绩减去3分并显示。

2.统计scores数组中每名学生所有科目的平均分并显示。

3,使用随机函数生成[-1,1]之间服从均匀分布的3×4二维数组，并计算所有元素的和。

#思考与练习2
import numpy as np
names=np.array(['王薇','肖良英','方绮雯','刘旭阳','钱易铭'])
subjects=np.array(['Math','English','Python','Chinese','Art','Database','Physics'])
scores=np.array([[70,85,77,90,82,84,89],[60,64,80,75,80,92,90],[90,93,88,87,86,90,91],[80,82,91,88,83,86,80],[88,72,78,90,91,73,80]])
#1
a = scores[: ,subjects =='English']-3
print(a)#2
b = scores.mean(axis = 1)
print("每位同学的所有科目的平均分为：")
for i in range(0,5):print(names[i],":",b[i])#3
b = np.random.uniform(-1,1,size = (3,4))     #uniform()函数的生成的随机数范围，两端都取。此题中可取-1与1。
print(b)
print(b.sum())

【补充作业题2】

1.选取scores中第2行第2列元素

scores[1,1]

2.选取scores中两个元素，行序号为0，列序号为1的元素；以及行序号为3，列序号为6的元素。

scores[[0,3],[1,6]]

3.选取数组scores中的前3行数据

#方法一
scores[0:3]        #或scores[0:3,: ]#方法二
scores[[0,1,2]]    #或scores[[0,1,2],: ]

4.选取scores中，列序号为1~4 的列

#方法一：
scores[: ,1:5]                 #或scores[: ,[1,2,3,4]]或scores[[0,1,2,3,4],1:5]或scores[0:5,1:5]#方法二
scores[[0,1,2,3,4]][: ,1:5]    #或scores[[0,1,2,3,4]][: ,[1,2,3,4]]#方法三
scores[0:5][: ,1:5]            #或scores[: ,][: ,1:5]或scores[: ,: ][: ,1:5]或scores[: ,: ][: ,[1,2,3,4]]

5.选取scores中，行序号为1,2，列序号为0,2,4 的元素

#方法一
scores[1:3,[0,2,4]]#方法二：两层切片，先行后列
scores[1:3][: ,[0,2,4]]      #或scores[[1,2]][: ,[0,2,4]] #方法三：两层切片，先列后行
scores[: ,[0,2,4]][1:3]      #或scores[: ,[0,2,4]][[1,2]]

6.选取钱易铭的成绩

scores[(names == '钱易铭')]#for循环输出成绩
m = scores[(names == '钱易铭')]
print("钱易铭各科目的成绩为：")
for i in range(0,7):print(subjects[i],":",m[0,i])

7.选取钱易铭的数学成绩

scores[(names == '钱易铭'),(subjects =='Math')]

8.选取王薇和肖良英的数学和英语成绩

#方法一：双层切片，先行（人名）后列（学科）
scores[(names =='王薇')|(names =='肖良英')][: ,(subjects == 'Math')|(subjects =='English')]#方法二：双层切片，先列（学科）后行（人名）
scores[: ,(subjects == 'Math')|(subjects =='English')][(names =='王薇')|(names =='肖良英')]

9.选取scores中，大于等于80并且小于90的元素

scores[(scores>=80)&(scores<90)]

10.将第1列元素的值都增加5

#单独显示增加5的那一列
#方法一：
scores[: ,0]+5#方法二：采用函数,subtract()减函数与add()加和函数
np.subtract(scores[: ,0],-5)
np.add(scores[: ,0],5)#方法三：构造ones()函数
a = np.ones((1,5))*5   
scores[: ,0]+a
#或者
b = np.ones((5,1))*5       
scores[: ,0]+b.T              #用到了数组的转置#方法四：构造zero()函数
c = np.zeros((5,7))
c[: ,0] = 5
scores+c #显示全部列
#方法一：
scores+[5,0,0,0,0,0,0]#方法二：采用ones()函数
m = np.zeros((5,7))
m[: ,0] = 5
scores+m#方法三：
n = np.ones((5,7))*5
n[: ,1: ] =0#或者c[: ,1:7]=0
scores+n

P33思考练习题3

1.将随机游走的步数增加到100步，计算物体最终与原点的距离。

#第1题
#模拟每步生成方向
import numpy as np
steps = 100
rndwlk = np.random.randint(0,2,size = (2,steps))
rndwlk = np.where(rndwlk>0,1,-1)
print(rndwlk)
#计算每步移动后的位置
position = rndwlk.cumsum(axis = 1)                #按行累加求和
print(position)
#计算每步移动后与原点的距离
dists = np.sqrt(position[0]**2+position[1]**2)    #sqrt求平方根
print(dists)
print(round(dists[-1],4))                         #格式化输出保留4位小数。round（数，保留位数）

2.重复多次随机游走过程，观察物体与原点距离的变化趋势。 

【探索一】：

import numpy as np
l = []
for i in range(100):                                  #循环100次，步数为100steps = 100rndwlk = np.random.randint(0,2,size = (2,steps))rndwlk = np.where(rndwlk>0,1,-1)position = rndwlk.cumsum(axis = 1)                #按行累加求和dists = np.sqrt(position[0]**2+position[1]**2)    #sqrt求平方根np.set_printoptions(precision =4)l.append(dists)
m = np.array(l)             #将l转化为二维数组
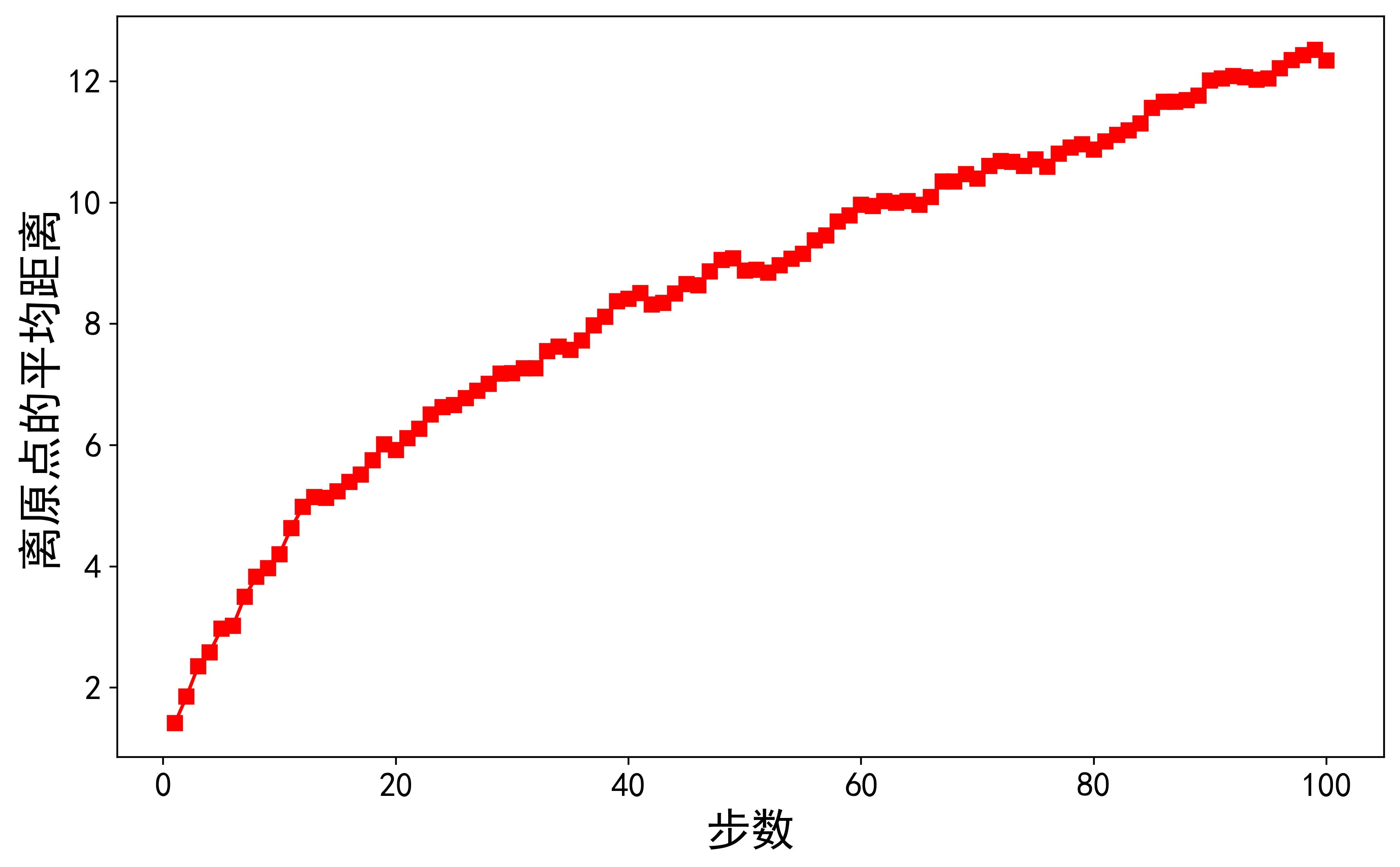
y =m.mean(axis = 0)         #使用mean（）函数对二维数组按列求均值，计算每一步到原点的平均距离
print(m.shape)              #查看物体走100次100步每一步距离得到的二维数组的行列数
print('每一步到原点的平均距离：',y)#使用matplotlib画图
import matplotlib.pyplot as plt
plt.figure(figsize = (10,6))                 #设置画布大小
plt.rcParams['font.sans-serif']=['SimHei']   #显示中文
plt.rcParams['axes.unicode_minus']=Falsex = np.arange(1,101)                       #arange（）函数得到1~100连续的整数，作为以下画折线图的横坐标
plt.plot(x,y,marker = 's',color = 'r')     #plt.plot画折线图，marker设置标记点的形状，颜色为红色（缩写为r）
plt.xticks(fontsize = 15)                  #设置横坐标刻度大小
plt.yticks(fontsize =15)                   #设置纵坐标刻度大小
plt.xlabel('步数',fontsize = 20)           #增加横坐标标签
plt.ylabel('离原点的平均距离',fontsize = 20) #增加纵坐标标签
plt.show()                                    #显示图像

100次：

1000次：

10000次：

【探索二】：

运行100次： 

import numpy as np
l = []
for i in range(100):steps = 100rndwlk = np.random.randint(0,2,size = (2,steps))rndwlk = np.where(rndwlk>0,1,-1)position = rndwlk.cumsum(axis = 1)                dists = np.sqrt(position[0]**2+position[1]**2)   l.append(round(dists[-1],2))
print(l)
print("物体走100步后离原点的平均距离：",np.array(l).mean())          #将1列表转为数组，利用mean（）函数求均值#使用matplotlib绘制散点图，分析趋势
import matplotlib.pyplot as plt
plt.figure(figsize = (20,6))                                       #定义图形大小
plt.scatter(x = np.arange(1,101),y = l,marker = '*',c = 'red')    #plt.scatter()函数画散点图
plt.show()                                                         #展示图形#根据散点图分析，建立回归分析模型
x = np.arange(1,101).astype(float)                               #astype()函数强制类型转换为浮点型
Y = np.array(l)                                                    #将l列表转为数组
from sklearn.linear_model import LinearRegression                  
linreg = LinearRegression()                                        #初始化模型
linreg.fit(x.reshape(-1,1),Y)                                      #添加.reshape(-1,1)解决x单独一行/列不为二维数组出错的问题
print(linreg.intercept_,linreg.coef_)                              #输出回归模型截距，回归系数

结果 ：

运行100次，

物体走100步后离原点的平均距离：12.9684

其中一次运行得到的次数与距离的回归方程：y = -0.0067x+13.31

散点图如下：

 运行1000次：

结果 ：

物体走100步后离原点的平均距离：12.6370

其中一次运行得到的次数与距离的回归方程：y = 0.0008x+12.24

散点图如下：

运行10000次： 

结果 ：

物体走100步后离原点的平均距离：12.5448

其中一次运行得到的次数与距离的回归方程：y = 3.5381e-5x+12.37

散点图如下：

P33综合练习题

1.“大润发”、“沃尔玛”、“好德”和“农工商”四个超市都卖苹果、香蕉、橘子和芒果四种水果。使用NumPy的ndarray实现以下功能。
1）创建两个一维数组分别存储超市名称和水果名称。
2）创建一个4×4的二维数组存储不同超市的水果价格，其中价格由4~10范围内的随机数生成。
3）选择“大润发”的苹果和“好德”的香蕉，并将价格增加1元。
4）“农工商”水果大减价，所有水果价格减2元。
5）统计四个超市节果和芒果的销售均价。
6）找出橘子价格最贵的超市名称（不是编号）。

#综合练习题1
#1）
import numpy as np
names = np.array(['大润发','沃尔玛','好德','农工商'])      #names在前，即names作为二维数组的行索引
fruits = np.array(['苹果','香蕉','橘子','芒果'])           #fruits在后，即fruits作为二维数组的列索引#2）
price = np.random.randint(4,11,size = (4,5))               #采用random模块的randint（）函数，生成4~10的随机整数
print(price)#3）
a = price[(names == '大润发')|(names =='好德'),(fruits == '苹果')|(fruits == '香蕉')]+1
print(a)#4）
b= price[names == '农工商']-2
print(b)#5）
c = price[: ,(fruits =='苹果')|(fruits =='芒果')].mean(axis = 0)       #axis = 0,按列处理。axis = 1，按行处理。
print(c)#6)
d = price[: ,fruits =='橘子'].argmax()                                 #argmax（）求最大值的索引
print(names[d])

2.基于2.3节中随机游走的例子，使用ndarray和随机数生成函数模拟一个物体在三准空间随机游走的过程。
1）创建3×10的二维数组，记录物体每步在三个轴向上的移动距离。在每个轴向的移动距离服从标准正态分布(期望为0，方差为1)。行序0、1、2分别对应x轴、y轴和z轴。
2）计算每步走完后物体在三维空间的位置。
3）计算每步走完后物体到原点的距离（只显示两位小数）。
4）统计物体在z轴上到达的最远距离。
5）统计物体在三维空间距离原点的最近值。
【提示】使用abs( )绝对值函数对z轴每步运动后的位置求绝对值，然后求最大距离。

#2三维空间随机游走
import numpy as np
#1）
movedists = np.random.normal(0,1,size = (3,10))        #random模块下的normal（）函数生成x、y、z轴上三组正态分布随机数
print(movedists)#2）
position = movedists.cumsum(axis = 1)                  #按行求累加和，计算每步走后的x、y与z轴的坐标位置
print(position)#3)
dists = np.sqrt(position[0]**2+position[1]**2+position[2]**2)   #根据每步位置坐标计算到原点的距离，用到sqrt（）求平方根函数
np.set_printoptions(precision=2)                                #np.set_printoptions()函数设置显示的小数位数
print(dists)#4)
print(np.abs(position[2]).max())                                #abs（）绝对值函数#5)
print(dists.min())   

【拓展——补充】：接综合练习题第2题，绘图展示物体三维空间游走轨迹

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D   #调用Axes3D库
plt.rcParams['font.sans-serif']=['SimHei']   #显示中文
plt.rcParams['axes.unicode_minus']=False
x = position[0]   #表示位置参数
y = position[1]
z = position[2]
fig = plt.figure(figsize = (12,8))    #创建绘图对象，figsize定义图形大小
ax = plt.axes(projection='3d')        #创建三维坐标轴
ax.set_xlabel('X轴',fontsize = 15)   #以下三行分别设置x轴、y轴与z轴标题与字号大小
ax.set_ylabel('Y轴',fontsize = 15)
ax.set_zlabel('Z轴',fontsize = 15)
ax.set_title( '物体在三维空间上一次随机游走轨迹图',fontsize = 20)   #添加标题，设置字号
ax.plot(x,y,z,c = 'g',marker = '*')    #画折线图
ax.scatter(0,0,0,c = 'b',marker = 'D')   #单独画原点
ax.text(.1,-.1,.1,'origin',fontsize = 15)   #添加原点说明文字
ax.scatter(x[0],y[0],z[0],c = 'r',marker = 'o')   #单独画起点
ax.text(x[0]+.1,y[0]-.1,z[0]+.1,'start',fontsize = 15)   #添加起点说明文字
ax.scatter(x[-1],y[-1],z[-1],c = 'r',marker = 'o')   #单独画终点
ax.text(x[-1]+.1,y[-1]-.1,z[-1]+.1, 'stop',fontsize = 15)   #添加终点说明文字
plt.show()   #显示图

运行结果如下：

本文链接：https://my.lmcjl.com/post/12003.html