| 实验目的: 1. 掌握多元数据的相关性、正态性、可视化表征的基本原理; 2.熟悉掌握SPSS软件/R软件的基本用法和基本操作; 3.利用实验指导中及软件中内置的实例数据,上机熟悉相关性检验+正态性检验+可视化数据方法。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验内容: 1.实验数据为女性汗液+ 32名学生核心课程成绩+R中iris数据+USairpolution; 2.分析变量之间的相关性,数据的正态性检验方法,解释结果; 3.利用SPSS或者R软件绘制均值条图、线图(带误差线)、箱式图(带误差线)、星象图、脸谱图等。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验前预习: 1.变量之间的相关性基本原理为,软件操作步骤; 2.数据正态性检验基本方法,操作步骤; 3.数据可视化方法操作步骤或者操作函数等。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 程序测试、运行结果及分析: 相关性
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“相关”à 选择“双变量” à 拖动算法和数分3至变量框 à 勾选“皮尔逊”和“双尾”(双尾表示两边进行显著性检验) à 点击确定 运行结果:
结果分析: 由结果显示算法和数分3的皮尔逊相关系数为0.453介于0.4和0.6之间,所以相关程度为中等,sig(双尾)为0.009,也就是在0.01级别p值为0.009小于0.05,所以显著相关性。
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“相关” à 选择“偏相关” à 拖动高代1和数分1至变量框 à 拖动数分1至控制框 à 点击“选项”勾选“零阶相关性” à 勾选 “双尾”(双尾表示两边进行显著性检验) à 点击”继续”和“确定” 运行结果:
结果分析: 在没有控制变量(数分1)的影响下,高代1和高代2的相关系数为0.576,相关程度为中等,p值为0.001小于0.05具有显著相关性。在有控制变量(数分1)的影响下高代1和高代2相关系数为0.072,相关程度极低,p值为0.669大于0.05说明没有显著相关性。 数据正态性检验基本方法 方法一:Q-Q图和P-P图检验: 操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“描述统计” à 选择“Q-Q图”或者“p-p图” à 拖动c语言至变量框 à 检验分布选择“正态” à 点击“确定”
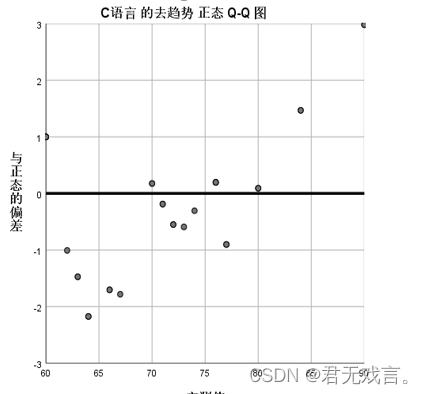
Q-Q图就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图其斜率为标准差,截距为均值,由图形可知,在60到70之间的数据绝大多数都偏离正态分布,所以c语言不符合正态分布。 p-p图就是由标准正态分布的累积比例为横坐标,样本值的累积比例为纵坐标的散点图,同Q-Q图的分析,60到70的样本数据偏离正态分布的标准值,所以我们认为c语言不服从正态分布。
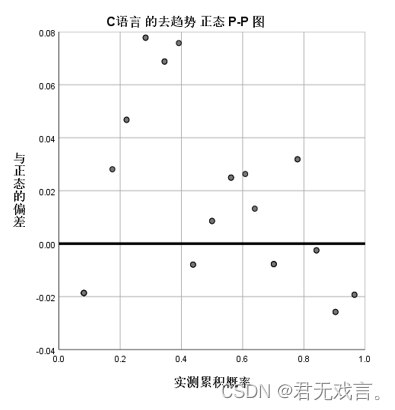
c语言的去趋势正态Q-Q图用于表示各个数据的残差,由上图可知,在70到80之间的数据残差的绝对值均比其他数据小,如果将70到80的数据拿出检验其正态性,一定比剩余数据好。但此样本的残差绝对值绝大数大于0.05,所以我们认为c语言不符合正态分布。 由图可知0.2到0.4之间的数据与标准线的距离较大并且大于0.05,表明样本数据的离散程度在累计比例0.2到0.4的区间最大,也就成绩在60到70之间的数据离散程度最大,所以我们认为c语言不服从正态分布
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“描述统计” à 选择“描述” à 拖动c语言至变量框 à 点击“选项”à 勾选“峰度”和“偏度”à 点击“确定” 运行结果:
结果分析: c语言的偏度为0.500,说明该数据为正偏态,表示数据左端有较多的极端值,数据均值左侧的离散程度强。也就时上面所分析的60到70之间的数据离散程度大。峰度为-0.470,而完全服从正态分布的数据的峰度值时3。无论偏度和峰度都偏离标准的正态分布过多,所以c语言不符合正态分布。
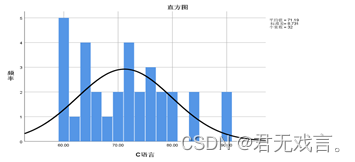
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“描述统计” à 选择“频率” à 拖动c语言至变量框 à 点击“选项”à 点击“图表”à 勾选“直在直方图中显示正态曲线” à 点击“继续”和“确定” 运行结果:
结果分析: 由图可知,直方图的左边由许多极端值,所以c语言数据不符合正态分布。
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“非参数检验” à 选择“旧对话框” à 点击“单样本K-S” à 拖动数分1至变量框 à 点击“选项” à 勾选“描述”和“四分位数” à 点击“继续”和“确定” 运行结果:
结果分析: 表格中渐进显著性(双尾)为0小于0.05,则拒绝原假设(服从正态分布),认为数分1的数据不服从正态分布。
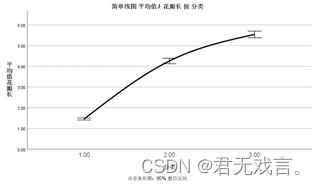
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“图形”à 点击“图表构建器” à 在图库栏点击“折线图”à 双击第一个简单线图à 拖动花瓣长至y轴,不同种类的分类拖动至x轴à 在元素属性框点击“折线图” à 在统计框选择“平均值”à勾选下方“显示误差条形图”à在插值框类型选择为“样条”à点击“确定” 运行结果:
结果分析: 由图形可知第3类品种的花瓣普遍比其他两类的长,花瓣最短的是第1类花的花瓣。
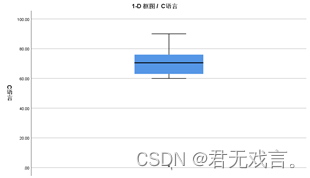
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“图形”à 点击“图表构建器” à 在图库栏点击“箱图” à 双击最后一个1-D框图形式的箱图à 拖动c语言至右侧x轴 à 点击“确定” 运行结果:
结果分析: 为了方便分析,我把c语言的第一个数据改成了1,由图形显示可以看出出现了一个下标为1的星形点,说明了这个第一个数据偏离总数据,视为异常值,分析的时候可以剔除。
操作步骤: 打开r软件,在输入框输入install.packages("caret"),按回车出现对话框,选择china(beijing 2)[https],点击确定,等待加载。分别录入加载包library(caret),library(ggplot2),library(lattice),install.packages("aplpack"),library(aplpack)在最后一行输入 data <- read.table("clipboard",header=T),不能按回车,在excel复制核心课程数据,再按回车,然后在r输入框内输入data点击回车,出现数据,输入stars(data),出现星象图 运行结果:
R语言实现 操作步骤: 打开r软件,在输入框输入install.packages("caret"),按回车出现对话框,选择china(beijing 2)[https],点击确定,等待加载。分别录入加载包library(caret),library(ggplot2),library(lattice),install.packages("aplpack"),library(aplpack)在最后一行输入 data <- read.table("clipboard",header=T),不能按回车,在excel复制32名学生核心课程成绩数据,再按回车,然后在r输入框内输入data点击回车,出现数据,输入faces(data),出现脸谱图。
结果分析: 1到32的序号分别代表2018级32名学生核心课程成绩的脸谱图,脸谱图是用来比较数据的,用于发现不同年级学生学习成绩数据的共性并进行分类。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 讨论: 1.变量之间的相关性基本原理 变量之间的相关性基本原理:研究两个变量之间的相关性原理,也就是研究当一个变量发生变化时,另外一个变量如何变化,所以只需要通过计算相关系数来做定量考察,相关系数R值越大说明两个变量越相关,反之相关程度越低,算出的p值如果大于0.05那么就接受原假设,反之拒绝原假设 有显著相关性。对于偏相关则指的是两变量同时与第三个变量相关时,把第三个变量的影响剔除,分析另外两个变量的相关过程,其基本原理与两变量相关性分析类似 2.数据正态性检验基本方法 方法一:正态曲线直方图。在分析选项卡下,选择描述--频率,在频率页面,在绘图选项选择带正态曲线的直方图。绘制带正态曲线的直方图通过对比直方图与正态曲线的拟合程度,判定数据序列的分布形态是否接近正态分布。 方法二:Q-Q图和P-P图。在分析选项卡下,选择“分析”-“描述统计”-“P-P图或Q-Q图”。P-P图与Q-Q图的判断原理相同,区别在于横纵坐标的单位不同,P是累积比例,Q是分位数。散点能够与斜线很好的吻合,则说明该数据序列符合正态分布,明显点分散在两侧,没有集中在一条直线上,不成正态分布。 方法四:峰度和偏度检验。偏度大于0表示正偏态,表示数据左端有较多的极端值,数据均值左侧的离散程度强。同理偏度小于0表示负偏态,表示数据右端有较多的极端值,数据均值右侧的离散程度强。偏度绝对值越大表示数据分布偏斜程度越大,所以偏度越接近于0其正态性越好,在用峰度和偏度对数据进行正态性检验时,除了要观察偏度是否在0附近,峰度是否在3附近之外,还需要满足以下要求:可以分别计算偏度和峰度的Z评分(Z-score),偏度Z-score = 偏度值/偏度标准差,以c语言的数据为例,其偏度Z-score=0.5/0.414=1.207,峰度Z-score = 峰度值/峰度值的标准差,同样以c语言的数据为例,峰度Z-score=-0.47/0.809=-0.58。
对于脸谱图:按照切尔诺夫于1973年提出的画法,脸谱图采用15个指标,各指标代表的面部特征为:1表示脸的范围,2表示脸的形状,3表示鼻子的长度,4表示嘴的位置,5表示笑容曲线,6表示嘴的宽度,7~11分别表示眼睛的位置、分开程度、角度、形状和宽度;12表示瞳孔的位置;,13~15分别表示眼眉的位置、角度和宽度。 对于箱线图:如果在箱图的上方或者下方出现点,说明该点为异常值,研究数据的时候可以剔除。(其他图较简单,在结果分析里已经详细说明,这里省略) |
本文链接:https://my.lmcjl.com/post/12539.html





4 评论