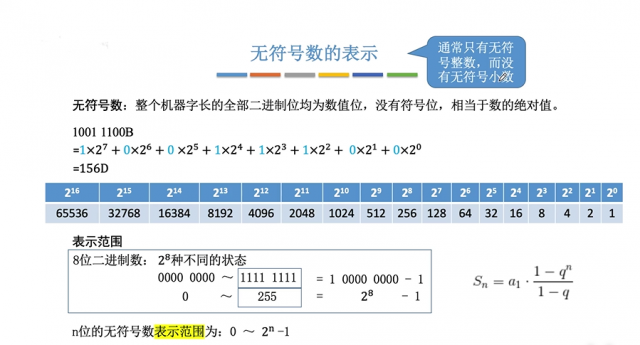
无符号数:
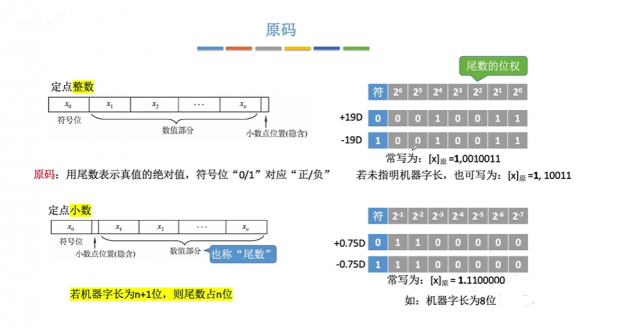
原码:
原码的数学定义:
若定点整数的原码形式为xn,xn-1,……x1,x0(xn为符号位)
当2n > x >= 0时,
[x]原 = x
当0 >= x > -2n时,
[x]原 = 2n - x = 2n + |x|
式中,[x]原是机器数,x是真值。
定点小数:
当1 > x >= 0时,
[x]原 = x
当 0 >= x > -1时,
[x]原 = 1 - x = 1 + |x|
例:十进制19.75可以表示成:
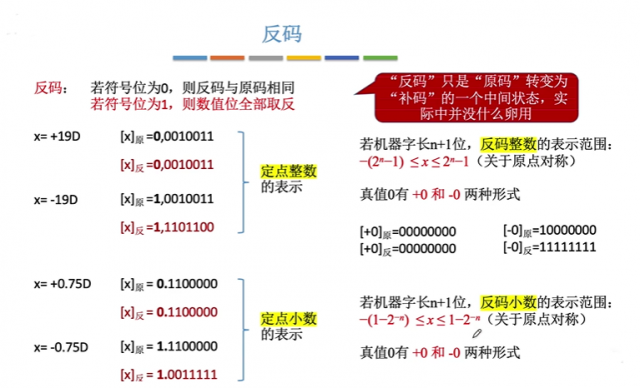
原码表示的范围:

反码:
(注意,整数为逗号,小数为点)
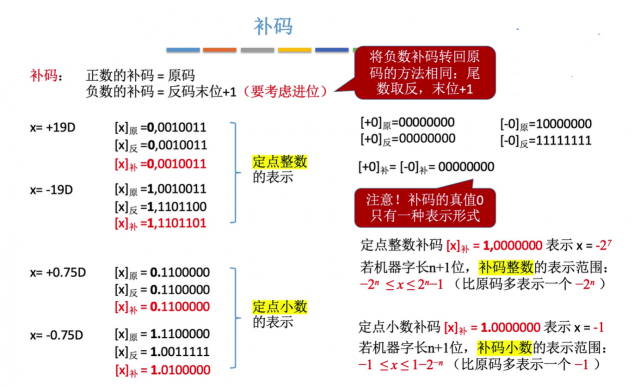
补码:
补码的数学定义:
若定点整数的原码形式为xn,xn-1,……x1,x0(xn为符号位)
当2n > x >= 0时,
[x]原 = x
当0>= x > -2n时,
[x]原 = 2n+1 + x = 2n+1 - |x|
式中,[x]原是机器数,x是真值。
定点小数:
当1 > x > 0时,
[x]原 = x
当 0 >= x >= -1时,
[x]原 = 2 + x = 2 - |x|

为什么正数补码是原码本身,而负数需要改变?
首先,整数的编码是先有最直观的非负数,然后再加上负数作为补充。补充负数的时候非负数的表达方法不能改变,这是很自然的。就如同硬件设计上都讲平稳退化一样。
其次,补码是完全的人为定义。正数的补码是其本身,这只是为了符合补码的设计原则:
任何两个补码直接二进制简单相加,即可得到正确运算结果并仍是补码。
比如一个字节长的无符号数的表示范围:
0~ 255,有符号数的表示范围:-128~ 127。应该这样来写:0~ 127~ -128~ -1,这才是较好的写法。为什么?因为这个写法的数的顺序与0~ 255一 一对应。
由上,我们了解,其实补码不过是用128~ 255这段范围的数来表示-128~-1这段范围的负数,而正数的部分没有发生改变。
那么就可以推测出计算补码的公式,就是:256 - 欲求的负数的绝对值 = 此负数的补码。
作用:
1.消除原码+0-0的矛盾,只存在0
2.方便计算机进行原码的减法运算(使用加法代替减法)
例:

负数的补码的为什么是原码取反再加一?
原因:a的绝对值 + a的补码 = 模(a为负数时)
例如,假设计算机的机器字长是8bit,二进制原码a为10001110,
数值位全部取反就是11110001,
a的绝对值为00001110,
a取反和a的绝对值两者相加的结果是11111111(2^8 - 1),
再加一就是100000000(2^8)(模)。’
例如,下面两个二进制数相加,当作为无符号数时可以轻松算出,但是,作为有符号数,而且加数还是个负数,因为CPU中只有加法器,所以计算机此时不知道该怎么运算减法了,就需要借助补码将负数转换成正数:
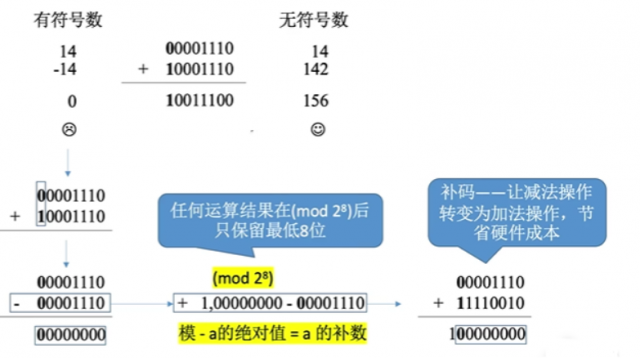
小技巧:

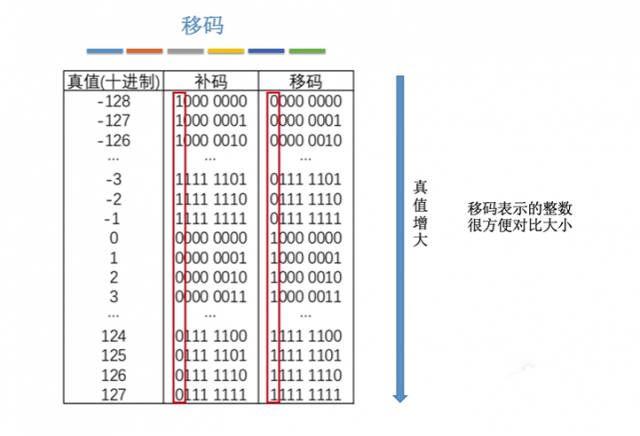
移码:
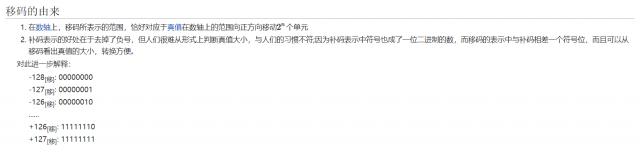
例如:8个机器字长的移码就是把所有的数字都加上 128,也就是把 -128 ~ +127 的范围的数字,都平移到 0 ~ 255 范围内,然后再用 0 ~ 255 的“机器数”来表示。
移码的定义:
当机器字长 = n + 1时:

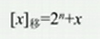
当机器字长 = n时:
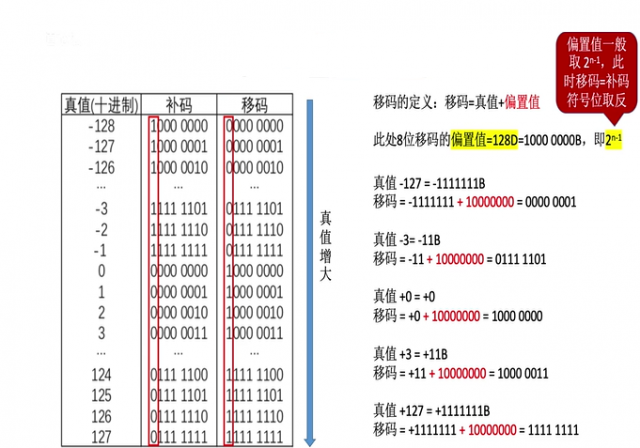

随着真值的增大,移码也是随之增大,因为这种特性,计算机可以通过这一点来比较两个数的大小,从最高位依次开始比较,哪一位先出现1,哪个数就比较大,所以也可以得出,移码全0最小,全1最大。(如果比较的两位都是1,则比较下一位。)
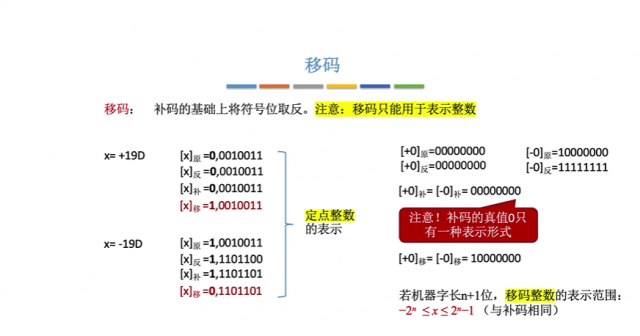
移码的特性:
移码有符号位。
移码的表示形式与补码相似,只是其符号位用“1”表示正数,用“0”表示负数,数值部分与补码相同。
总结例题:


本文链接:https://my.lmcjl.com/post/13511.html

4 评论