目录

前言

一、(十进制⇋n进制)进制转换详解

        1.先说说什么是进制

        2.二进制介绍

        3.(十进制⇋n进制)进制转换详解（重点)

                ①十进制 => n进制（2，8，16）

                ②n进制(2，8，16) => 十进制

                ③非十进制间的互相转化

二、原码、反码、移码，补码区别

        1.原码：

                优点：

                缺点：

        2.反码：

        3.移码：

        4.补码（重点）

        ΔPS : 负整数与二进制间的互相转换：

        5.八位二进制所代表的十进制示意图：

前言

        小伙伴儿大家好，这篇文章将会通俗易懂地给小伙伴儿们讲讲常见进制间相互转化，以及二进制的那些事儿。点击目录可以跳转，方便大家阅读，以后也可能进行补充或完善，感谢阅读。

一、(十进制⇋n进制)进制转换详解

        1.先说说什么是进制

        比方说，我们最常见的十进制，eg：1314，555，880，660，1800这些，只要是学过数学的，基本都见腻了，十进制就是个位十位百位千位......，不管你哪位都只能从0~9这十个数字中选一个，eg：330，个位是0，十位是3，百位也是3。每一位就一个数，而且只能从0~9里面挑，不能负数。

        所以，进制你可以理解为，n进制就是每位只能由规定的n个数来表示(即0 ~ n-1)，且每一位都可有n种表示，n个数中任挑一位。这里特别注意，16进制中，每一位是用0~15来表示，但为了形式整洁，从10开始用字母A表示，即10(A)，11(B)，12(C)，13(D)，14(E)，15(F)。

        PS（注意）：

        ①n进制每一位都是n种表示方法，所以，假设某n进制数共a位，那么一共可以表示n*n*n*n*n*....... = n 的 a次方 种可能。还是举个栗子比较直观:  十进制中的三位数，最高位是百位，它的个位可以是0~9中任意一个数，十位可以是0~9中任意一个数，百位可以是0~9中任意一个数，那么，一共就可以表示出10 的 3次方 = 1000个数，即(0 ~ 999)。

        ②在十进制中我们知道，个位的最小单位是1（10的0次方），十位的最小单位是10（10的1次方），百位的最小单位是100（10的二次方），再举个栗子：十进制中999，个位的9可以看作9 * 1，十位的9可以看作9 * 10，百位的9可以看作9 * 100。所以999 = (9*1) + (9*10) + (9*100)。

        --------->发现了什么规律没？最低位的最小单位是1，每往前一位，最小单位都扩大了十倍。那么推广到n进制：最低位仍是1，但每往前一位，规模都要扩大n倍，假设某n进制数共a位，那么它的最高位就是n 的 a-1 次方。或者说，十进制是满十进位，n进制就是满n进位。

        2.二进制介绍

        二进制，顾名思义，每一位都只能由两个数表示，0和1，以最简单的八位二进制（PS:计算机中最小的存储单元是位(bit)，1b就表示1位，八位即8b 表示一个字节(byte)，8b = 1byte)来演示：

        十进制中的1，八位二进制就是 0000 0001。其中，最高位表示符号位，0就是表示它是正数，-1表示它是负数。根据上面的结论我们可知，末尾的1就代表2 的 0次方，也就是1了，依次往前便是，2^1,2^2,2^3........一直到2 的 6次方，这时候可能有人会问：最高位不是n 的 a-1 次方吗，为啥不是2 的 7次方？这是因为八位二进制如果考虑到符号位，那么就剩下7位了，如果不考虑符号位，那么最高位必然是2 的 (8-1)次方，即2 的7次方，至于有符号位无符号位下，八位二进制分别能表示十进制中数字的什么范围，这个我们会在下面的进制转化详细解释，请耐心看下去。

        3.(十进制⇋n进制)进制转换详解（重点)

                ①十进制 => n进制（2，8，16）

                        //十进制转2进制

                这个简单，直接告诉你方法：（短除法) 除n取余，直至商0，余数倒序排列。

                老规矩，举个栗子直观点：比如，十进制185这个数，我们想把它转成2进制，我们只需要用短除法让185不停的除以2，每次运算都保留余数，直至商0，然后余数倒序排列，所得就是185对应的2进制形式。看这幅图片更加直观：

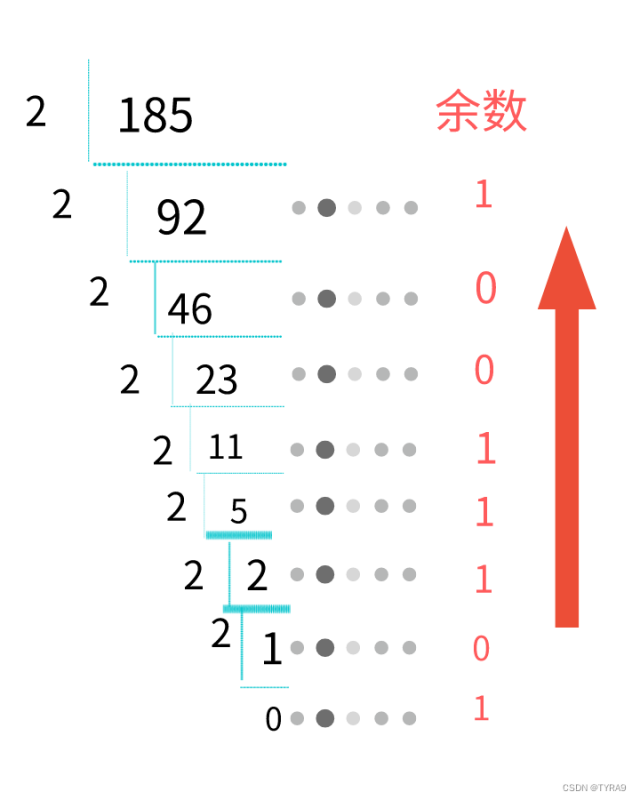
                那么，185对应的2进制形式就是10111001，即（185）10 = （10111001）2

                         //十进制转八进制

                例如，十进制185转为八进制，即使用短除法让185不停地除以8，保留余数，直至商0，然后把余数倒序排列即可。还是图片来得直观一些，

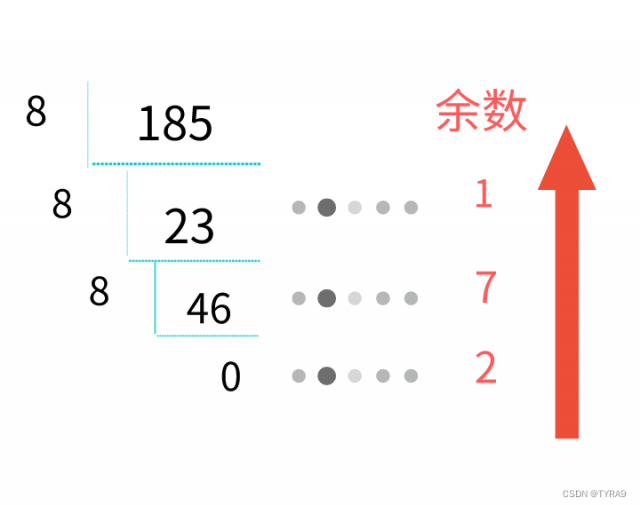                那么，185对应的8进制形式就是271，即（185）10 = （271）8

                          //十进制转十六进制

                例如，十进制3981转为十六进制，即使用短除法让3981不停地除以16，保留余数，直至商0，然后把余数倒序排列即可。还是图片来得直观一些，

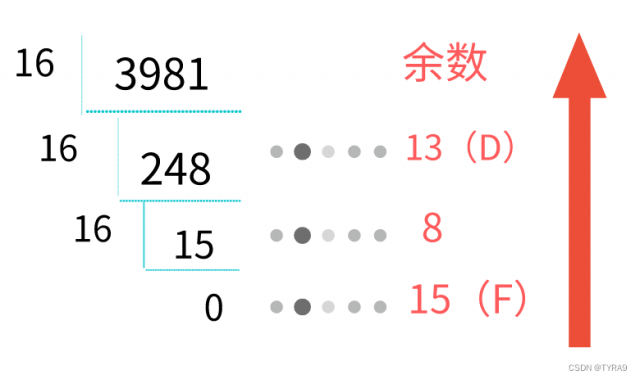
                那么，3981对应的8进制形式就是271，即（3981）10 = （F8D）16

                ②n进制(2，8，16) => 十进制

                         //2进制转为十进制

                前面我们说过，n进制：最低位仍是1，但每往前一位，规模都要扩大n倍，假设某n进制数共a位，那么它的最高位就是n 的 a-1 次方。因此，对应到2进制，就是最低位是1，每往前一位都要乘以2。

                我们还是以（无符号位）八位二进制 做演示，eg：00000011这个二进制怎么求十进制呢，很简单，最低位是1，以1（2的0次方）为最小单位，即1*1；次低位前的1以2（2的1次方）为最小单位，即1*2，然后我们把它们起来：1*1 + 1*2 = 3。所以这个二进制对应的十进制数就是3，即（00000011）2  =（3）10。

                由此我们得出2进制转十进制的方法就是：把每一位都转成十进制，然后把它们加起来。当然，此处仅限于首位是0的2进制，即对应于十进制中的正整数，负整数的求法在之后讲补码的时候会讲到。

                我们再来举个栗子 以加深印象：

                00011111这个2进制，转为十进制，即1*1 + 1*2 + 1*4 + 1*8 + 1*16 + 0*32 + 0*64 + 0*128 = 1+2+4+8+16 = 31;

                         // 8进制转为十进制

                8进制转为十进制与2进制完全同理，我们直接拿栗子来示范:

                eg1：(341) 8 = (1*1 + 4*8 + 3*64) 10 = (1+32+192) 10 = (225) 10。

                eg2：(1011) 8 = (1*1 + 1*8 + 0*64 + 1*512) 10 = (1+8+512) 10 = (521) 10。               

                         //16进制转为十进制

                16进制转为十进制与2进制，8进制完全同理，我们直接拿栗子来示范：

                eg1：(123) 16 = (3*1 + 2*16 + 1*256) 10 = (3+32+256) 10 = (291) 10。

                eg2：(11F) 16 = (15*1 + 1*16 + 1*256) 10 = (15+16+256) 10 = (287) 10。

                ③非十进制间的互相转化

                         //2进制转为8进制

                2进制转为8进制时，只需将2进制代码按照3位一组转成8进制即可，不够3位的左面补0。举个栗子：（注意，分组后独立，直接转就可以，不需要考虑它们之前什么地位）

                00110101，3位一组就可以分成（000）(这里补零了)，（110），（101），那么它们分别转化成8进制就是 (000) 2 = (0) 8，

                (110) 2 = (6) 8，  

                (101) 2 = (5) 8，

                最后把它们合起来就是（065）8，即（65）8。所以(00110101) 2 = (65) 8。

                        //2进制转为16进制

                2进制转为16进制，与2进制转为8进制类似，只不过是4位一组，不够4位的左面补零，老规矩，举个栗子：
                00101111，4位一组就可以分成（0010）（1111），那么它们分别转化成16进制就是

                (0010) 2 = (2) 16，

                (1111)  2 = (15) 16  =  (F) 16

                最后把它们合起来就是（2F）16，即(00101111)  2 = (2F) 16。

                PS：有小伙伴儿看到这里可能疑问重重，tnnd凭什么是3位和4位，你说是就是?

                        所以，为什么要把2进制分别拆分成三位一组或是四位一组呢？

        (⊙﹏⊙)呃，好问题! 这是因为2进制每一位都只有两种表示方法，而8进制，16进制每一位分别有三种，四种表示方法，所以你看，三位2进制有几种表示方法，2*2*2 = 8种（即0~7），正好！四位2进制有几种表示方法，2*2*2*2 = 16种（即0~15），正好！这不就是这么回事儿嘛

                PS：如果实在不会，可以用笨办法：即先转为十进制，再转为目标进制。

                         //16进制转为2进制，8进制转为2进制。

                直接将2进制转为16进制,2进制转为8进制的方法反过来即可 : 

                16进制转2进制，只需将每一个十六进制位转化为四个二进制位，最后按顺序合起来就可以。
                8进制转2进制， 只需将每一个八进制位转化为三个二进制位即可，最后按顺序和起来就可以。

                相当于上述栗子的逆过程，这里就不再赘述了，有问题可以在评论区提问。

                        ​​​​​​​//8进制和16进制之间能相互转化吗

                可以，但记住：不存在十六进制与八进制之间的直接相互转化，都是以二进制为中间进制来进行转化的。 

二、原码、反码、移码，补码区别

        ​​​​​​​        Δ首先要声明，原码反码移码补码这些，通通说的都是2进制。

        1.原码：

                        其实就是普通正常的二进制码，也叫"符号——绝对值“码 ，最高位是符号位，0表示正，1表示负，其余二进制位是该数字绝对值的二进制位。

                优点：

                                原码简单易懂

                缺点：

                                ①加减运算复杂，

                                ②存在加减乘除四种运算，增加了CPU的复杂度

                                ③零的表示不唯一(正负)

                                ④正负数不统一

        2.反码：

        ​​​​​​​        ​​​​​​​        正整数，原码 = 反码

                        负整数，反码  = 原码符号位不变，其余位全部取反，0变1，1变0

                        反码由于运算不便，实际也没有在计算机中应用

        3.移码：

                        移码表示数值平移n位，n称为移码量，移码主要运用于浮点数的阶码的存储。

                        说大白话就是，用的不多，了解一下即可

        4.补码：（重点）

                        真正的牛B，将正数和负数做到了统一，也是计算机实际的运算中所使用的。

                        正整数，原码 = 反码 = 补码。

                        负整数，补码 = 反码 + 1   (这里的+1 ，就是字面意思，最低位+1，满2就进位）

        ΔPS : 负整数与二进制间的互相转换：

                先说十进制转二进制 :       

                再来说说二进制转十进制 :       

        5.八位二进制所代表的十进制示意图：

                来一张八位二进制​​​​​​​所代表的十进制示意图：

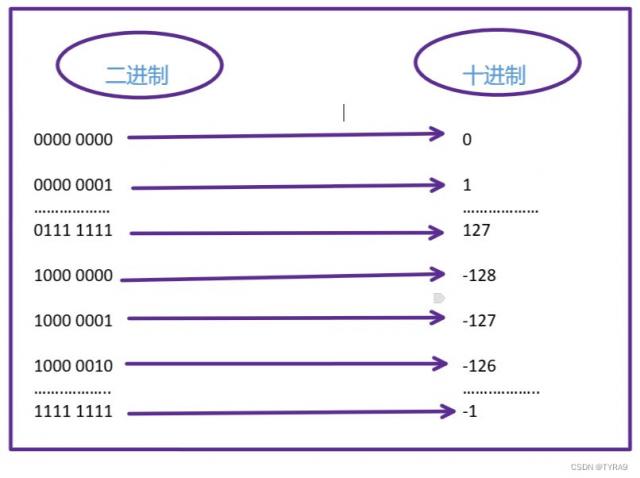
        这张图表也直观地表示出，有符号八位二进制所表示的十进制范围是:  -128 ~ 127

        小伙伴儿们若是还不熟悉，就把这张表的数挨个试试，熟能生巧。

System.out.println("END-------------------------------------------------");

本文链接：https://my.lmcjl.com/post/13546.html