基于spss的多元统计分析 之 实例3（血压、胆固醇于心脏病关系的研究）（8/8）

血压、胆固醇于心脏病关系的研究 摘要 一般线性模型中的一种，即反应变量 (dependent variables)为二分类变量的回归分析，模型输出为变量取特定值的概率。 在进行二元Logistic回归分析时，通常会涉及3个步骤，分别是数据处理、卡方分析和影响关系研究。     在研究相关因素对样本将来是否愿意购买理财产品的影响情况时，性别，专业等均为影响因素，而且明显的，性别和 0 Comments

血压、胆固醇于心脏病关系的研究

摘要

一般线性模型中的一种，即反应变量 (dependent variables)为二分类变量的回归分析，模型输出为变量取特定值的概率。
在进行二元Logistic回归分析时，通常会涉及3个步骤，分别是数据处理、卡方分析和影响关系研究。
    在研究相关因素对样本将来是否愿意购买理财产品的影响情况时，性别，专业等均为影响因素，而且明显的，性别和专业属于定类数据，因此需要进行虚拟哑变量设置，可使用【数据处理->生成变量】完成。
在进行二元logistic回归分析前，可先对X做差异分析，筛选出与Y有着差异性的X。
    二元Logistic回归分析时，首先需要看某个题是否呈现出显著性（如果P值小于0.05，则说明呈现出0.05水平的显著性；如果P值小于0.01，则说明呈现出0.01水平的显著性），如果呈现出显著性，那么说明该题对Y有影响关系。具体是正向影响还是负向影响需要结合对应的回归系数值进行说明，如果回归系数值大于0，则说明是正向影响；反之则说明是负向影响。

   

  • 实现步骤

第八题：

1.1在SPSS中输入数据

选择分析->回归->多元logistic

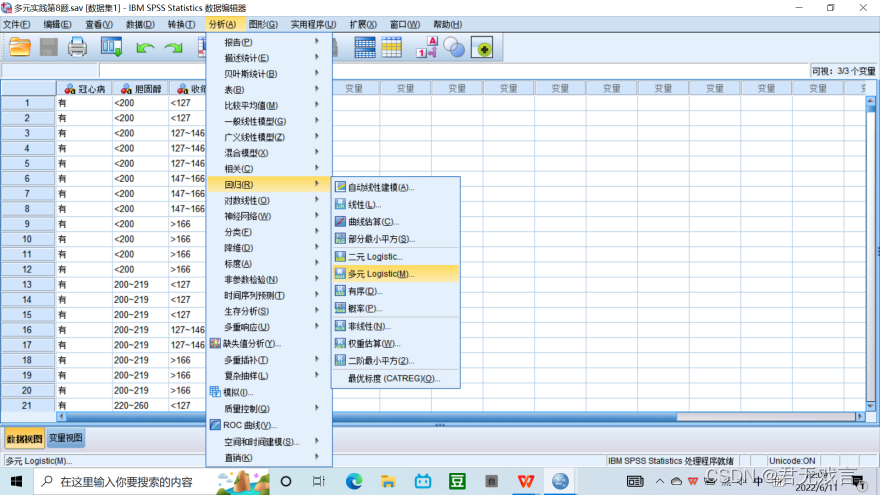
将冠心病选为因变量->将胆固醇、收缩压选为因子->确定

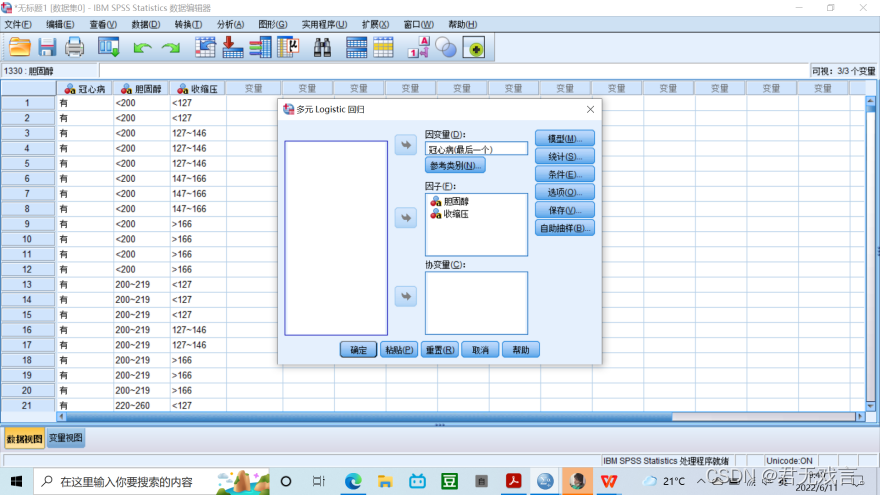
  • 结果分析

第八题：

个案处理摘要

 

个案数

边际百分比

冠心病

10

0.7%

无

1237

92.4%

有

92

6.9%

胆固醇

10

0.7%

<200

319

23.8%

>260

286

21.4%

200~219

254

19.0%

220~260

470

35.1%

收缩压

10

0.7%

<127

384

28.7%

>166

142

10.6%

127~146

579

43.2%

147~166

224

16.7%

有效

1339

100.0%

缺失

0

总计

1339

子群体

17a

a. 因变量在 2 (11.8%) 子群体中只有一个实测值。

结果显示，在1339名患者于健康人中，有10人其数据未知占比0.7%

模型拟合信息

模型

模型拟合条件

似然比检验

-2 对数似然

卡方

自由度

显著性

仅截距

228.556

最终

81.381

147.175

14

.000

P值小于0.05，说明拒绝原假设（不显著）出错的概率小，因此选择拒绝原假设，认为该模型显著

（假如模型不显著，则需要对模型进行调整即在似然比检验表格中挑选删除不显著效应再重新进行模型分析）

（拟合优度表格）

拟合优度越接近1，说明数据拟合越好，一般大于0.6（根据所需结果精度决定）

伪 R 方

考克斯-斯奈尔

.104

内戈尔科

.234

麦克法登

.187

对于多元logistic回归，伪R方表格参考意义不大，主要参考拟合优度表格。

似然比检验

效应

模型拟合条件

似然比检验

简化模型的 -2 对数似然

卡方

自由度

显著性

截距

81.381a

.000

0

.

胆固醇

101.276b

19.895

6

.003

收缩压

91.303b

9.922

6

.128

卡方统计是最终模型与简化模型之间的 -2 对数似然之差。简化模型是通过在最终模型中省略某个效应而形成。原假设是，该效应的所有参数均为 0。

a. 因为省略此效应并不会增加自由度，所以此简化模型相当于最终模型。

b. 在海森矩阵中遇到意外的奇异性。这表明应该排除某些预测变量或者合并某些类别。

由似然比检验表格可知，无论是胆固醇指数还是收缩压的数据对是否患病都有显著性影响

参数估算值

冠心病a

B

标准 错误

瓦尔德

自由度

显著性

Exp(B)

Exp(B) 的 95% 置信区间

下限

上限

截距

-3.439

1.508

5.199

1

.023

[胆固醇= ]

135.120

.000

.

1

.

4.806E+58

4.806E+58

4.806E+58

[胆固醇=<200]

.398

1.434

.077

1

.782

1.488

.090

24.742

[胆固醇=>260]

-1.041

1.496

.484

1

.486

.353

.019

6.627

[胆固醇=200~219]

.503

1.541

.107

1

.744

1.654

.081

33.906

[胆固醇=220~260]

0b

.

.

0

.

.

.

.

[收缩压= ]

0b

.

.

0

.

.

.

.

[收缩压=<127]

.359

1.657

.047

1

.829

1.432

.056

36.807

[收缩压=>166]

-1.072

2.178

.242

1

.623

.342

.005

24.442

[收缩压=127~146]

.587

1.543

.145

1

.704

1.798

.087

37.036

[收缩压=147~166]

0b

.

.

0

.

.

.

.

无

截距

2.371

.270

76.927

1

.000

[胆固醇= ]

.228

.000

.

1

.

1.256

1.256

1.256

[胆固醇=<200]

.427

.318

1.804

1

.179

1.533

.822

2.861

[胆固醇=>260]

-1.119

.236

22.561

1

.000

.327

.206

.518

[胆固醇=200~219]

.541

.354

2.331

1

.127

1.717

.858

3.437

[胆固醇=220~260]

0b

.

.

0

.

.

.

.

[收缩压= ]

0b

.

.

0

.

.

.

.

[收缩压=<127]

.386

.311

1.534

1

.216

1.470

.799

2.706

[收缩压=>166]

-1.151

.296

15.112

1

.000

.316

.177

.565

[收缩压=127~146]

.630

.284

4.937

1

.026

1.878

1.077

3.275

[收缩压=147~166]

0b

.

.

0

.

.

.

.

a. 参考类别为：^1。

b. 此参数冗余，因此设置为零。

首先观察显著列，挑选显著的行（即显著性值小于0.05，以黄底标注）

由此可以得出结论：当胆固醇大于等于260，收缩压大于等于166时对没有患冠心病有显著影响，所以自变量胆固醇和收缩压的范围分别为260到无穷，和166到无穷

  • 讨论

1.本质及类型Logistic回归其本质就是非线性回归，应用于检验因果关系或者预测

其有三种变量类型

二分类（判断有和无）

有序多分类（满意 基本满意 不满意）

无序多分类（坐飞机 坐火车 坐高铁）

2.Logistic回归原理（以二元Logistic为例）：研究的因变量y分为“是与否”两种可能，是一个二分类变量且仅取0和1两个值，p=P(y=1|x1，…，xk)是研究对象，它受k个因素x1，…，xk影响，则称为二元Logistic线性回归模型，简称Logistic回归模型，这k个因素x1，…，xk称为Logistic回归模型的协变量， 其概率公式为：

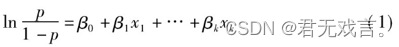
本文链接：https://my.lmcjl.com/post/1370.html

展开阅读全文

相关文章

4 评论

留下您的评论.