超参数指的是，比如各层的神经元数量、batch大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值，模型的性能就会很差。
那么如何能够高效地寻找超参数的值的方法

验证数据
之前我们使用的数据集分成了训练数据和测试数据，训练数据用于学习测试数据用于评估泛化能力。
下面要对超参数设置各种各样的值以进行验证。这里要注意的是不能使用测试数据评估超参数的性能。这一点非常重要，但也容易被忽视。为什么不能使用测试数据评估超参数的性能，因为如果使用测试数需调整超参数，超参数的值会对测试数据发生过拟合。

因此，调整超参数时，必须使用超参数专用的确认数据。用于调整超参也的数据，一般称为验证数据。一般使用这个验证数据评估超参数的好坏。

根据不同的数据集，有的会事先分成训练数据、验证数据、测试数据三部分，有的只分成训练数据和测试数据两部分，有的则不进行分割。如果是MNIST数据集，获得验证数据最简单的方法就是从训练数据中事先分割20%作为验证数据

(x_train, t_train),(x_test, t_test) = load_mnist()# 打乱训练数据
x_train, t_train = shuffle_dataset(x_train, t_train)# 分割验证数据
validation_rate = 0.28
validation_num = int(x_train.shape[0]*validation_rate)x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]

这里，分割训练数据前，先打乱了输人数据和监督标签。这是因为数据集的数据可能存在偏向（洗牌）

超参数的最优化
进行超参数的最优化时，逐渐缩小超参数的“好值”的存在范围非常重要。所谓逐渐缩小范围，是指一开始先大致设定一个范围，从这个范围中随机出一个超参数(采样)，用这个采样到的值进行识别精度的评估；然后，多重复该操作，观察识别精度的结果，根据这个结果缩小超参数的“好值”的范围通过重复这一操作，就可以逐渐确定超参数的合适范围。
（“好值”）

有报告叫显示，在进行神经网络的超参数的最优化时，与网格搜索等有规律的搜索相比，随机采样的搜索方式效果更好。这是因为在多个超参数中，各个超参数对最终的识别精度的影响程度不同。

超参数的范围只要“大致地指定”就可以了。所谓“大致地指定”，是指像0.001到1000这样，以“10的阶乘”的尺度指定范围

在超参数的最优化中，要注意的是深度学习需要很长时间。因此，在超参数的搜索中，需要尽早放弃那些不符合逻辑的超参数。于是，在超参数的最优化中，减少学习的epoch，缩短一次评估所需的时间是一个不错的办法。

下面简单归纳下：

1. 设定超参数的范围
2. 从设定的超参数范围中随机采样
3. 使用步骤1中采样到的超参数的值进行学习，通过验证数据评估识别精度(但是要将epoch设置得很小)
4. 重复步骤1和步骤2，根据它们的识别精度的结果，缩小超参数的范围

反复进行上述操作，不断缩小超参数的范围，在缩小到一定程度时，从施围中选出一个超参数的值。这就是进行超参数的最优化的一种方法

在参数的最优化中，如果需要更精炼的方法，可以使用贝叶斯最优化。贝叶斯最优化运用以贝叶斯定理为心的数学理论，能够更加严密、高效地进行最优化。

超参数最优化的实现
现在，我们使用MNIST数据集进行超参数的最优化。这里我们将学习率和控制权值衰减强度的系数(下文称为“权值衰减系数”)这两个超参数的搜索问题作为对象。

在该实验中，权值衰减系数的初始范围为10的负8次方到10的负4次方学习率的初始范围为10的负6次方到10的负2次方。此时，超参数的随机采样的代码如下所示：

weight_decay = 10 ** np.random.uniform(-8,-4)
lr = 10 ** np.random.uniform(-6,-2)

超参数最优化的源代码如下：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)# 为了实现高速化，减少训练数据
x_train = x_train[:500]
t_train = t_train[:500]# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]def __train(lr, weight_decay, epocs=50):network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],output_size=10, weight_decay_lambda=weight_decay)trainer = Trainer(network, x_train, t_train, x_val, t_val,epochs=epocs, mini_batch_size=100,optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)trainer.train()return trainer.test_acc_list, trainer.train_acc_list# 超参数的随机搜索======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):# 指定搜索的超参数的范围===============weight_decay = 10 ** np.random.uniform(-8, -4)lr = 10 ** np.random.uniform(-6, -2)# ================================================val_acc_list, train_acc_list = __train(lr, weight_decay)print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)results_val[key] = val_acc_listresults_train[key] = train_acc_list# 绘制图形========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)plt.subplot(row_num, col_num, i+1)plt.title("Best-" + str(i+1))plt.ylim(0.0, 1.0)if i % 5: plt.yticks([])plt.xticks([])x = np.arange(len(val_acc_list))plt.plot(x, val_acc_list)plt.plot(x, results_train[key], "--")i += 1if i >= graph_draw_num:breakplt.show()

运行结果如下：

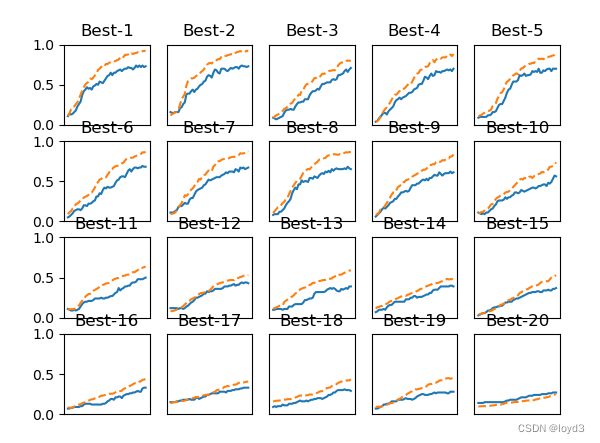
按识别精度从高到低的顺序排列了验证数据的学习的变化从图中可知，直到“Best-5”左右，学习进行得都很顺利。

“Best-5”的超参数的值如下：
Best-5 (val acc:0.73) | lr:0.0052, weight decay:8.97e-06

从这个结果可以看出，学习率在0.001到0.01、权值衰减系数在10的负8次方到10的负4次方之间时，学习可以顺利进行。

本文链接：https://my.lmcjl.com/post/2144.html