| 一、实验目的: 理解并掌握动态规划算法的基本思想和设计步骤。 |
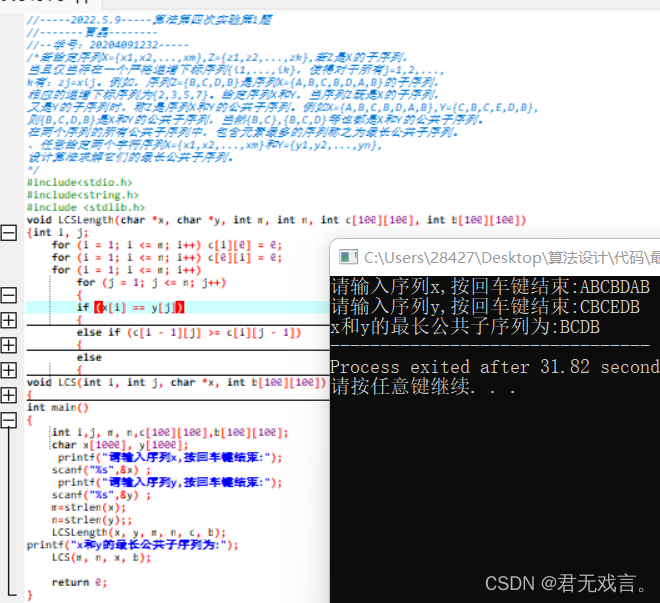
若给定序列X={x1,x2,...,xm},Z={z1,z2,...,zk},若Z是X的子序列,当且仅当存在一个严格递增下标序列{i1,...,ik},使得对于所有j=1,2,...,k有:zj=xij。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。 给定序列X和Y,当序列Z既是X的子序列,又是Y的子序列时,称Z是序列X和Y的公共子序列。例如X={A,B,C,B,D,A,B},Y={C,B,C,E,D,B},则{B,C,D,B}是X和Y的公共子序列,当然{B,C},{B,C,D}等也都是X和Y的公共子序列。在两个序列的所有公共子序列中,包含元素最多的序列称之为最长公共子序列。、任意给定两个字符序列X={x1,x2,...,xm}和Y={y1,y2,...,yn},设计算法求解它们的最长公共子序列。 程序代码: #include<stdio.h> #include<string.h> #include <stdlib.h> void LCSLength(char *x, char *y, int m, int n, int c[100][100], int b[100][100]) { int i, j; for(i=1;i<=m;i++)c[i][0]=0; for(i=1;i<=n;i++)c[0][i]=0; for(i=1;i<=m;i++) for(j=1;j<=n;j++) { if(x[i]==y[j]) { c[i][j]=c[i-1][j-1]+1; b[i][j]=1; } else if (c[i - 1][j] >= c[i][j - 1]) { c[i][j]=c[i-1][j]; b[i][j]=2; } else { c[i][j] = c[i][j - 1]; b[i][j] = 3; } } } void LCS(int i, int j, char *x, int b[100][100]) { if (i == 0 || j == 0) return; if (b[i][j] == 1) { LCS(i-1,j-1,x,b); printf("%c", x[i]); } else if (b[i][j] == 2) LCS(i-1,j,x,b); Else LCS(i,j-1,x,b); } int main() { int i,j, m, n,c[100][100],b[100][100]; char x[1000], y[1000]; printf("请输入序列x,按回车键结束:"); scanf("%s",&x) ; printf("请输入序列y,按回车键结束:"); scanf("%s",&y) ; m=strlen(x); n=strlen(y); LCSLength(x, y, m, n, c, b); printf("x和y的最长公共子序列为:"); LCS(m, n, x, b); return 0; } 程序测试及运行结果:
|
| 分析与讨论:
我的思路是,本题采用动态规划法,最重要的就是找出递推公式,也是本体解开的核心,求出递推公式,再自下而上的求解最优值。设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则:若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。若xm≠yn且zk≠xm,则Z是xm-1和Y的最长公共子序列。若xm≠yn且zk≠yn,则Z是X和yn-1的最长公共子序列。 那么最长公共子序列的长度可以表示为:
在编写程序的时候,当两个序列其中一个为零的时候,那么公共子序列长度肯定为零所以由c[i][0]=0和c[0][j]=0,然后根据最长公共子序列长度,用if与语句分三种情况讨论,并对c[i][j]进行赋值。
求解最长公共子序列的特点:两个序列的最长公共子序列不是唯一的,其子序列不能改变其元素的先后顺序。 动态规划法的优点:能够得到全局最解。 动态规划法缺点:数值方法求解时存在维数灾并且没有统一的标准模型。 |
本文链接:https://my.lmcjl.com/post/2695.html

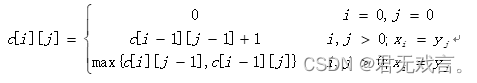
4 评论