本文首发自 HyperAI 超神经微信公众平台~

根据新华社在 2022 年发布的一篇报道，药物研发周期通常长达 10-15 年，资金投入约为 10-20 亿美元，其技术进步和迭代非常缓慢，尤其以制药领域最成熟的剂型之一固体制剂为例，100 多年来并未出现颠覆性技术，其投产上市仍面临着活性药物成分稳定性、释放动力学和生物利用度等关键性障碍。

传统制药方法虽然适用于单一制剂的大规模生产，然而在早期临床试验中，通常会对药物进行剂量递增的研究，以确定最佳及最安全的患者剂量，因此对于较小批量的试验药物，传统制药方法并不适用。

3D 打印因其具备高度灵活性，且生产过程数字化、连续化，在药物设计、制造和使用上，能够一定程度上减缓甚至克服以上障碍。

其中，药物喷墨打印不仅提供了数字化控制打印的能力，还具有控制剂量和自由设计的优势，为个性化给药提供了可能。药物喷墨打印中，墨水特性的优化以及印刷效果一直以来都是研究的焦点，以往研究人员会依据奥内佐格数来预测墨水的可打印性，然而，这种传统预测方法往往会不准确。

近期，来自圣地亚哥德孔波斯特拉大学 (Universidade de Santiago de Compostela) 的 Paola Carou-Senra 以及来自伦敦大学学院 (University College London) 的 Jun Jie Ong 等研究人员开创性地将机器学习模型应用于预测生物墨水可打印性，并成功地提高了预测率。目前该研究已发布在《International Journal of Pharmaceutics: X》期刊上，标题为「Predicting pharmaceutical inkjet printing outcomes using machine learning」。

图 1：该研究成果已发表在《International Journal of Pharmaceutics: X》

论文地址：

https://www.sciencedirect.com/science/article/pii/S2590156723000257

实验概述

奥内佐格数 (Ohnesorge) 是流体力学中用来度量黏性力与惯性力和表面张力的相互关系的无量纲数，主要用于预测墨水的可打印性。可打印配方中，0.1 < Ohnesorge < 1，即 1 < Z < 10 (Z 值是 Ohnesorge 倒数) 时，通常认为墨水可打印。然而很多例外情况下，Z > 10 时墨水也是可打印的。

  图 2：可打印配方 Z 和 Ohnesorge 的直方图和箱线图

如图 1 所示，本研究中可打印墨水配方中的 Z 值处于 1 至 62.2 之间，其中有 68 组墨水配方的 Z 值大于 10。由此可见，单纯依据 Z 值来预测可打印性并不准确。为了提高可打印性预测的准确度，研究人员采用了机器学习模型，并对比了几种不同模型性能。 

实验过程

数据集 

本研究数据集包含从 Google Scholar, PubMed, Web of Science, PubChem, the Handbook of Pharmaceutical Excipients (9th ed.) 上搜集的 2000 年 5 月至 2022 年 2 月期间出版的 75 篇英文文献的研究成果，同时还添加了 2 种内部配方信息。最终，数据集共有 687 种配方。其中，可打印配方 636 种，占总配方的 92.6%，不可打印配方 51 种，占 7.4%。

数据集中包括与喷墨打印过程有关的参数信息，具体变量如下图所示：

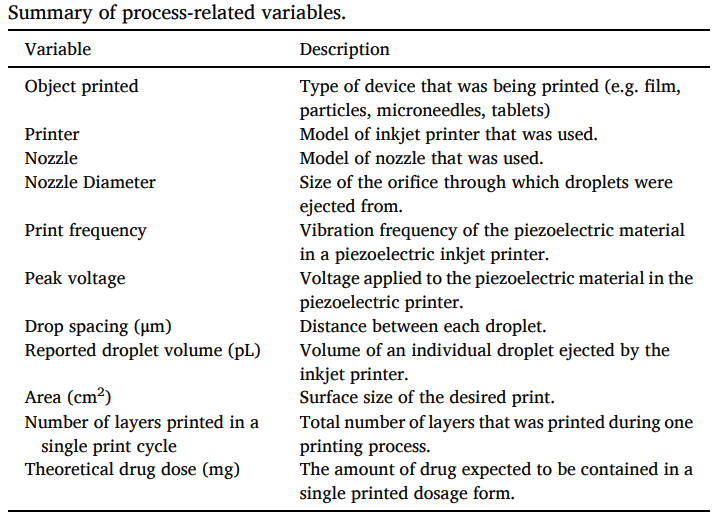
表 1：打印过程中的变量

模型开发 

本项研究中，研究人员开发了三种机器学习模型：人工神经网络 (artificial neural networks, ANN)、  支持向量机 (support vector machines, SVM)、随机森林 (random forests, RF)，并通过计算其科恩卡帕系数 (the Cohen’s kappa coefficient, kappa)、判定系数 (coefficient of determination, R²) 和平均绝对误差 (Mean Absolute Deviation, MAE)，对比得出最佳预测模型。同时，实验过程中，研究人员还探究了模型、特征集以及超参数的组合关系。

* kappa: kappa 是一个用于检验一致性的指标，也可以用于衡量分类的效果，可检测模型预测结果和实际分类是否一致。其取值范围为 -1 到 1 之间，通常大于 0，其中 1 代表完全一致，0 代表随机一致，-1 代表完全不一致。 

* R²:  判定系数，又称可决系数、决定系数，该指标建立在对总离差平方和进行分解的基础之上，用来说明  回归 方程对观测数据拟合程度的一个度量值。判定系数越高，说明对观测数据的拟合程度越好，反之判定系数越小，拟合程度越差。

* MAE:  平均绝对误差，又称平均绝对离差，表示预测值和观测值之间绝对误差的平均值，因而可以准确反映实际预测误差的大小。其取值范围为 [0,+∞)，当预测值与真实值完全吻合时等于 0，即完美模型；该值越大，误差越大。

超参数调优 

可打印墨水虽然可喷射，但也可能会产生卫星液滴，这种形状会导致印刷不准确，是评估墨水质量的重要指标。同时，墨水中药物不足的话，打印的药物无法达到治疗效果，因此墨水中药物的含量也是评估质量的重要指标。因此，本研究中模型除了被用来预测墨水的可打印性，还被用来预测可打印墨水的质量以及墨水中药物剂量。

在预测这两个不同方面的实验中，研发人员对模型超参数进行了优化，其中，初始状态下模型默认超参数如下表：

表 2：模型默认超参数

超参数，是机器学习  算法 中需要手动设置的一些参数。通常情况下，超参数的值对于模型性能和泛化能力有很大的影响。超参数调优（或超参数优化）是通过一定方法，自动寻找最优参数组合的过程。研究人员首先为每个模型预定义了可能取值集合，再通过对训练集进行 5 倍交叉验证的网格搜索来确定最佳超参数值，最后优化后的机器学习模型被应用于测试集。

实验结果 

在预测墨水可打印性方面，最佳预测模型为 RF 模型。研究人员指出经过优化后的 RF 模型准确率为 97.22%，kappa 系数为 0.854，这说明该模型在预测可打印性上准确率高且可靠。

在预测墨水质量，即预测可打印墨水是否产生卫星液滴方面，最佳预测模型为 ANN 模型。研究人员指出经过优化后的 ANN 模型准确率为 97.14% ，kappa 系数为 0.74。这里他们也强调，kappa 系数考虑了偶然得出正确预测的可能性，所以数据集 (数据集中大部分为可打印配方，不可打印配方占比极小) 会相对不均衡，不过即便如此，模型获得的分数和准确率表明预测是可靠的。

制药喷墨打印时，预测药物剂量方面，最佳预测模型为 RF 模型。这里，研究人员指出如果采用预定义超参数及材料名称分组的特征集，RF 模型性能最佳；如果移除残差数据集最小  阈值 ，最佳预测模型为 ANN 模型，下图为训练两个模型不同的数据集。

如图 3 所示，两个数据集的测量药物剂量的分布相似，但用于训练 RF 模型的数据集规模更大，且药物剂量在 2.5-5.0mg 之间的数据比例相对较高（药物喷墨打印中使用的典型药物剂量范围）。因此，尽管 ANN 模型的表现略好于 RF 模型，但 RF 模型更适合于优化。优化模型后的 RF 模型的 R² 为 0.800，MAE 为 0.291，表明其可以预测药物剂量，误差在 ±0.291 mg 范围内。

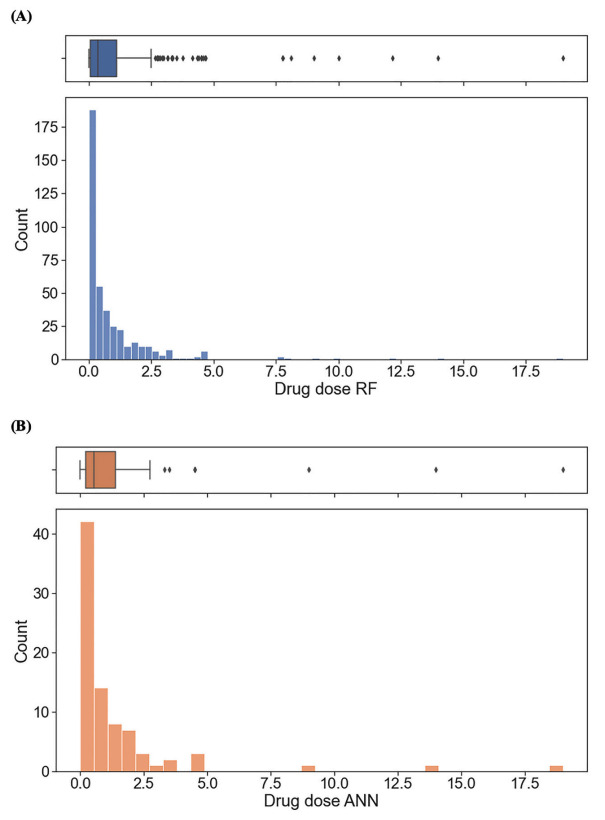
图 3：训练 RF 和 ANN 模型数据集中测量药物剂量图

综上，机器学习模型能够预测可打印墨水的可打印性、打印质量，同时还能够预测药物剂量，其中，不同算法和特征集还能对预测结果产生不同影响。

药物 3D 打印：推动产业走向数字化

3D 打印在药物研发的早期阶段，提供了更大的灵活性，只需调整几个参数，就可以更容易地改变药物的形状、大小、剂量、释放情况等，加快临床试验的进度、缩短新药上市的周期。同时，还能通过为患者量身定制精确剂量，提供个性化医学治疗。

2015 年 7 月，美国制药公司 Aprecia 利用 3D 打印技术制备的处方药 SPRITAM（左乙拉西坦）速溶片上市，用于治疗癫痫。这是全球首个获得美国食品药品监督管理局 (FDA) 批准的 3D 打印药物，标志着药物 3D 打印已成为现实，同时也掀起了一轮 3D 打印药物的研究热潮。此后，Aprecia 根据自身优势，成功转型为一家药物制剂技术平台公司，并与普渡大学药剂学院等科研机构以及大型跨国药企积极开展合作、促进新药研发。

放眼国内，成立于 2015 年的南京三迭纪医药，则堪称国内 3D 打印药物领域的引领者。三迭纪医药由成森平博士和美国制剂界专家和教育家李霄凌 (Xiaoling Li) 教授共同创立，成立至今，其首创了 MED 技术，成功开发了从药物剂型设计、数字化产品开发，到智能制药全链条的专有 3D 打印技术平台，其研发的 3 款 3D 打印药物–T19（针对类风湿性关节炎）、T20（降低非瓣膜病性房颤患者的卒中和全身性栓塞风险等）、T21（治疗溃疡性结肠炎），均已获得美国 FDA 临床试验批准，进入临床阶段。

无疑，药物 3D 打印构建了数字化制药的基础，其市场远期需求量大、前景可期。根据 Grandview Research 发布的一份报告，全球药物 3D 打印市场或将在不久的未来呈现指数级增长，预计到 2030 年，全球药物 3D 打印市场将达到 2.6974 亿美元，而老龄化的加剧，无疑创造了巨大的个性化医疗窗口。相信在不久的将来，药物 3D 打印将重塑生物制药的商业格局。

参考链接：

[1]http://www.news.cn/mrdx/2022-09/13/c_1310662292.htm

[2]https://www.pudong.gov.cn/019010005/20221026/741820.html

本文首发自 HyperAI 超神经微信公众平台~

本文链接：https://my.lmcjl.com/post/3519.html