导航

• LSTM原理
• GRU原理
• Seq2Seq架构
• • 编码信息损失
• 参考资料

LSTM原理

一般RNN中仅有一个隐藏状态单元hth_tht​，且不同时刻的隐藏状态单元的参数是共享的，这种结构导致了RNN存在长期依赖问题，只能对短期输入敏感.
LSTM在普通RNN上加入了元胞状态单元ctc_tct​，在不同的时刻有着可变的连接权重，ctc_tct​通过对hth_tht​的调节形成长短期记忆.

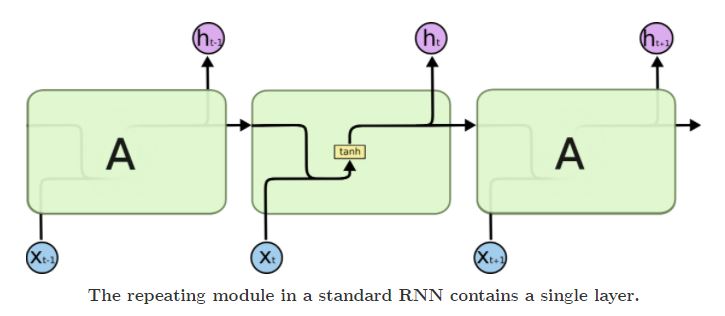
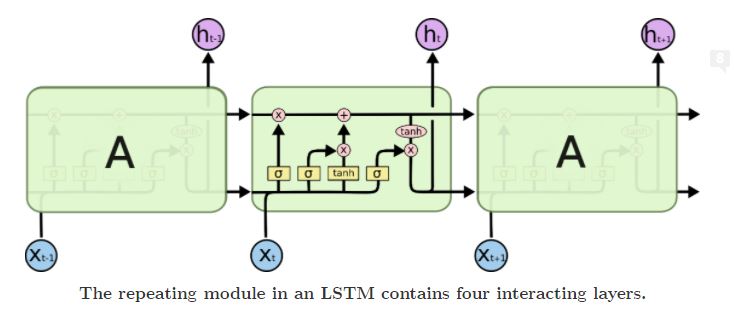
LSTM引入了门控单元，对于每个时刻ttt，LSTM有输入门iti_tit​，遗忘门ftf_tft​和输出门oto_tot​等3个门控单元，每个门控单元的输入包括当前时刻的序列信息xtx_txt​和上一时刻的隐藏状态单元ht−1h_{t-1}ht−1​，计算方程为
{it=σ(Wixt+Uiht−1+bi)ft=σ(Wfxt+Ufht−1+bf)ot=σ(W0xt+Uoht−1+b0)\left\{ \begin{aligned} &i_t=\sigma(W_ix_t+U_ih_{t-1}+b_i)\\ &f_t=\sigma(W_fx_t+U_fh_{t-1}+b_f)\\ &o_t=\sigma(W_0x_t+U_oh_{t-1}+b_0) \end{aligned} \right. ⎩⎪⎨⎪⎧​​it​=σ(Wi​xt​+Ui​ht−1​+bi​)ft​=σ(Wf​xt​+Uf​ht−1​+bf​)ot​=σ(W0​xt​+Uo​ht−1​+b0​)​
3个门控单元的计算方式均为全连接层，区别仅在于权重矩阵和偏置，激活函数σ(⋅)\sigma(\cdot)σ(⋅)一般使用sigmoid函数，取值范围为[0,1][0, 1][0,1]，将门控单元与信号数据做逐元素相乘，可以控制信号通过门控后要保留的信息量，可以设置当门控单元状态为0时，信号被全部丢弃；当状态为1时，信号被全部保留；而当状态在[0,1][0, 1][0,1]时，部分信号被保留.

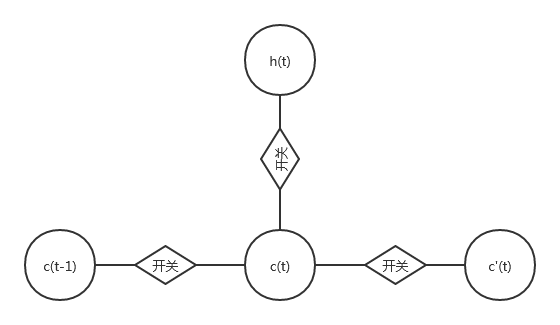
从示意图中可以看出，元胞状态单元从上一时刻的ct−1c_{t-1}ct−1​到当前时刻的ctc_tct​转移是由输入门和遗忘门共同控制的，输入门决定了当前时刻输入信息c~(t)\tilde{c}(t)c~(t)有多少被吸收，遗忘门决定了上一时刻元胞状态单元ct−1c_{t-1}ct−1​有多少未被遗忘，最终的元胞状态单元ctc_tct​由两个门控处理后的信号综合产生.
c~t=tanh⁡(Wcxt+Ucht−1+bc)ct=ft⊙ct−1+it⊙c~t\begin{aligned} &\tilde{c}_t=\tanh(W_cx_t+U_ch_{t-1}+b_c)\\ &c_t=f_t\odot c_{t-1}+i_t\odot\tilde{c}_t \end{aligned} ​c~t​=tanh(Wc​xt​+Uc​ht−1​+bc​)ct​=ft​⊙ct−1​+it​⊙c~t​​
其中，⊙\odot⊙表示逐元素点乘操作，LSTM的隐藏状态单元hth_tht​则由输出门和ctc_tct​共同决定
ht=ot⊙tanh⁡(ct)h_t=o_t\odot\tanh(c_t) ht​=ot​⊙tanh(ct​)
可以看出，在LSTM中，不仅隐藏单元ht−1h_{t-1}ht−1​和hth_tht​之间存在连接，ct−1c_{t-1}ct−1​和ctc_tct​之间也存在线性自循环的关系，这种线性自循环是一种滑动处理信息的机制，当门控单元开启时，记住过去的信息；当门控单元关闭时，丢弃过去的信息，这种线性自循环的机制使得LSTM可以解决RNN中长期依赖的问题.

GRU原理

考虑设计一种仅有两个门控单元的RNN，其中一个门控单元控制短期记忆，另一个门控单元控制长期记忆，Kyunghyun Cho等提出的GRU模型使用更少的参数实现了LSTM的功能.

LSTM有两个状态单元hth_tht​和ctc_tct​，GRU使用了一个状态单元hth_tht​，两个门控单元，重置门rtr_trt​和更新门ztz_tzt​，每个门控单元的输入包括当前时刻的序列信息xtx_txt​和上一时刻的隐藏状态单元ht−1h_{t-1}ht−1​，计算方程为
rt=σ(Wrxt+Urht−1)zt=σ(Wzxt+Uzht−1)\begin{aligned} &r_t=\sigma(W_rx_t+U_rh_{t-1})\\ &z_t=\sigma(W_zx_t+U_zh_{t-1}) \end{aligned} ​rt​=σ(Wr​xt​+Ur​ht−1​)zt​=σ(Wz​xt​+Uz​ht−1​)​
在GRU中，重置门决定之前的隐藏状态单元是否被忽略，更新门则控制当前隐藏状态单元是否被新的隐藏状态更新.
h~t=tanh⁡(Whxt+Uh(rt⊙ht−1))ht=(1−zt)ht−1⏟上一时刻保留信息+zth~t⏟当前时刻记忆下的信息\begin{aligned} &\tilde{h}_t=\tanh(W_hx_t+U_h(r_t\odot h_{t-1}))\\ &h_t=\underbrace{(1-z_t)h_{t-1}}_{\text{上一时刻保留信息}}+\underbrace{z_t\tilde{h}_t}_{\text{当前时刻记忆下的信息}} \end{aligned} ​h~t​=tanh(Wh​xt​+Uh​(rt​⊙ht−1​))ht​=上一时刻保留信息(1−zt​)ht−1​​​+当前时刻记忆下的信息zt​h~t​​​​
可以发现，遗忘和记忆的权重设定为互补关系.

Seq2Seq架构

在Seq2Seq中，由于输入序列与输出序列不是等长的，所以对整个序列的处理分为理解（编码）和翻译（解码）两个步骤，并且编码器和解码器可以在两个不同的RNN上并行实现.

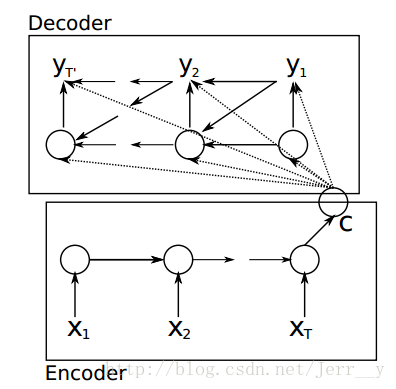
Seq2Seq采用一个固定尺寸的状态向量CCC作为编码器与解码器之间的桥梁，编码器可以是一个简单的RNN，输入序列为X=(x1,x2,…,xT)X=(x_1, x_2, \dots, x_T)X=(x1​,x2​,…,xT​)，其隐藏状态hth_tht​的计算公式为
ht=f(ht−1,xt)h_t=f(h_{t-1}, x_t) ht​=f(ht−1​,xt​)
其中f(⋅)f(\cdot)f(⋅)是非线性激活函数，将最后时刻的隐藏状态hTh_ThT​作为状态向量输入到解码器.
解码器根据状态向量CCC生成长度可变的解码序列Y=(y1,y2,…,yT′)Y=(y_1, y_2, \dots, y_{T'})Y=(y1​,y2​,…,yT′​)，解码器同样可以使用一个简单的RNN实现，其隐藏状态hth_tht​计算公式为
ht=f(ht−1,yt−1,C)h_t=f(h_{t-1}, y_{t-1},C) ht​=f(ht−1​,yt−1​,C)
其中，yt−1y_{t-1}yt−1​是上一时刻的输出，f(⋅)f(\cdot)f(⋅)是非线性激活函数，解码器的输出由如下公式确定
P(yt∣yt−1,yt−2,…,yt,C)=g(ht,yt−1,C)P(y_t\mid y_{t-1}, y_{t-2}, \dots, y_t, C)=g(h_t, y_{t-1}, C) P(yt​∣yt−1​,yt−2​,…,yt​,C)=g(ht​,yt−1​,C)
其中g(⋅)g(\cdot)g(⋅)会产生一个概率分布，解码器工作流程如图所示

或者使用一种更加简单的方式实现解码器，仅在初始时刻需要状态向量CCC，其他时刻仅接受隐藏状态和上一时刻的输出信息
P(yt)=g(ht,yt−1)P(y_t)=g(h_t, y_{t-1}) P(yt​)=g(ht​,yt−1​)

在训练阶段，需要让模型输出的解码序列尽可能正确，可以通过MLE方法配合贪心算法实现
max⁡θ1N∑n=1Nlog⁡pθ(Yn∣Xn)\max_\theta\frac{1}{N}\sum_{n=1}^N\log p_\theta(Y_n\mid X_n) θmax​N1​n=1∑N​logpθ​(Yn​∣Xn​)
解码器每次根据当前状态和已解码序列，选择出最佳解码结果，直到算法收到终止信号.

编码信息损失

由于Seq2Seq中只用固定大小的状态向量连接编码模块和解码模块，这就要求编码器将整个输入序列的信息压缩到状态向量中，这个过程存在编码损失，一般的解决方案有序列翻转法.
Bahdanau（2014）提出了注意力机制模型，将状态向量CCC设置为动态，即
P(yt)=g(ct,yt,…,yt−1)P(y_t)=g(c_t, y_t, \dots, y_{t-1}) P(yt​)=g(ct​,yt​,…,yt−1​)
其中，ctc_tct​是专门针对ttt时刻的状态向量.

参考资料

Understanding LSTM Networks
百面深度学习 中国工信出版集团 葫芦娃
LSTM和GRU讲解
Seq2Seq学习笔记

本文链接：https://my.lmcjl.com/post/6282.html