一、实验内容

1.利用改进的jakes模型来产生单径的平坦型瑞利衰落信道。

（1）创建rayleigh.m文件。

1）计算振荡器数目；

2）计算信道函数的实部；

3）计算信道函数的虚部；

4）乘归一化功率系数得到传输函数；

5）计算冲激响应函数；

（2）创建rayleigh1.m文件。

调用rayleigh.m文件计算多普勒频移分别为10Hz，20Hz，30Hz和60Hz时的信道功率。

2. 利用QPSK信号通过瑞利衰落信道后的误比特率和误符号率，并与AWGN信道下的误比特率和误符号率进行对比。

二、实验结果

1.改进的jakes模型产生瑞利衰落信道

实验一：利用改进的jakes模型来产生单径的平坦型瑞利衰落信道。

（1）实验代码

代码1：rayleigh.m文件

%利用改进的jakes模型来产生单劲的平坦型瑞利衰落信道
%通过rayleigh1.m文件来调用function [h]=rayleigh(fd,t)%fd;信道的最大多普勒频移，单位Hz。%t:信号的抽样时间序列。%h:h为输出的瑞利信道函数，是一个时间函数复序列。
N=40;   %假设的入射波数目。
wm=2*pi*fd;     %每象限的入射波数目，即振荡器数目。
N0=N/4;     %信道函数的实部。
Tc=zeros(1,length(t));  %信道函数的虚部。
Ts=zeros(1,length(t));  %归一化功率系数。
P_nor=sqrt(1/N0);   %区别各条路径的均匀分布随机相位。
theta=2*pi*rand(1,1)-pi;
for ii=1:N0alfa(ii)=(2*pi*ii-pi+theta)/N;  %第i条入射波的入射角。%对每个载波而言在（-pi，pi）之间均匀分布的随机相位fi_tc=2*pi*rand(1,1)-pi;fi_ts=2*pi*rand(1,1)-pi;%计算冲激响应函数Tc=Tc+cos(cos(alfa(ii))*wm*t+fi_tc);Ts=Ts+cos(sin(alfa(ii))*wm*t+fi_ts);
end
h=P_nor*(Tc+j*Ts);  %乘归一化功率系数得到传输函数。

代码2：rayleighchan1文件

%产生最大多普勒频移
%调用rayleigh.m文件ts=1/1000;  %信号抽样时间间隔。
t=0:ts:1;   %生成时间序列。fd=10;  %多普勒频移为10。
h1=rayleigh(fd,t);  %产生信道数据。
subplot(2,2,1);plot(20*log10(abs(h1(1:1000))),'b');
title('fd=10Hz时的信道功率曲线');
xlabel('时间','fontname','黑体','fontsize',10);ylabel('功率','fontname','黑体','fontsize',10);
grid on;fd=20;  %多普勒频移为20。
h2=rayleigh(fd,t);  %产生信道数据。
subplot(2,2,2);plot(20*log10(abs(h2(1:1000))),'r');
title('fd=20Hz时的信道功率曲线');
xlabel('时间','fontname','黑体','fontsize',10);ylabel('功率','fontname','黑体','fontsize',10);
grid on;fd=30;  %多普勒频移为30。
h3=rayleigh(fd,t);  %产生信道数据。
subplot(2,2,3);plot(20*log10(abs(h3(1:1000))),'m');
title('fd=30Hz时的信道功率曲线');
xlabel('时间','fontname','黑体','fontsize',10);ylabel('功率','fontname','黑体','fontsize',10);
grid on;fd=60;  %多普勒频移为60。
h4=rayleigh(fd,t);  %产生信道数据。
subplot(2,2,4);plot(20*log10(abs(h4(1:1000))),'g');
title('fd=60Hz时的信道功率曲线');
xlabel('时间','fontname','黑体','fontsize',10);ylabel('功率','fontname','黑体','fontsize',10);
grid on;

（2）实验结果

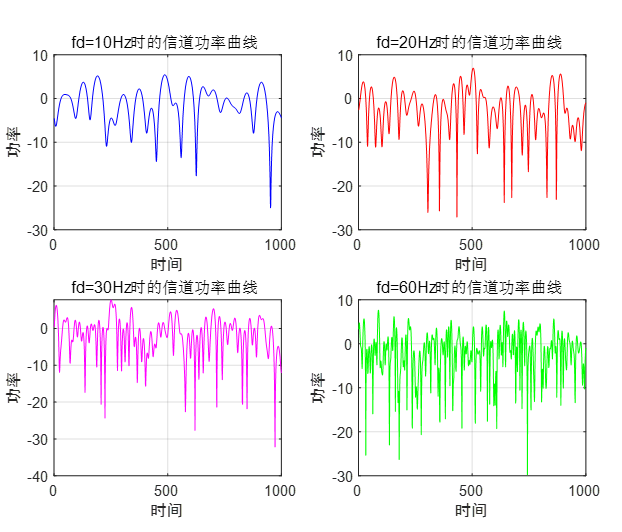
 2.瑞利衰落信道传输

实验二：利用QPSK信号通过瑞利衰落信道后的误比特率和误符号率，并与AWGN信道下的误比特率和误符号率进行对比。其中，多普勒频移为100Hz，经过矩形脉冲成形后的信号抽样时间间隔为1/800000s。

（1）实验代码

%QPSK在AWGN和Rayleigh下的性能
nSamp=8;    %矩形脉冲的取样点。
numSymb=10000;  %每种SNR下的传输符号数。
ts=1/(numSymb*nSamp);
t=(0:numSymb*nSamp-1)*ts;
M=4;    %QPSK的符号类型书。
SNR=-3:3;   %SNR的范围。
grayencod=[0,1,3,2];    %Gray的 编码格式。for ii=1:length(SNR);msg=randsrc(1,numSymb,[0:3]);   %产生发送信号。msg_gr=grayencod(msg+1);    %进行Gray编码影射。msg_tx=pskmod(msg_gr,M);    %QPSK调制。msg_tx=rectpulse(msg_tx,nSamp);     %产生矩形成形。h=rayleigh(10,t);   %生成瑞利衰落。msg_tx1=h.*msg_tx;  %信号通过瑞利衰落信道。msg_rx=awgn(msg_tx,SNR(ii));    %通过AWGN信道。msg_rx1=awgn(msg_tx1,SNR(ii));msg_rx_down=intdump(msg_rx,nSamp);  %匹配滤波相干解调。msg_rx_down1=intdump(msg_rx1,nSamp);msg_gr_demod=pskdemod(msg_rx_down,M);   %QPSK解调。msg_gr_demod1=pskdemod(msg_rx_down1,M);[dummy graydecod]=sort(grayencod);graydecod=graydecod-1;msg_demod=graydecod(msg_gr_demod+1);    %Gray编码逆映射。msg_demod1=graydecod(msg_gr_demod1+1);[errorBit BER(ii)]=biterr(msg,msg_demod,log2(M));   %计算BER。[errorBit1 BER1(ii)]=biterr(msg,msg_demod1,log2(M));    %计算BER1。[errorSym SER(ii)]=symerr(msg,msg_demod);     %计算SER。[errorSym SER1(ii)]=symerr(msg,msg_demod1);     %计算SER1。
endfigure;
semilogy(SNR,BER,'-bx',SNR,SER,'-ro',SNR,BER1,'-k.',SNR,SER1,'-m*','markersize',7);     %画出BER和SNR随SNR变化的曲线。
legend('AWGN信道BER','AWGN信道SER','Rayleigh衰落+AWGN信道BER','Rayleigh衰落+AWGN信道SER','fontname','黑体','location','b');
title('QPSKzai Rayleigh衰落信道下的性能','fontname','黑体','fontsize',10);
xlabel('信噪比(dN)','fontname','黑体','fontsize',10);
ylabel('误符号率和误比特率','fontname','黑体','fontsize',10);

2实验结果

本文链接：https://my.lmcjl.com/post/7783.html