Python有不少求根的办法，但是都是求一重根的，不太适用。 在这个问题上用的是暴力搜索法：记 $$F(x)=f(x)-y$$ 判断每个 x 对应的 $F(x)$ 的符号，如果$F(x_i)<0,\ F(x_{i+1})>0$，或者$F(x_i)>0,\ F(x_{i+1})<0$，则取该$F(x)=0$的根为$$x_0=(x_i+x_{ 继续阅读

数理介绍，不喜欢数学的言下之意也就是绝大部分人可以略过了。 简单推导 假设f(x)是关于X的函数: 求出f(x)的一阶导，即斜率: 简化等式得到: 然后利用得到的最终式进行迭代运算直至求到一个比较精确的满意值，为什么可以用迭代法呢?理由是中值定理(Intermediate Value Theorem): 如果f函数在闭区间[a,b]内连续，必存在一点x使得f(x) = c，c是函数f在闭区间[a,b]内的一点 继续阅读

本文主要介绍Python中交集和并集的用法和示例。Python作为一门强大的编程语言，支持多种数据结构，其中集合是比较常用的一种。而集合的交集和并集是集合运算中重要的概念。在Python中，我们可以使用内置函数set()来创建集合，并使用&操作符获取交集，使用|操作符获取并集。 一、交集 1、交集定义 交集是指两个或多个集合中共有的元素的新集合。在Python中使用&操作符来求两个集合的交集，即a & b。 2、交集示例代码 a = 继续阅读

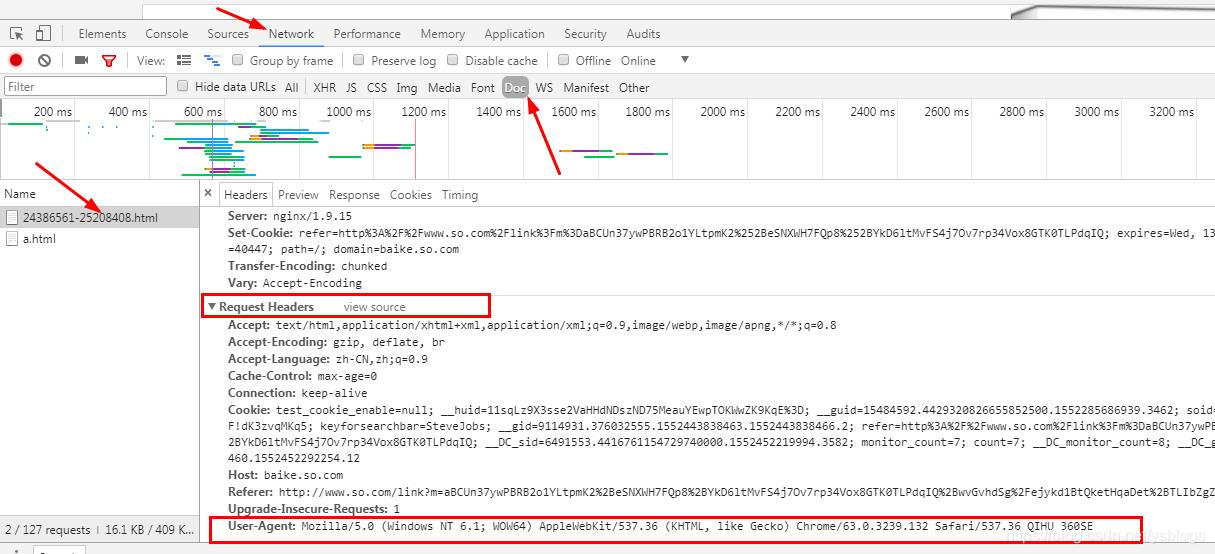
1、为什么要设置headers? 在请求网页爬取的时候，输出的text信息中会出现抱歉，无法访问等字眼，这就是禁止爬取，需要通过反爬机制去解决这个问题。 headers是解决requests请求反爬的方法之一，相当于我们进去这个网页的服务器本身，假装自己本身在爬取数据。 对反爬虫网页，可以设置一些headers信息，模拟成浏览器取访问网站 。 2、 headers在哪里找？ 谷歌或者火狐浏览器，在网页面上点击：右键–&gt 继续阅读

Python是一门流行的编程语言，可以用于各种各样的编程任务。本文将介绍如何在Python中使用根号，从多个方面探讨该主题。 一、math.sqrt（）函数 Python的math库提供了一个sqrt（）函数，可以用于计算任何数字的平方根。下面是使用sqrt（）函数计算平方根的示例代码： import math # 计算数值的平方根 num = 16 sqrt = math.sqrt(num) # 打印结果 print("The square root 继续阅读

本文将从多方面详细阐述Python数字列表逐一提取数字的方法，包括使用循环、递归、lambda函数等方式。读者可以根据具体需求选择合适的方法。 一、循环提取数字 使用循环是最直接、最简单的提取数字的方法，可以通过遍历列表逐一取出数字。下面是一个示例代码： numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] for number in numbers: print(number) 输出结果为： 1 2 3 4 5 6 继续阅读

本文主要介绍如何利用函数图象求解方程，下面从多个方面进行详细阐述。 一、基本概念 在解方程时，我们通常会用到函数图象。函数图象是将一个函数的自变量与因变量之间的关系用图像表示出来，因而也叫做函数的图形或者曲线。 函数图象的表示方法是将自变量和函数值分别作为坐标轴上的横纵坐标，然后用线条或者曲线将坐标点连接起来，形成一个图形。 二、使用函数图象求解一元一次方程 对于形如 $ax+b=0$ 的一元一次方程，我们可以将其变形成 $y=ax+b$ 的函数形式，然后将该 继续阅读

引言 众所周知的是，在大学课程中一般只会教授一种拟合方法(也即参数估计方法)——最小二乘法。这是一种直接求解的方法，非常的有效，不仅是损失最小解，而且是最大似然解。只不过，有一个缺点，它只能解决线性方程参数问题，对于非线性曲线，就无能为力了。大部分情况下还是将其转换成线性问题，再使用最小二乘法。 然而，并非所有的问题都能转换为线性问题，甚至 继续阅读

Python是一门广泛应用于科学计算、数据分析、人工智能等领域的编程语言。其中，循环语句是基础而重要的语法之一，在Python中，while循环可以很方便地实现对某个条件的反复执行，同时也可以用来求1到100的和。 一、while循环语句的基本语法 while 循环的语法格式如下： while 条件： 代码块 其中，条件是一个布尔表达式，如果它的值为True，则执行代码块。执行完代码块后，再次判断条件是否为True，如果是，则继续执行代码块，直到条 继续阅读

本文将从如下几个方面对Python求n的阶乘代码进行详细的阐述： 1. 什么是阶乘，为什么要求阶乘 2. Python求n的阶乘的几种方法 3. Python求阶乘的性能比较 一、什么是阶乘，为什么要求阶乘 阶乘是指从1乘到n的连续整数乘积，常用符号是"!"，例如： n! = 1 * 2 * 3 * ... * (n-1) * n 求阶乘在计算机科学中有很多实际的应用，例如组合数学、排列组合等。同时，在编程中也经常需要求阶乘，例如计算斐波那契数列、概率分布 继续阅读

本文实例讲述了Python基于Floyd算法求解最短路径距离问题。分享给大家供大家参考，具体如下： Floyd算法和Dijkstra算法，相信大家都不陌生，在最短路径距离的求解中应该算得上是最为基础和经典的两个算法了，今天就用一点时间来重新实现一下，因为本科的时候学习数据结构才开始接触的这个算法，当时唯一会用的就是C语言了，现在的话，C语言几乎已经离我远去了，个人感觉入手机器学习以来python更得我心，因为太通俗易懂了，带给你的体验自然也是非常不错的。 当然网 继续阅读

今天正好有点时间就想着把之前零星时间里面做的一点小东西整合一下梳理出来，本文的核心目的就是想要基于python来开发实现各种有趣的数学曲线的可视化展示。 笛卡尔心形线 笛卡尔心形线是一种二维平面曲线，由法国数学家笛卡尔在17世纪提出。它得名于其形状类似于传统的心形符号 ❤️。 笛卡尔心形线的方程可以表示为： (x^2 + y^2 - 1)^3 - x^2 * y^3 = 0 其中，(x, y) 是心形线上的点坐标。 继续阅读