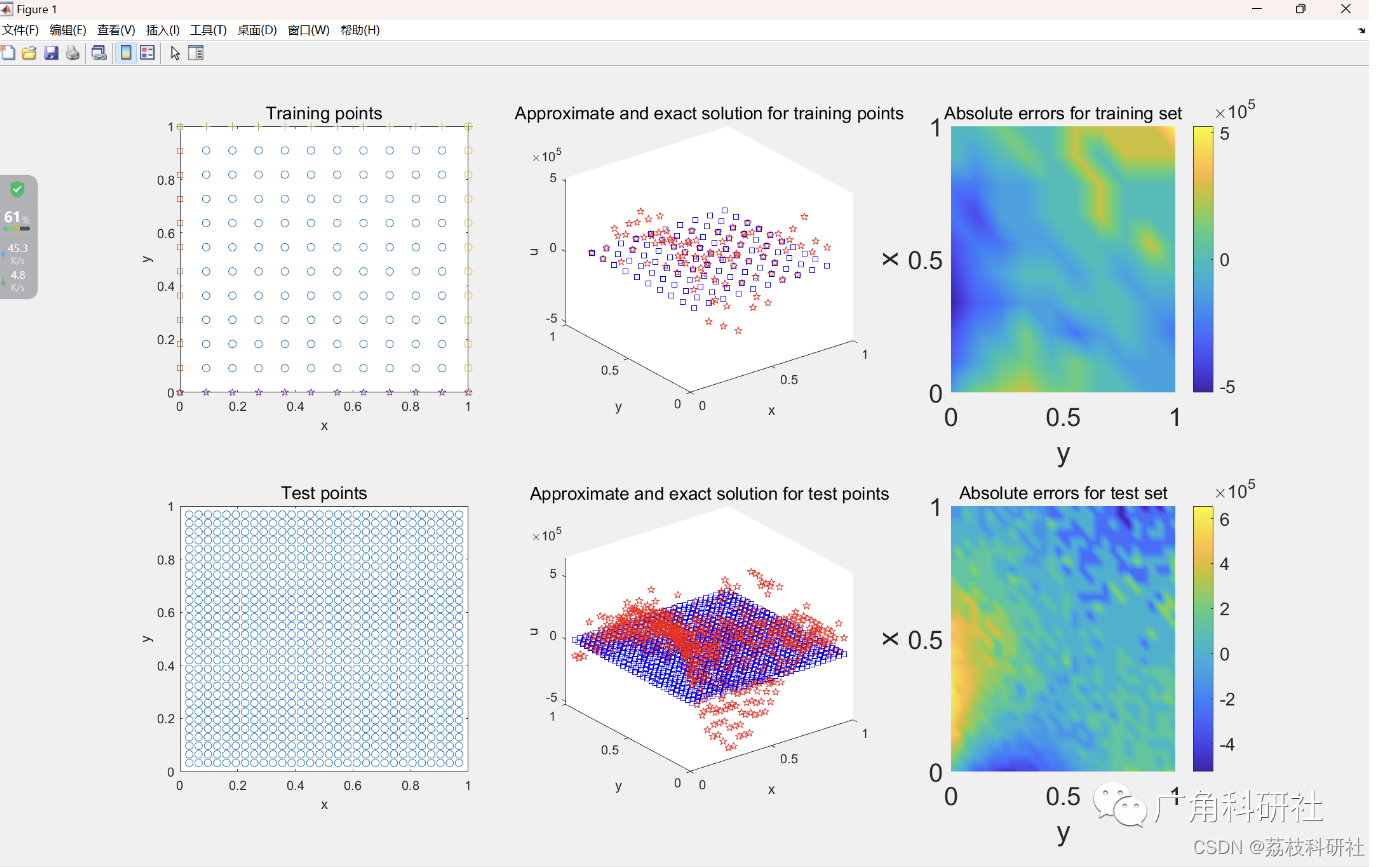
💥1 概述 本代码说明了“最小二乘支持向量机”在学习偏微分方程 （PDE） 解方面的应用。提供了一个示例，并将获得的结果与精确的解决方案进行比较。 📚2 运行结果 部分代码： clc; clear all; close all warning('off','all') a0=0; b0=1; n=11; h=( 继续阅读

文章目录 1 SVM概述1.1 概念1.2 SVM的优缺点1.2.1 优点1.2.2 缺点 2 在python中使用SVM2.1 scikit-learn库2.2 SVM在scikit-learn库中的使用2.2.1 安装依赖库2.2.2 svm.SVC2.2.3 应用实例 总结 1 SVM概述 1.1 概念 支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面&# 继续阅读

标题有点长，但是基本也说明出了这篇文章的主旨，那就是利用GPT AI智能回答自己设置好的问题 既能实现自己的AI知识库机器人，又能节省ChatGPT调用的token成本费用。 代码仓库地址 document.ai: 基于GPT3.5的通用本地知识库解决方案 下面图片是整个流程： 导入知识库数据 利用openai的向量接口生成向量数据，然后导入到向量数据库qdrant 这段代码会将指定目录下的所有文件读取出来， 继续阅读

Zilliz 又双叒叕有好消息传来！ 自 NVIDIA GTC Keynote 被黄老板点名后，Zilliz 又加入“大网红 OpenAI ”的朋友圈——作为首批受邀合作伙伴，向 ChatGPT 贡献了向量数据库插件，打通了知识召回与大型语言模型之间的桥梁！ ChatGPT 联网，向量数据库已加入“团战” 今晨，Open AI 再次向科技行业扔出重磅武器 ——部分解除 ChatGPT 无法联网的 继续阅读

ChatGPT 拓展资料：AI大模型之美 -计算两个向量之间的余弦相似度 本文讲解使用openai.embeddings_utils中的cosine_similarity和get_embedding函数。 首先，让我们了解一下这两个函数的作用： cosine_similarity: 计算两个向量之间的余弦相似度。get_embedding: 获取一个单词或短语的嵌入向量表示。 接下来，我将为你演示如何使用这两个函数： 获取单词或短语的嵌入向量表示：要获取单词或短语的嵌入向量表示，你需要 继续阅读

在Java中，多维数组通常使用嵌套的for循环来遍历元素。在一个二维数组中，第一层循环用于遍历行，第二层循环用于遍历列。在更高维度的数组中，第三、四、五层以及更多层循环分别用于遍历数组的每一维度。 具体来说，第一层循环控制数组的行数，每次循环取出一个行向量；第二层循环控制数组的列数，每次循环取出行向量中的一个元素。通过双层循环的嵌套，可以依次遍历所有的元素&#xff0c 继续阅读

一、几何体的_UV_以及法向属性 UV属性是一组二维坐标，每个顶点都有一个对应的UV坐标。在三维模型上贴上二维的纹理贴图时，需要将所有顶点映射到纹理上的对应位置。UV属性的取值范围一般是[0,1]，表示纹理上的相对位置。通过修改UV属性，可以在UV贴图上切换不同的图案或调整纹理贴图的映射效果。 法向属性是每个顶点的法向量，用于确定顶点所在面的方向和光照效果。在three.js中，光照效果是基于每个顶点的法向 继续阅读

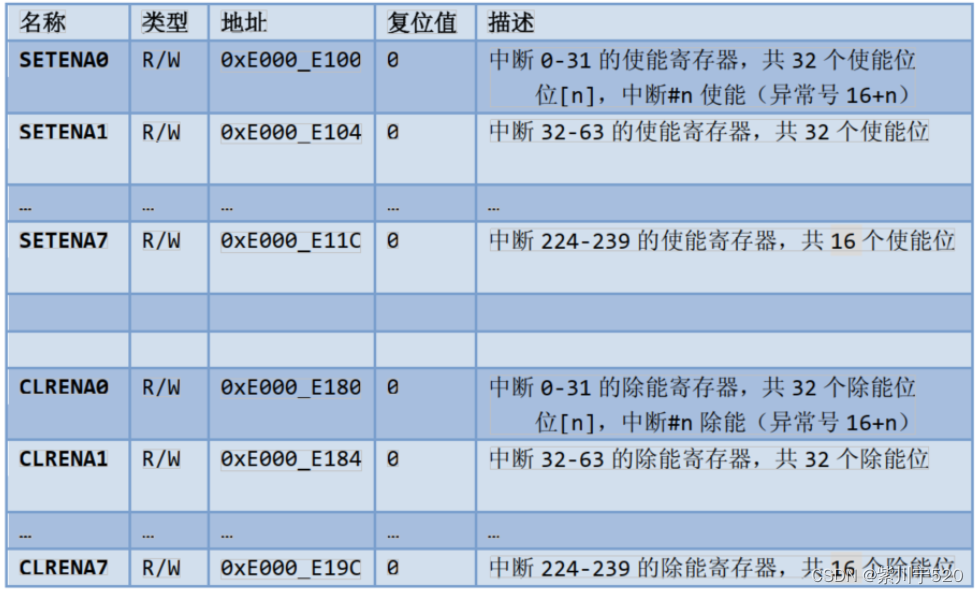
1、NVIC概述         向量中断控制器，简称NVIC，是Cortex-M3不可分离的一部分，它与CM3内核的逻辑紧密耦合。NVIC的寄存器以存储器映射的方式来访问，除了包含控制寄存器和中断处理的控制逻辑之外，NVIC还包含了MPU、SysTick定时器以及调试控制相关的寄存器。         NVIC共支持1至240个外部中断输入（通常外部中断写作IRQs）。具体的数值由芯片厂商在设 继续阅读

先来看几道面试题： 有木有被上面的大大大数据吓到了无从下手啊？今天介绍的BitSet就可以解决这一问题。 简介 一个按需增长的位向量，C++和java都有提供实现。 BitSet是位操作的对象，值只有1和0。用1位来表示一个数据是否出现过，0为没有出现过，1表示出现过。使用用的时候既可根据某一个是否为0表示此数是否出现过。 比较 一般，int占4个字节， 继续阅读

ChatGPT基础知识系列之Embeddings模型 OpenAI的Embeddings(文本嵌入)测量的是文本字符串的相关性。嵌入通常用于： 搜索（根据与查询字符串的相关性对结果进行排名）聚类（其中文本字符串按相似性分组）建议（推荐具有相关文本字符串的项目）异常检测（识别出相关性很小的异常值）多样性测量（分析相似性分布）分类（其中文本字符串按其最相似的标签进行分类） 一个Embedding本质上是一个向量——多个浮点数组成的列表，也就是通过向量来表示文本，两个向量之间的距离测量它们的相 继续阅读

我是小白，请多指教 我是小白，请多指教 我是小白，请多指教 intersect 函数 用去求取两个矩阵或者向量之间的交集。 具体形式 C = intersect(A, B)；C = intersect(A, B, ‘rows’)；[C, ia, ib] = intersect(A, B) 例子 C = intersect(A, B)； 两个矩阵或者向量之间&#xff0 继续阅读

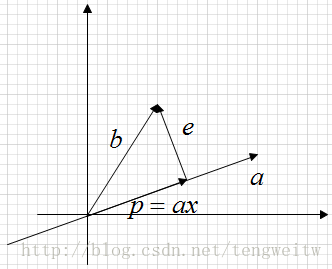
我们在初中就应该学过投影，那么什么是投影呢？形象点说，就是将你需要投影的东西上的每一点向你要投影的平面作垂线，垂线与平面的交点的集合就是你的投影。注意这里我们的投影是向量的投影，几何的投影(并不一定是垂直投影的)可见度娘百科。同样的，我们从简单的二维投影来开始讨论。    1、二维投影 上图表示的是，向量b在向量a上的投影。显然有如下表达式： 其中，P 继续阅读