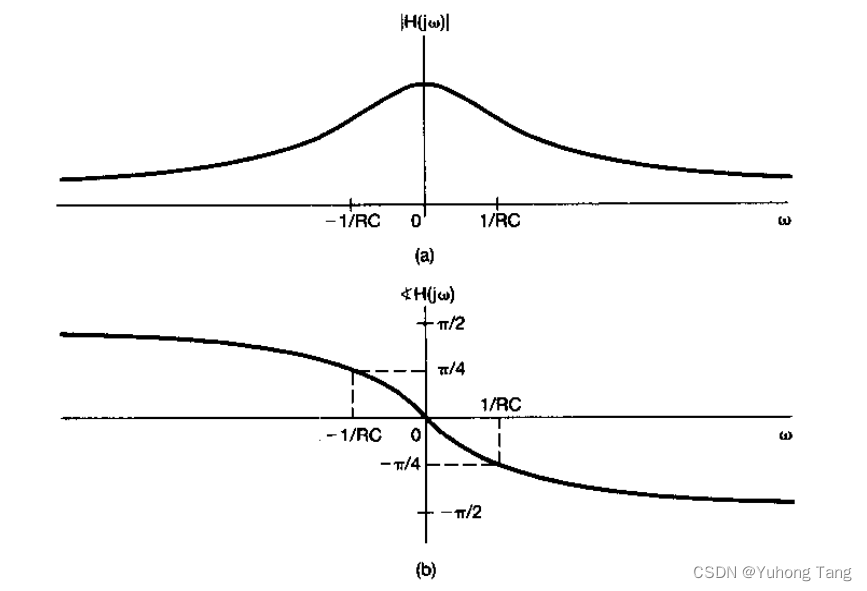
用微分方程描述的连续时间滤波器举例   在许多应用中，频率选择性滤波器是用线性常系数微分或差分方程描述的线性时不变系统来实现的。这有许多理由，例如很多具有滤波作用的物理系统都是由微分或差分方程表征的。这方面的一个很好的例子就是在后续将研究的汽车减震系统，在某种程度上这个系统的设计就是为了滤掉由道路表面不平坦引起的高频颠簸和起伏。利用由微分或差分方程描述的滤波器的第二个原因是，它们能很方便地用模拟硬件或数字硬件来实现。另外，由 继续阅读

模拟滤波器设计的关键是找到一个稳定易实现的逼近函数,且其幅频特性要满足所需滤波器的要求。常用的滤波器模型有巴特沃斯(Butterworth)滤波器、切比雪夫(Chebyscheff)滤波器、贝塞尔(Bessel)滤波器及椭圆函数(Elliptic)滤波器。虽这些滤波器设计过程均已较为成熟,但无论哪种设计过程却均需要繁琐复杂的计算,或使用大型设计软件,因此不便于使用。Matlab[1]作为一种高性能数值计算和可视化的工程计算工具,其具有丰富的数学函数功能支持,并提供了丰富的用于模拟滤波器设计的函数 继续阅读

1、设计指标 用微带或带状线实现低通滤波器的一种相对容易的方法是用很高和很低特征阻抗的传输线交替排列的结构。这种滤波器通常称为阶跃阻抗(Stepped-Impedance)或高Z一低Z滤波器，由于它结构紧凑且较容易设计，所以比较流行。然而，它的电特性不是很好，故通常应用于不需要有陡峭截止响应的场合。 （1）具有最平坦响应（巴特沃斯）。 （2）截止频率为2 继续阅读

01 Sallen-Key滤波器 一、背景介绍 近期由于需要测试所搭建的高阻抗信号源放大电路，其中包括有低通滤波器，所以研究了 Sallen-Key topology[1] 相关滤波电路电路。如下是 Kennth A. Kuhn 在 2016 给出的 Sallen-Key Low-Pass Filter[2] 设想步骤；2002年 TI 给出的 Analysis of the Sallen-Key Architecture[3] 应用报告&#xff0 继续阅读

一阶数字低通滤波器传递函数为： ωc=2πfc ωc​为滤波截止角频率  :截止频率，单位： HZ 对低通滤波器进行离散化 一  后向差分法 变换公式为： s=(1−z−1)/Ts​ Ts：采样频率 将变化公式带入传递函数，可得差分方程： y(n)=(ωc​Ts​)/(1+ωc​Ts​)x(n)+1/(1+ωc​Ts​) 继续阅读

这个问题在互联网上以各种形式被问到，而且有一个简单的答案，常常被忽略或混淆： 简单回答： Keras Conv2D层在多通道输入(例如彩色图像)的情况下，将在所有颜色通道上应用滤波器，并将结果求和，生成等效于单色卷积输出图像。在 (1)您正在使用CIFAR图像数据集进行培训，该数据集由32x32颜色图像组成，即每个图像都是形状(32,32,3)(RGB=3个通道 继续阅读