一阶数字低通滤波器传递函数为：
ωc=2πfc
ωc为滤波截止角频率
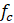:截止频率，单位： HZ
对低通滤波器进行离散化
一 后向差分法
变换公式为：
s=(1−z−1)/Ts
Ts：采样频率
将变化公式带入传递函数，可得差分方程：
y(n)=(ωcTs)/(1+ωcTs)x(n)+1/(1+ωcTs)y(n−1)
令a=(ωcTs)/(1+ωcTs)=
， 
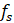：采样频率
若采样频率远大于截止频率，则 a
则1/(1+ωcTs)=1-a；整理得：
y(n)=ax(n)+(1−a)y(n−1)
其中：y(n)为本次滤波值，y(n-1)上次滤波值为， x(n)为本次采样值。
matlab程序：
clc;clear;close all;fc = 100;
fs = 500;
ts = 1/fs; % 采样周期
wc=2*pi*fc;s=tf('s');
sys=wc/(s+wc);
b=wc;
a=[1,wc];lowpass_filter = tf(b, a);%创建连续时间传递函数模型P=bodeoptions;%设置bode图的属性参数
P.FreqUnits = 'Hz';%单位hz
figure(1);
bode(lowpass_filter, P);
grid on;%显示轴网格线
title('lowpass\_filter\_Idesign');二 双线性变换法
传递函数
a=ωc,T采样频率
双线性变换法变换算子：
带入得：
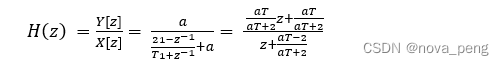
解得
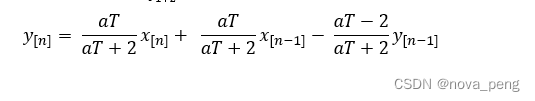
总结
截止频率越低，滤波越平滑，但并非越低越好，截止频率越低，信号延迟越大，这对于控制系统来说并非好事。
采样频率远大于截止频率时，两种变换滤波效果相差不大；采样频率与截止频率相差不大时，双线性变换滤波效果更好，通带内延迟低，阻带信号衰减幅度更快。
本文链接：https://my.lmcjl.com/post/7717.html
展开阅读全文
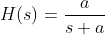
4 评论