文献综述
由Zhi-Wei Liu , Huazhou Hou , Yan-Wu Wang在2019年投的文章:Formation-containment control of multiple underactuated surfacevessels with sampling communication via hierarchical sliding mode approach,分析线性系统理论的应用。
本文的系统为欠驱动的水面舰艇模型系统:
此系统为非线性欠渠道驱动系统,系统运动学模型为:
本文中为了使系统稳定,使用了终端滑模理论:
当系统满足 时,状态x可以在有限时间内从任意的初始状态到达平衡点。
因此选择状态误差为状态x,滑模面为:
uie为欠驱动水面舰艇系统实际当前位置与期望位置的状态误差,
Vie为欠驱动水面舰艇系统的实际速度与期望速度的状态误差,然后利用李雅普诺夫直接法,设计李雅普诺夫函数为:
此李雅普诺夫函数正定,然后由李雅普诺夫直接法,带入设计的输入函数,可以证明此李雅普诺夫函数的导数为负定的,且为大范围稳定,则Si1、Si2可到达原点,那么由滑模理论,欠驱动的水面舰艇系统可以跟踪期望的轨迹。
另一篇是Chang-Duo Liang , Ming-Feng Ge , Zhi-Wei Liu , Guang Ling , Feng Liu作者的:
Predened-TimeFormationTracking Control of Networked Marine Surface Vehicles,
首先由图论的知识得到拉普拉斯矩阵:
和把矩阵:
由引理:
设计网络化水面舰艇系统的控制法则,系统的运动学和动力学模型为:
其中:
控制目标为在预定的时间内水面舰艇可以跟踪上期望的轨迹,其速度可以跟踪期望的速度,即:
设计此系统与期望的误差,根据引理,设定状态变量为:
李雅普诺夫函数为:
然后证明了其导数为负定:
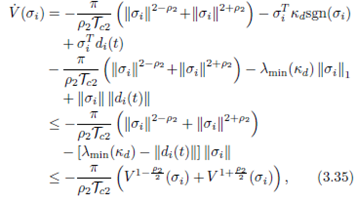
即达到引理1的条件,则设计的控制输入可以实现系统的预定时间跟踪期望轨迹和速度。
总结:目前研究的方向为多智能体的协调控制,大致就是设计各种智能体系统模型的控制法则,使得多智能体编队可以在实现各种目标任务,其主要用到了李雅普诺夫直接法来证明设计的控制法则使设定的状态变量收敛,这里的设定的状态变量一般为轨迹误差、速度误差,或者根据其他引理设计的一些函数。另外论文里设计大量的控制理论的基础知识,比如状态矩阵、图论、图论里的邻接矩阵、指数稳定等等,控制理论是我的研究方向的基础理论和工具,其作用和意义非常大。
注:转载使用请经过本人同意!
本文链接:https://my.lmcjl.com/post/11153.html

4 评论