输入输出样例
输入 #1
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
输出 #1
4这道题看上去可以说一点思路都没有(反正蒟蒻是这样的)
可以看到他的输入是无序的,我们先按照他们的北岸的编号来排个序。然后来画个小图:
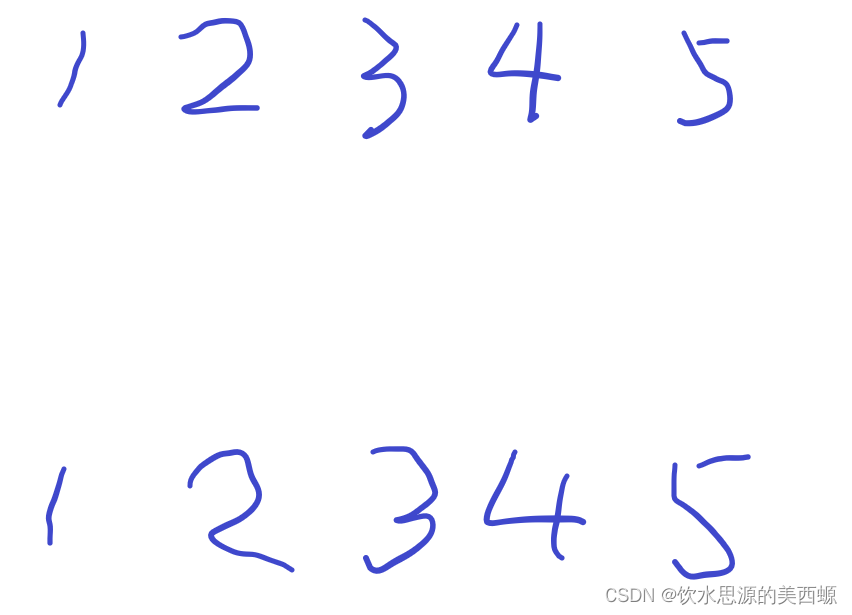
我们用这些数表示他的北岸和南岸
假设是这样的:
北岸1-南岸3
北岸2-南岸5
北岸3-南岸1
北岸4-南岸2
北岸5-南岸4
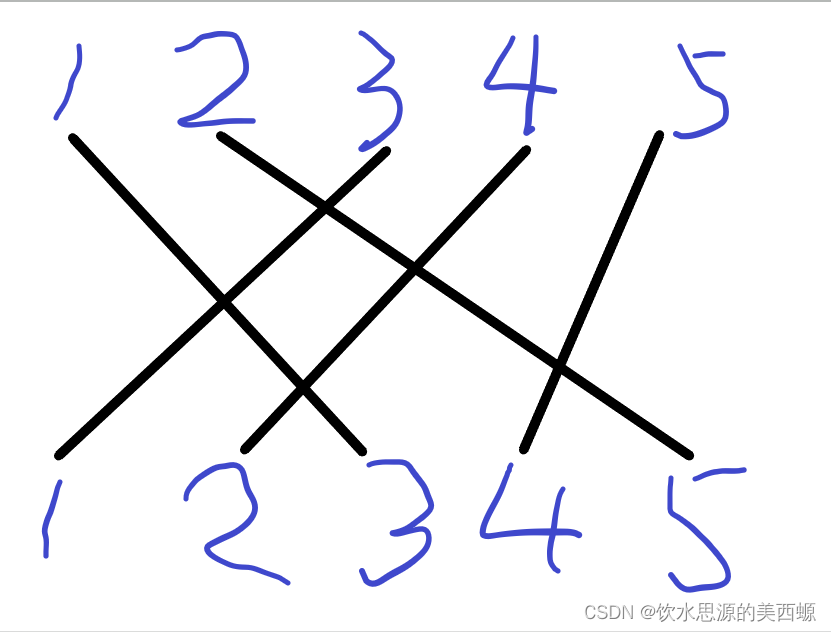
这个图有很多的交叉,所以我们不得不去舍去一些线。可以发现,把北岸1-南岸3和北岸2-南岸5舍去是最优解,这样能保留下3条边。
我们抽象一下,把上面的图的北岸排序后,南岸其实是这样的:
3 5 1 2 4
刚才做的,是把3和5舍去了,剩下的是1 2 4,也就构成了一个叫做“最长不下降子序列”
好的,那么问题就抽象成了:在北岸有序的情况下,南岸的最长不下降子序列
求最长不下降子序列,首先想到的是O(n^2)的做法,可是n<=200000,n^2超时了,只有50分
50分做法:
# include <iostream>
# include <cstdio>
# include <algorithm>
# include <cstring>
using namespace std;
# define int long long
int n,maxn=-1;
int f[200005];
struct node{int nor,sou;
}map[200005];
bool cmp(node x,node y){return x.nor<y.nor;
}
signed main(){scanf("%lld",&n);for (int i=1;i<=n;i++){scanf("%lld%lld",&map[i].nor,&map[i].sou);f[i]=1;}sort(map+1,map+1+n,cmp);f[0]=1;for (int i=1;i<=n;i++){for (int j=1;j<i;j++){if (map[j].sou<=map[i].sou){f[i]=max(f[i],f[j]+1);}maxn=max(maxn,f[i]);}}printf("%lld",maxn);return 0;
}(没啥可说的代码模板)
那么我们现在就要去优化,把j循环去了(最优)
还是画个小图,模拟下求最长不下降子序列的过程

这样一个序列,并创建一个数组,存储最长不下降子序列
首先,100加入子序列
再去考虑96,96如果加入子序列,100就会被踢掉,但96更小,所以保留96踢100
考虑334,他进入序列没问题
考虑25,他进入序列,就会把两个数都踢了,不划算,不要了
考虑162,他进来会把334踢了,可以
考虑131,他进来会把162踢了,没事
所以最后就是96 131
他这道题只问你最后的长度,具体的数不考虑,所以这样没问题
那么最后就用代码模拟这个过程就行
# include <iostream>
# include <cstdio>
# include <algorithm>
# include <cstring>
using namespace std;
# define int long long
int n,maxn;
int f[200005];
struct node{int nor,sou;
}map[200005];
bool cmp(node x,node y){return x.nor<y.nor;
}
int south[200005];
int left,right;
signed main(){scanf("%lld",&n);for (int i=1;i<=n;i++){scanf("%lld%lld",&map[i].nor,&map[i].sou);}sort(map+1,map+1+n,cmp);south[++maxn]=map[1].sou;for (int i=2;i<=n;i++){/*for (int j=1;j<i;j++){if (map[j].sou<=map[i].sou){f[i]=max(f[i],f[j]+1);}maxn=max(maxn,f[i]);}*/int ans=upper_bound(south+1,south+1+maxn,map[i].sou)-south;//寻找第一个>目标值的数 south[ans]=map[i].sou;if (ans>maxn){maxn++;}}printf("%lld",maxn);return 0;
}
本文链接:https://my.lmcjl.com/post/13203.html
展开阅读全文

4 评论