| 实验目的: 1.掌握单样本t检验、两样本t检验、配对样本t检验、单因素方差分析、多元回归分析的基本原理; 2.熟悉掌握SPSS软件或者R软件关于单因素、多因素方差分析、多元回归分析的基本操作; 3.利用实验指导的实例数据,上机熟悉以上3种方法(t检验、方差分析、多元回归分析)。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验内容: 1. 实验数据为专业学生核心课程成绩及实验指导中的数据; 2. 利用SPSS或者R软件上机实践单样本t检验、两样本t检验、配对样本t检验、单因素方差分析、多元回归分析(线性回归、二元logistics回归),解释结果; 实验数据 1.对八块油茶树进行测量,计单位面积株数为x1,每株果实量为x2,单位面积产油量为y,测得数据如下:
试建立y对x1,x2的线性回归方程,并进行检验。 2.试求一个厂家, 5个月中产品的广告费用与销售额之间的一元二次回归模型。其中,产品的广告费用与销售额的抽样数据为:
试建立销售额与广告费的一元二次回归模型,并检验判断是否有实际意义。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.现有15名不同程度的烟民的每日饮酒(啤酒)量与其心电图指标(zb)的对应数据。烟民的每日饮酒(啤酒)量与其心电图指标(zb)的对应数据
试建立拟合这些数据的模型。4.检验专业核心课程成绩某一门课程与75分是否有显著性差异; 某2门课程成绩差异是否显著 5. 检验以下数据的药物治疗效果是否有显著差异
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验前预习: 1. 单样本t检验、两样本t检验、配对样本t检验的基本原理为,软件操作步骤; 2. 单因素方差分析基本原理为,软件操作步骤; 3. 多元回归分析(线性回归、二元logistics回归)基本原理为,软件操作步骤。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 程序测试、运行结果及分析:
(检验专业核心课程成绩某一门课程与75分是否有显著性差异) 操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“比较平均值” à 选择“单样本t检验” à 拖动高代1至检验变量框 à 在检验值框输入75 à点击“选项” à 在置信区间百分比框输入95à 点击“继续”和“确定” 运行结果:
结果分析: T检验的p值是0.004,小于显著性水平0.05,拒绝原假设(即没有显著性差异)因此可以认为高代1成绩的总体均值与75分有显著性差异。 单样本t检验是利用总体的样本数据,推断总体均值与指定检验值之间是否有显著差异,也就是对总体均值的假设检验,注意其数据必须服从正态分布。(比如检验一批零件是否正常)
(某2门课程成绩差异是否显著) 操作步骤: 打开spss软件 à 在“变量视图”名称列分别输入成绩和科目类别 à 在科目类别的“值”框定义1为高代1,2为高代2 à 在“数据视图”分别将高代1和高代2的成绩复制到成绩列à 在科目类别列,高代1所对应的行输入1,高代2所对应的行输入2 à点击“分析”à 点击“比较平均值” à 选择“独立样本t检验” à 拖动成绩至检验变量框,科目类别拖动至分组变量框à 点击“定义组”并分别输入1和2à点击“选项” à 在置信区间百分比框输入95à 点击“继续”和“确定” 运行结果:
结果分析: 无论方差是否相等,其p值是都为0.990均大于显著性水平0.05,接受原假设(即没有显著性差异)因此可以认为高代1与高代2的成绩没有显著性差异。 两(独立)样本t检验就是利用两个总体的独立样本,推断两个总体的均值是否有显著性差异。注意两数据必须是独立的(比如检验两个行业的工资是否有显著性差异)
(学生考不同课程成绩是否由显著差异。) 操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“比较平均值” à 选择“成对样本t检验” à 拖动高代1和高代2至配对变量框 à点击“选项” à 在置信区间百分比框输入95à 点击“继续”和“确定” 运行结果:
结果分析: 由表知,t检验的p值为0.985大于显著性水平0.05,说明拒绝原假设出错的概率较大,所以选择接受原假设(即没有显著性差异),可以认为同一个学生考高代1和高代2成绩的没有显著性差异。两配对样本t检验就是利用两个总体的配对样本推断总体均值是否存在显著差异(比如检验两公司对同一个数据的评估是否有差异,或者同一个学生考不同科目成绩是否由显著差异。)注意数据必须是随机的。
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“比较平均值” à 选择“单样本ANOVA检验” à 拖动药物种类拖入因子框,将治愈天数拖入因变量框à点击“选项” à “确定”(注意填写数据时,一列为药物种类,一类为治愈天数,并将药物种类列填写1,2,3,4,5分别代表药物1,药物2,药物3,药物4,药物5) 运行结果:
结果分析: 单因素方差分析用于分析单个控制因素取不同水平时,因变量的均值是否存在显著性差异(比如分析不同种类机器的平均产量是否有显著性差异) 由结果可知,p值为0.014小于显著性水平0.05,所以拒绝原假设出错的概率小,拒绝原假设(没有显著性差异),可以认为不同药物种类的平均治愈天数有显著性差异。
现有15名不同程度的烟民的每日饮酒(啤酒)量与其心电图指标(zb)的对应数据。烟民的每日饮酒(啤酒)量与其心电图指标(zb)的对应数据
试建立拟合这些数据的模型。 操作步骤: 打开spss软件 à 在“变量视图”名称列分别输入心电指标和日吸烟量以及日饮酒量, à 在“数据视图”输入题目数据à点击“分析”à 点击“一般线性模型” à 选择“单变量” à 拖动心电指标至因变量列表框,日吸烟量和日饮酒量拖动至固定因子框à 点击“事后比较”并在显著性水平框输入0.05 à 点击“继续”和“确定” 运行结果:
结果分析: 多因素方差分析用于分析多个控制变量影响下的样本之间均值是否存在显著性差异(比如考察对纤维弹性的影响,多个因素是否有显著影响)由上表可知,日吸烟量因素的p值为0.251大于显著性水平0.05,接受原假设(没有显著影响),可以认为日吸烟量和心电指标没有显著性影响,同样日饮酒量的p值为0.297,其对心电指标也没有显著性影响。
对八块油茶树进行测量,计单位面积株数为x1,每株果实量为x2,单位面积产油量为y,测得数据如下:
试建立y对x1,x2的线性回归方程,并进行检验。 操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“回归” à 选择“线性” à 拖动x1和x2至自变量并且将y拖入因变量框 à 点击“确定” 运行结果:
结果分析: 从运行结果可知常量p=0.871>0.05及x2:p=0.359>0.05,说明其不显著,则每株果实量x2对产单位面积油量y没有影响;而x1:p=0.014<0.05,则说明其显著。 所以重新建立单位面积油量y与单位面积株树x1的回归方程得到结果:
此时,常量和x1的p值均小于0.05,说明其具有显著性,得到最终回归方程为 y=0.116x1+0.792
对回归方程进行显著性检验R和R方都大于0.7达到显著水平,说明其具有实际意义。
试求一个厂家, 5个月中产品的广告费用与销售额之间的一元二次回归模型。其中,产品的广告费用与销售额的抽样数据为:
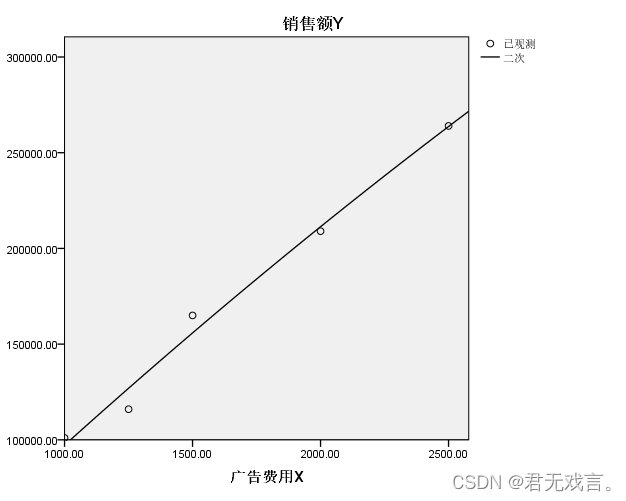
试建立销售额与广告费的一元二次回归模型,并检验判断是否有实际意义。 操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“回归” à 选择“曲线估计” à 拖动广告费和销售额分别自变量和因变量框 à模型框点击“二次项” à 点击“确定” 运行结果:
结果分析: 由表可知得到广告费x和销售额y之间的关系为: Y=132.910x-0.006x^2-29417 对方程进行显著性检验,其R方为0.988大于0.7说明其有极显著性,所以有实际意义 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 讨论: 1.T检验 单样本t检验是利用总体的样本数据,推断总体均值与指定检验值之间是否有显著差异,也就是对总体均值的假设检验,注意其数据必须服从正态分布。(比如检验一批零件是否正常)P小,拒绝H0的出错概率就小,所以拒绝,P大,拒绝H0出错的概率就大,所以接受 两(独立)样本t检验就是利用两个总体的独立样本,推断两个总体的均值是否有显著性差异。注意两数据必须是独立的(比如检验两个行业的工资是否有显著性差异) 两配对样本t检验就是利用两个总体的配对样本推断总体均值是否存在显著差异(比如检验两公司对同一个数据的评估是否有差异,或者同一个学生考不同科目成绩是否由显著差异。)注意数据必须是随机的。 2.方差分析 单因素方差分析用于分析单个控制因素取不同水平时,因变量的均值是否存在显著性差异 多因素方差分析用于分析多个控制变量影响下的样本之间均值是否存在显著性差异 3,回归分析 Logistic回归其本质就是非线性回归,应用于检验因果关系或者预测,其有三种变量类型 二分类(判断有和无) 有序多分类(满意 基本满意 不满意) 无序多分类(坐飞机 坐火车 坐高铁) |
本文链接:https://my.lmcjl.com/post/13495.html





4 评论