哈喽,大家好,我是赏月君,今天讲一下图论,废话少说,走起。
图由顶点( vertex, node )和边( edge)组成。顶点代表对象。在示意图中,我们使用点或圆来表示。边表示的是两个对象的连接关系。在示意图中,我们使用连接两顶点之间的线段来表示。顶点的集合是V、边的集合是E的图记为G =(V, E),连接两点u和v的边用e=(u, v)表示。
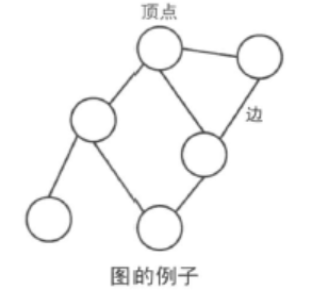
1.图的种类
图大体上分为2种。边没有指向性的图叫做无向图,边具有指向性的图叫做有向图。表示朋友关系的图(顶点表示人、边表示朋友关系的图)和路线图是无向图。表示数值的大小关系的图(顶点表示数值、A>B时从A向B连一条边得 到的图)和流程图是有向图。
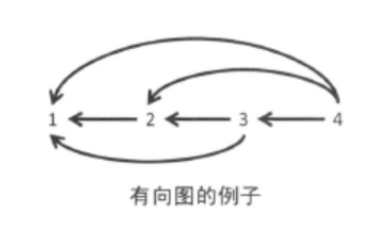
我们可以给边赋子各种各样的属性。比较具有代表性的有权值( cost)。边上带有权值的图叫做带权图。在不同问题中,权值可以代表距离、时间以及价格等不同的属性。
2.无向图的术语
两个顶点之间如果有边连接,那么就视为两个顶点相邻。相邻顶点的序列称为路径。起点和终点重合的路径叫做圈。任意两点之间都有路径连接的图叫做连通图。顶点连接的边数叫做这个顶点的度。
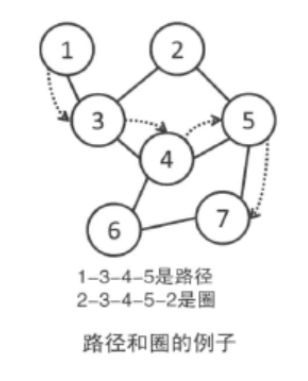
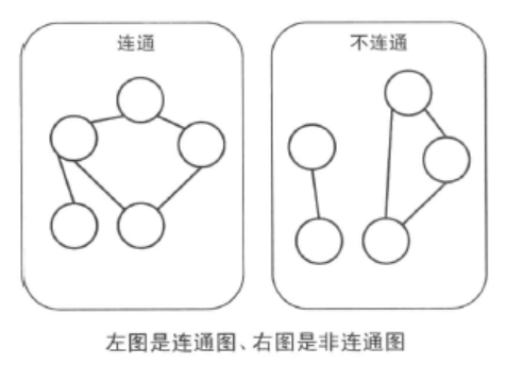
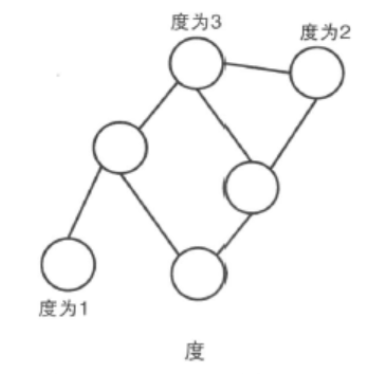
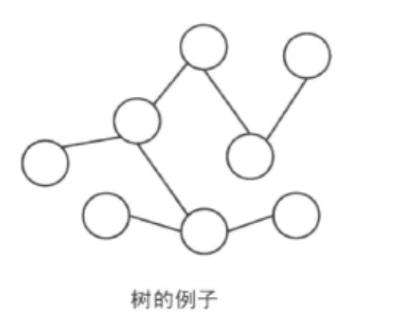
没有圈的连通图叫做树( tree),没有圈的非连通图叫做森林。一棵树的边数恰好是顶点数-1。反之,边数等于顶点数-1的连通图就是一棵树。
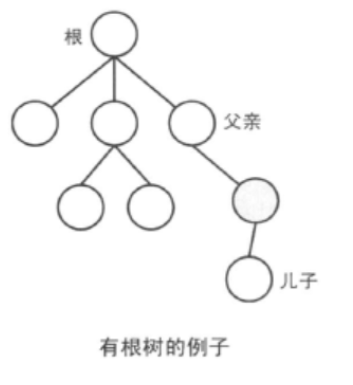
如果在树上选择一个顶点作为根( root),就可以把根提到最上面,而离根越远的顶点越往下安排其位置。这样的树叫做有根树。不过,对于无根树,有时选择适当的顶点作为根使之变成有根树,可以使问题得到简化。如果把有根树看作家谱图,则可以在顶点之间建立父子关系。也可以认为这是给边加上了方向。
3.有向图的术语
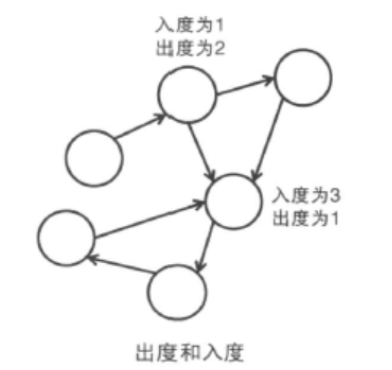
以有向图的顶点v为起点的边的集合记作E+(v), 以顶点v为终点的边的集合记作E_(v)。|E+(v)|叫做v的出度,|E_(v)|叫做边的入度。
没有圈的有向图叫做DAG ( Directed Acyclic Graph)。例如,让我们用顶点表示整数,n能整除m时从n向m连一条边的图,这就构成一个DAG。 像下图一样, 在DAG中我们可以给顶点标记一个先后顺序。
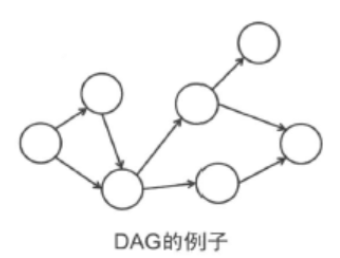
对于每个顶点我们给它一个编号,第i号顶点叫做vi。那么存在从顶点vi到顶点vj的边时就有i<j成立,这样的编号方式叫做拓扑序。
如果把图中的顶点按照拓扑序从左到右排列,那么所有的边都是从左指向右的。因此,通过这样的编号方式,有些DAG问题就可以使用DP来解决了。求解拓扑序的算法叫做拓扑排序。
图的表示
为了能在程序中对图进行处理,需要把顶点和边用具体的数据结构存储下来。在图的表示方法中,比较具有代表性的有邻接矩阵和邻接表。需要注意的是,两种表示方法都有各自的优缺点,根据问题的不同,使用不同的存储方式可能会影响算法的时间复杂度。接下来,记顶点和边的集合为V和E,|V|和|E|表示顶点和边的个数。另外,在V中,顶点被编号为0~|V|-1。
1.邻接矩阵
邻接矩阵使用|V|x|V|的二维数组来表示图。g[i][j]表示的是 顶点i和顶点j的关系。
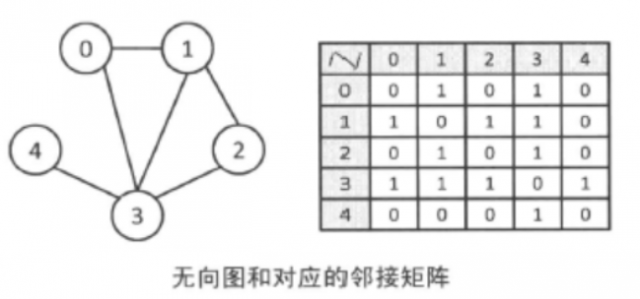
由于在无向图中,只需知道“顶点i和顶点j之间是否有边连着”这样的信息,因此如果顶点i和顶点j之间有边相连,那么g[i][j]和g[j][i]就设为1,否则设为0。这样就可以表示一个无向图了。
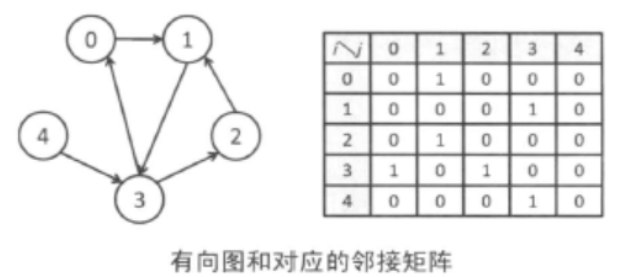
由于在有向图中,只需要知道“是否有从顶点i发出指向顶点j的边”这样的信息,因此如果顶点i有一条指向顶点j的边,那么g[i][j]就设为1,否则设为0。这样就可以表示一个有向图了。 有向图与无向图不同,并不需要满足g[i][j]= g[j][i]。
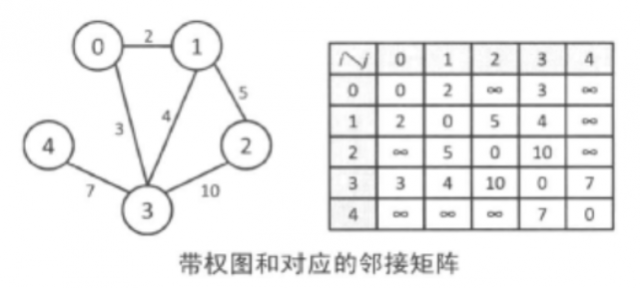
在带权图中,8[i][j]表示的是顶点i到顶点j的边的权值。由于在边不存在的情况下,如果将g[i][j]设为0,就无法和权值为0的情况区分开来,因此选取适当的较大的常数INF (只要能和普通的权值区别开来就可以了),然后令g[i][j]=INF就好了。当然,在无向图中还是要保持g[i][j]=g[i][j]。在一条边上有多种不同权值的情况下,定义多个同样的|V|x|V|数组,或者是使用结构体或类作为数组的元素,就可以和原来一样对图进行处理了。
使用邻接矩阵的好处是可以在常数时间内判断两点之间是否有边存在,但是需要花费O(|V|²)的空间。在边很少的稀疏图里十分浪费。例如,如果图是一棵树,因为边数只有|V|-1条,所以数组g绝大部分的元素都变成了0。在|V|达到1000000时,即使g的每个元素只需要1个字节的空间,整个数组也需要1TB才能存下。
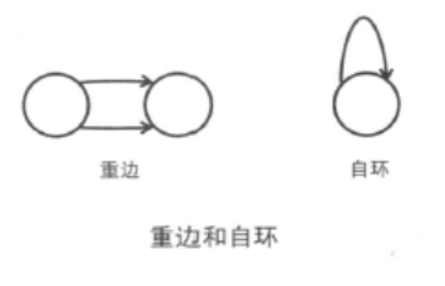
此外,两点之间有重边或者某个顶点有自环(参照下图)的情况需要特别注意。在无权图中,只需要设g[i][j]为顶点i到顶点j的边数即可,但是在带权图中却无法这样。大部分情况下,只需要保存权值最小(最大)的边就可以了,所以在这种情况下可以无视其他的边。必须保存所有的边时,可以使用邻接表。
2.邻接表
用邻接矩阵表示稀疏图会浪费大量内存空间。而在邻接表中,是通过把“从顶点0出发有到顶点2, 4, 5的边”这样的信息保存在链表中来表示图的。这样只需要O(|V|+|E|)的内存空间。
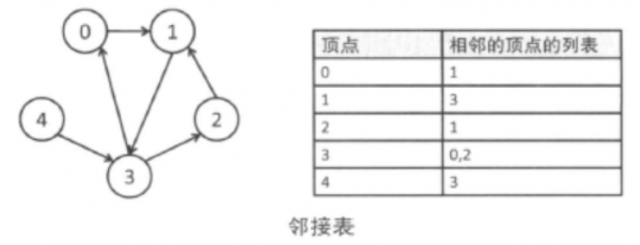
事实上,实现邻接表的方式多种多样,每个人的写法可能都有所不同。下面是邻接表的一种实现方式。输人数据如下所示。
3 3 //(顶点数边数)
0 1 //(有一条0到1的边)
0 2 //(有一条0到2的边)
1 2 //(有一条1到2的边)
vector<int> G[MAX_V];
int main(){int V,E;scanf("%d %d",&V, &E);for(int i=0;i<E;i++){//从s向t连边int s,t;scanf("%d %d",&s,&t);G[s].push_back(t);//如果是无向图,则需要再从t向s连边}return 0;
}
本文链接:https://my.lmcjl.com/post/13859.html

4 评论