一、图的分类
有向图:各个顶点之间的路径存在方向
无向图:各个顶点之间的路径不存在方向
带权图:各个顶点之间的边上有权值,这个权值可以是路径的长度,实际问题中可以是路的长度、走这条路花费的成本等。
二、一个在线作图的网站
https://csacademy.com/app/graph_editor/
三、带权图的权重邻接矩阵
若途中两点之间有边,则矩阵对应位置处的值为该边的权值。
注意:如果图是有向图,则要注意箭头的方向,这个时候,权重邻接矩阵就不是关于主对角线对称的了。
如果不带权重,这个时候,如果两点之间有边,则矩阵对应位置处填1,没边则填0。
总而言之,邻接矩阵研究的是顶点之间的关系,矩阵的行向量和列向量都是顶点。
四、图的关联矩阵
与邻接矩阵不同,图的关联矩阵研究的是边和顶点之间的关系。在图中,如果某条边和某两个点点是相邻的,则在矩阵的对应位置填入1,否则填入0。
在这里就要介绍一下边和顶点相邻的概念:如果一个顶点是某条边的两个端点中的一个,那么,这个顶点和这条边就称为相邻。
五、迪杰斯特拉算法
1、该算法的核心思想是将所有顶点分为两个集合,一个集合是已经遍历过的点,另一个集合是没有遍历过的点。通过不断地寻找路径的最小值,最终找到最短路径。具体理解看下面视频(前五分钟):https://www.bilibili.com/video/av54668527
2、该算法的一个显著缺点:如果图中出现了负权重,则不能用该算法来求解。
六、贝尔曼-福特算法
为了解决迪杰斯特拉算法不能处理负权重的缺点,可用贝尔曼-福特算法。
但是,贝尔曼-福特算法同样不能处理含有负权回路的图。
负权回路:如果在一个图中存在一个环,这个环的各权值加起来结果是小于零的,那么这个回路就称为负权回路。
注意:在无向图中,因为边不存在方向,因此一条边即可看成一条回路,所以,贝尔曼-福特算法不能处理带有负权权重的无向图。
具体理解看下面视频:https://www.bilibili.com/video/av43217121
六、图论问题的matlab实现
1、graph函数
graph(s,t,w):可在 s 和 t 中的对应节点之间以w的权重创建边,并生成一个图,例如:
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);使用上述命令,即可生成图G,s和t中对应位置的两点之间就会生成一条边,边的权值就是w中对应位置出的数字。
为了方便理解,使用plot函数将上述图画出来,如下图:

画图的命令为:
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 画出的图中会有坐标轴,实际上,这个坐标轴并没有什么用处,我们可以使用如下命令将坐标轴去掉:
set( gca, 'XTick', [], 'YTick', [] ); 2、使用如下命令可以返回两点之间的最短路径:
[P,d] = shortestpath(G, 9, 4)p返回的是最短路径经过的点,d返回的是最短路径的长度,9和4是两个参数,意思是9和4之间的最短路径。
以上面的图为例,使用上述命令:

3、在图中高亮我们的最短路径
% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r') %对这个变量即我们刚刚绘制的图形进行高亮处理(给边加上r红色)4、使用如下命令可以返回图中任意两点之间的距离(结果是一个矩阵)
D = distances(G)以上面的矩阵为例,生成的矩阵如下:

5、出给定范围内的所有点
使用如下命令即可实现找出给定范围内的所有点:
[nodeIDs,dist] = nearest(G, 2, 10)其中,2和10是两个参数,意思是找到以2这个点为中心,距离10以内的所有点。
返回的结果中,nodeIDs 是距离为10以内的点的标号,dist为对应的距离。
例如:
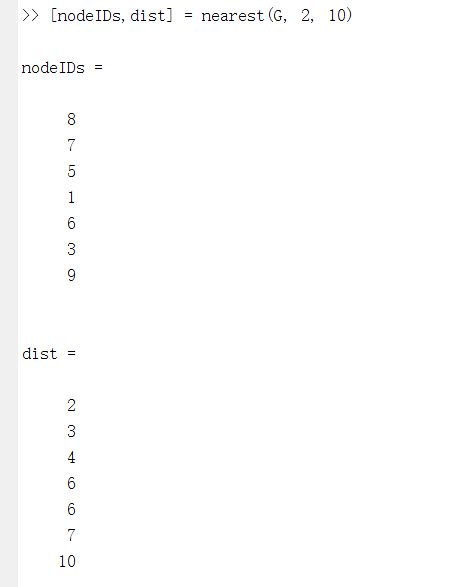
表示,以2这个点为中心,10以内的点有: 8 7 5 1 6 3 9
对应的距离是 2 3 4 6 6 7 10
本文链接:https://my.lmcjl.com/post/13931.html

4 评论