| 实验目的: 1.掌握聚类分析及判别分析的基本原理; 2.熟悉掌握SPSS软件进行聚类分析及判别分析的基本操作; 3.利用实验指导的实例数据,上机熟悉聚类分析及判别分析方法。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验前预习: 1.聚类分析及判别分析的基本原理; 2.SPSS软件进行聚类分析及判别分析的基本操作及结果解释。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验内容: 1. 为了研究世界各国森林、草原资源的分布规律,共抽取了21个国家的数据,每个国家4项指标,原始数据见下表。试用该原始数据对国别进行系统聚类和K-均值聚类(分3类)分析。
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. 从不同地区采集了七块花岗岩,测其部分化学成分如下表:
试作如下分析:
3. 研究团队调查了20个品牌的电视机,记录了它们的市场定位(G):1.高端市场;2.中端市场;3.低端市场;质量评估得分(Q),功能评估得分(C)和价格(P)。如果一个全新的品牌被推出,其中Q=8.0,C=7.5,P=65,它的市场定位应如何?试用判别分析解决这个问题。
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 程序测试、运行结果及分析:
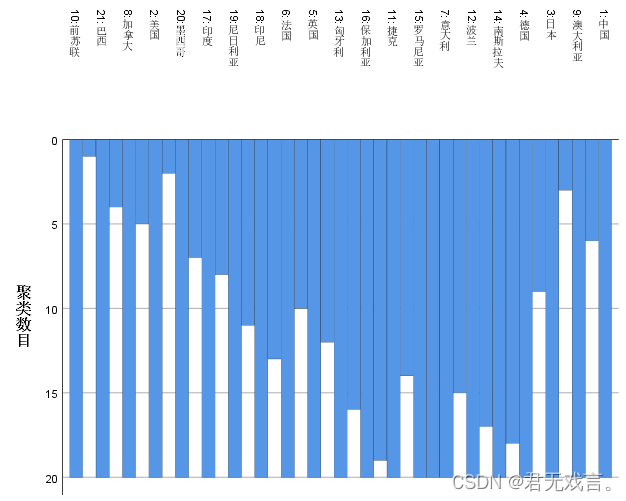
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“分类” à 选择“系统聚类” à 拖国别至个案标注依据à 其余拖入变量框à点击“图” à勾选“谱系图”à 点击“继续”和“确定” 运行结果:
结果分析: 对于冰柱图,自下而上的观察进行分类,美国和墨西哥之间的冰柱对应的分类数是三,所以分类为{前苏联},{美国,加拿大,巴西}其余为一类。 对于谱系图分成三类则为{前苏联},{美国,加拿大,巴西}其余的为一类。 聚类分析就是按照相似性把对象进行分类的方法。
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“分类” à 选择“系统聚类” à 拖国别至个案标注依据à 其余拖入变量框à点击“图” à勾选“谱系图”à点击“方法” à将聚类方法修改为“最近邻矩阵”或者“最远邻矩阵”à将区间框改为欧氏距离 à点击“继续”和“确定” 运行结果:
结果分析:同上一结果分析
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“分类” à 选择“系统聚类” à 拖国别至个案标注依据, 其余拖入变量框à 将聚类改为变量à点击“图” à勾选“谱系图”à 点击“继续”和“确定” 运行结果:
结果分析:略
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“分类” à选择“描述统计”并选择“描述” à 勾选“将标准化值另存为变量”à点击“确定” 选择“K-均值聚类” à 拖国别至个案标注依据à 标准化的数据拖入变量框à将聚类数改为3 à点击“选项”勾选统计框所有选项à 点击“继续”和“确定” 运行结果:
结果分析: 由方差分析表的p值可以判断出几个变量对分类的都是显著的,最后可以通过表可以知道三类则为{前苏联},{美国,加拿大,巴西}其余的为一类。
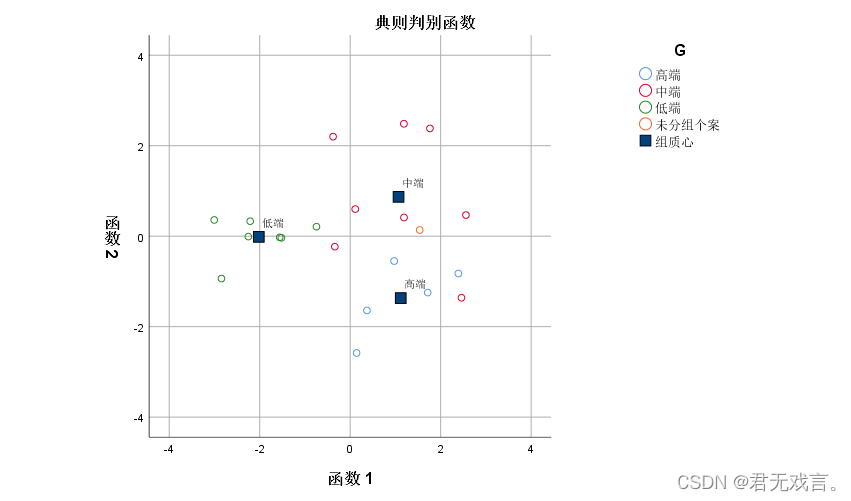
操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“判别式” à 将分组变量拖入框中并且点击选择范围1到3 à 拖其余名称至自变量à 点击“统计”并勾选“费歇尔” à在“分类”中点击“合并组”和“个案结果” à勾选“谱系图”à 点击“继续”和“确定”其余拖入变量框à点击“图” à勾选“谱系图”à 点击“继续”和“确定” 运行结果:
结果分析: 由第一个图可知,判定没有分组的数据为中端产品,即橙色的小圆圈离中端质心最近。 由第二个图可知,判别分析的正确率为百分之九十 由第三个图可知高端,中端,低端产品的分类函数分别为: Y1=13.022x1+4.367x2-0.332x3-60.635 Y2=11.004x1+3.886x2-0.136x3-52.853 Y3=9.279x1+2.115x2-0.165x3-29.854 代入数据Q,C,P分别为x1,x2,x3得到y2的绝对值最小,所以判别未知电视为中端产品 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 讨论: 1.判别分析与聚类分析的区别: (2)判别分析对(样本)个体进行分类,必须事先知道事物的类别,也知道应分几类,并已取得各类样品的观测数据,在此基础上根据某些准则建立判别式,然后对末知样品进行判别分类,它需要历史资料去建立判别函数。 (3)聚类分析可以对样本或指标进行分类,而判别分析只对样本进行分类。 (4)判别分析与聚类分析常常在一起使用:通过聚类分析首先确定出几个类型,对难以分类的样品再使用判别分析,确定其类别归属。 2.总结: 1.判别分析方法是按已知所属组的样本确定判别函数,制定判别规则,然后再判断每一个新样品应属于哪一类。 |
本文链接:https://my.lmcjl.com/post/1829.html





4 评论