上一章虽然已经能够将纹理碎片化,但是固定一条边,然后依次匹配第三个顶点的作法是无法适用于凹多边形的。
作为一个阿里眼里的菜逼,之前想着这个算法应该很简单,结果网上的各种转载也没找到个说清楚的文章,所以我将算法设计出来并实现了。本章将说一说如何“肢解”凹多边形。注意,这里仅仅是凹多边形,而不是形套洞,洞套形的套娃式复杂多边形,肢解那种多边形的算法相对更为复杂。而且最关键的,这种多边形的描述方式和无洞多边形是不可能一样的,外加目前我也只有一点想法,所以这方面的算法未来能实现出来再说吧。
使用cocos2dx实现碎片炸裂 P2(凹多边形的三角切割算法)(修订1)_zerozerg2006的博客-CSDN博客_凹包算法
回归正题。相信有兴趣来看这篇文章的朋友肯定知道什么是凸多边形与凹多边形的吧。。。。

直观形象我相信大家都有,但为了方便算法设计以及代码实现,我将多边形的定义抽象成了一个点序列,并且额外增加了一些约束。
定义1多边形:一个满足如下性质的点序列,元素为一个多边形的所有顶点坐标,按照逆时针顺序排列。而定义一个多边形是凹是凸,则可以使用上述定义。
定义2取多边形里的任意一个点A,令A按顺序往后的点为B和C(若已到序列尾部,则从头取),若向量AC一定在向量AB的逆时针方向,则此多边形为凸多边形,否则为凹。定义2用图去看就很容易明白,右侧中ATB三个点,不满足定义,所以这是一个凹多边形。(这个定义只是为了规范说法,对我们的算法没有用)
至于如何去判定方向,我们使用了向量叉乘这个方法。叉乘是将两个三维向量进行运算,然后获得一个三维向量。其方向为垂直于两个构成的平面,长度为两者向量长度之积乘以夹角的正弦值。
而正弦值比较好的一点是,如果夹角为0~pi,则为正,-pi~0则为负,正好满足我们用于判断旋转方向的需求。叉乘的运算公式大家可以去网上查,我就不赘述了(截图太麻烦……)
因为我们这里是2D游戏,所以可以认为所有向量的z分量为0,叉乘的结果最后就被退化为(0, 0, |A|*|B|*sina) = (0, 0, x1*y2 - x2*y1)。当z分量为正时,则为逆时针,为负时为顺时针。
(PS,cocos2dx中已经帮我们为Vec2定义了cross运算。)
另外,我们还需要准备一个判断点是否在三角形内的方法,或者说定义。(注意,这里只是三角形)
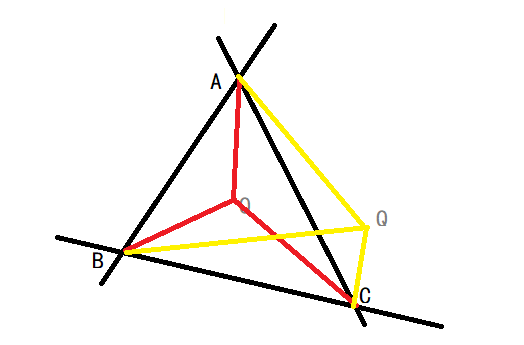
定义3若我们有一个满足定义1的三角形ABC,如果一个点P,其与所有顶点A与构成的向量AP,A与顺序顶点B构成的向量AB,AP在AB的逆时针方向或者同方向,则点P处于三角形内部,否则为外部。按照定义3,我们可以严谨的说P在三角形ABC内,而Q在三角形ABC外。
准备工作都完成后,就可以开始准备算法了。算法的核心思路,是为所有的边找到一个使用它的三角形。
输入,定义1的多边形点集S。将顶点的索引号以此存入一个容器List中只要List容器的大小大于等于3取List中的第一,第二个索引号Index1, Index2,按照索引号取到顶点P1,P2,并构成一条边P1P2。按顺序遍历List,直到遇见第一个点Q,使得P1Q是在P1P2的不为顺时针方向。(可以在逆时针方向,也可以共线,甚至是可以共点)如果Q与P1是同样的点,则移除P1,P2,回到循环开始。否则 1.如果P1PQ在P1P2的逆时针方向2.并且List中没有任何一个点处于三角形P1P2PQ中。
------修订线--------2.且另外的两条边不与多边形的其他边相交(可以很容易想到,这个条件强于之前的条件2)
--------------------则P1P2PQ是我们将要切割的一个三角形,将其加入我们的结果列表中然后如果IndexQ,为List的第三个索引号,则将Index2从List中移除如果IndexQ为最后一个索引号,则将Index1移除其他情况,则将Index1放到List的尾部,将头部第一个元素改为IndexQ返回结果列表这里进行以下简单“证明”,显而易见的,对于多边形,无论其凹凸,我们都可以将三角形的至少一条边,作为切割三角形的边,并且每一条边必然要使用一次且有且一次。证明很简单,反证法即可,如果存在不用的边,那该边的相邻的区域将没有被切割。而如果使用过多次,由于我们的图形是封闭多边形,所以边的两侧只会有一边属于多边形内部,所以如果多次计算同一条,则内部区域会被额外计算。
由于算法切割的三角形,其顶点使用了定义1的顶点列表,那剥离掉被切割三角形剩下的部分,可以将切口作为新的边,对顶点进行简单的调整,则仍然可以满足定义1。因此不停的进行分割顶点数小于3,也即是无法构成一个封闭图形,既算是算法完成。使用类似数学归纳法的方式我们可以“证明”算法可以将任意的定义1的多边形切割成三角形。
因为我们的算法是通过连结多边形顶点,然后切割三角形,所以只要是按照这种操作方式的最后的结果一定是合法的,但不一定是最优的。对于三点共线这种特殊情况我们的算法是可以兼容的。因为三点共线只是会将本来只需要切割成一个三角形的情况,额外切出多个三角形,但切出的图形并非错误的,所以这是一条优化项,但并不是必须的,因为优化会涉及到额外的判断(我们的第三个点可不一定是相邻的第3个点)。如果想省事不去优化也没啥问题,毕竟这是生产,而不是竞赛(这种问题的竞赛测试数据,绝逼会有一个超长的共线点序列)。
由于三角形的顶点选择的是多边形中的顶点,所以为了让算法更简便,我们进行了分类讨论用以维护我们的多边形定义(如果是数学来描述,就直接是删个点加个点,显然不适合组织数据建构进行编码。)
在定下了一条边以后,第三个顶点会有如下几个情况
1.是顺着的下一个顶点,如下图三角形BCD,显然我们只需要将顶点C去掉,形状就切割了。所以这种情况下,删除第二个顶点。
2.是序列的最后一个顶点(或者说,是我们第一个顶点的上一个顶点),如三角形JAB,那我们需要删掉顶点A,也就是第一个顶点。
3.除了1,2外的顶点,如三角形BDF(BD是在切割了BCD新生成的边),这种选择只用到了一条边,而非之前的两条边,这样产生的边会将我们的多边形的隔开,只剩下顶点链接,不过这并不破坏我们多边形的定义。那如何维护我们的序列呢,简单的做法,我们只需要将使用的顶点F插入到第一个与第二个之间就可以了。当然,为了方便编码与处理,我们可以将第一个顶点移动到List的尾部,然后在List头部插入这个点。
4.除了以上三种情况,我们的算法还会产生一种特殊情况,就是第三个点和第一个点是一样的。假如算法已经切掉ABJ,BCD,BFD,然后接下来切掉DEF,那FE的下一个顶点将会是F。合理的操作,我们可以连续移除这两个顶点。

使用cocos2dx实现碎片炸裂 P2(凹多边形的三角切割算法)(修订1)_zerozerg2006的博客-CSDN博客_凹包算法
我们使用上面的输入来走一遍算法流程。
初始化,List有(ABCDEFGHIJ),Result(),初始边为AB边。
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ |
扫描List,会发现除了J以外,所有顶点都是在顺时针方向,故取ABJ,满足条件2,故删除A,第一条选择下一条
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
下一个满足的顶点是D,满足条件1,故删除C,新的边为BD
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
| 3 | BD | BDEFGHIJ | JAB BCD |
BD为边,发现E虽然是逆时针方向,但是显然F会被包在三角形BDE中,所以排除,选择下一个顶点F,满足条件3,将F插入到BD之间,将B移动到末尾,新的边则为DF
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
| 3 | BD | BDEFGHIJ | JAB BCD |
| 4 | FD | FDEFGHIJB | JAB BCD BDF |
显然下一个是FDE,去掉D,边变为FE
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
| 3 | BD | BDEFGHIJ | JAB BCD |
| 4 | FD | FDEFGHIJB | JAB BCD BDF |
| 5 | FE | FEFGHIJB | JAB BCD BDF FDE |
下一个点位F,与第一个顶点是同一个,满足条件4,直接删除这条边的两个顶点,下一条边为FG
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
| 3 | BD | BDEFGHIJ | JAB BCD |
| 4 | FD | FDEFGHIJB | JAB BCD BDF |
| 5 | FE | FEFGHIJB | JAB BCD BDF FDE |
| 6 | FG | FGHIJB | JAB BCD BDF FDE |
剩下来都是是第一种情况,所以不赘述了,直接见表格
| Step | Edge | List | Result |
| 1 | AB | ABCDEFGHIJ | |
| 2 | BC | BCDEFGHIJ | JAB |
| 3 | BD | BDEFGHIJ | JAB BCD |
| 4 | FD | FDEFGHIJB | JAB BCD BDF |
| 5 | FE | FEFGHIJB | JAB BCD BDF FDE |
| 6 | FG | FGHIJB | JAB BCD BDF FDE |
| 7 | FH | FHIJB | JAB BCD BDF FDE FGH |
| 8 | FI | FIJB | JAB BCD BDF FDE FGH FHI |
| 9 | FJ | FJB | JAB BCD BDF FDE FGH FHI FIJ |
| 10 | FB | JAB BCD BDF FDE FGH FHI FIJ FJB |
如此一来,我们就将一个多边形切割成了若干个三角形的组合。
========================修订============================
之前的算法有一个很严重的缺失,我们可以看一下下面这张图。

如果以右下角的点A为起点执行算法,很显然,我们扫描到的第一个顶点是K,因为K在AB的逆时针方向,并且AKB中没有包含任何顶点。
但是显然,分割ABK是不合法的,三角形的一部分是没有在多边形里的。可选点应该是L。第一版算法没有考虑这种情况,所以在解析这一张图的时候,不是crash,就是无限死循环了,查了很久才发现这么一个错误。
那错误找到了,我们应该怎么去解决呢?其实很简单,如果待定三角形的三条边不与多边形的边相交就可以了。而且如果满足三角形中存在一个顶点,那一定满足至少两条边与待定三角形相交。所以可以直接替换原来的判定条件。
所以我们要找到判断相交的方法。
其实方法很简单,如果线段CD的顶点C,D分别在线段AB的两端,而线段AB的顶点A,B分别在线段CD的两边,那AB与CD就是相交的。配合上叉积,就很容易写出相应的判断函数。(证明我没有去想,所以不写了,思路估计可以通过解析几何的方式求证交点的存在性,或者使用向量的投影)
另外每一次都对相交判断会非常冗余,我们的顶点并不会变化,所以可以先预处理出线段之间是否相交,之后就可以直接用了(但是却额外需要一个N^4的存储空间,因为我们会为算法里的多边形产生新的边)
========================================================
需要补充说明的是,我们可以从任意一个顶点开始我们的算法,最后切割的三角形也并非是一定的,数量上也并不是一定是相同的,也不一定是最少的。但结果一定是对的。
算法的复杂度是标准的O(N^2) O(N^3),如果是凸多边形,则是O(N)。凸多边形为O(N^2)
遍历边N,扫描待定点N(凸多边形扫描的第一个点就是目标点,所以为1),判断构成三角形是否合法N
通常来说,速度肯定够了(你要给几千几万条边,还是奇奇怪怪的形状用这个算法当我没说,毕竟这是生产用的算法,不是科研用的),当然很可能有更快的方法,我就不去想了。反正我都被阿里鄙视成对cocos2dx一点都不了解的菜逼了。
最后的最后,切出的三角形最好也能够按照定义1的方式去管理和存储,至于什么用,你猜……

本文链接:https://my.lmcjl.com/post/7374.html

4 评论