个人原创笔记，转载请附上本文链接。
拉格朗日对偶性其实也没有那么难理解，在我梳理过后你会发现也就是那一回事罢了。
原始问题 P
我们的 原始优化问题 表述出来就是：在 
把 
原始问题使用数学语言表达形式见下图。
拉格朗日极小极大问题 P'
我们首先引入了拉格朗日函数。函数见图片中 公式② 。
我们提出的 拉格朗日极小极大问题：希望在
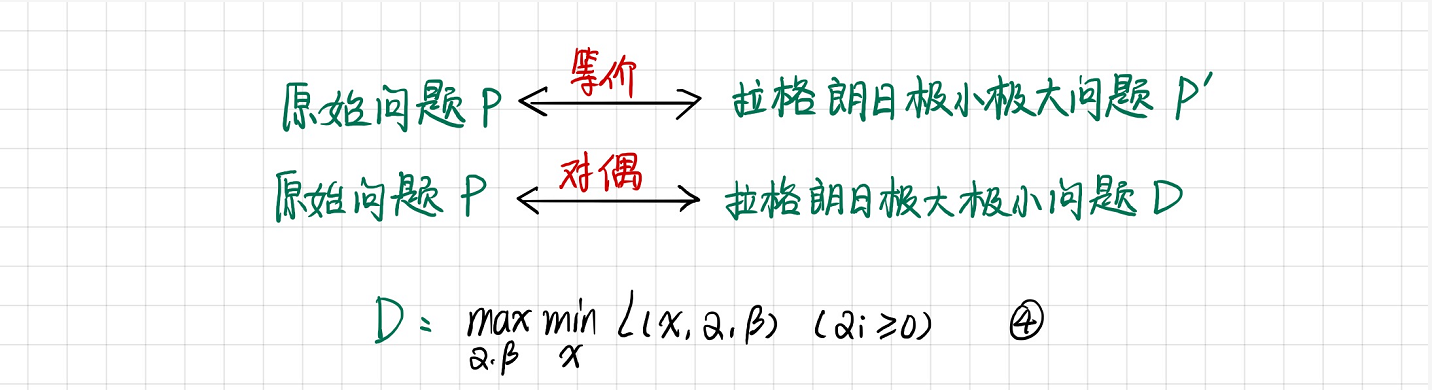
通过上面证明，我们发现，我们所研究的 原始问题 P 实际上就是与 拉格朗日极小极大问题 P' 等价的（也就是他们的解都是相同的）。我们只要记住这一点即可！
拉格朗日极大极小问题 D
这时候，就出现了 “对偶” 的概念了。拉格朗日极大极小问题D 就是 拉格朗日极小极大问题 的对偶问题，也即是，拉格朗日极大极小问题D 就是 原始问题 的对偶问题。（因为原始问题 P 实际上就是与 拉格朗日极小极大问题 P' 等价的）
别被绕晕了哈！其实不难的。
拉格朗日极大极小问题的表达式见下图 公式④。
探究 d* 与 p* 之间的关系
我们通过对
什么时候 d* = p* ？
-
-
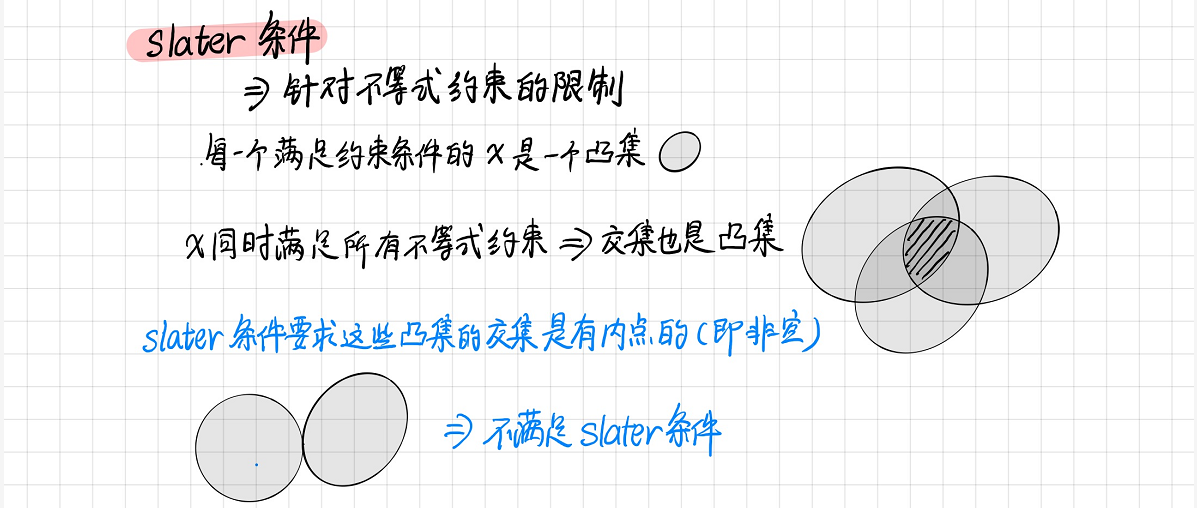
只有在这两个条件下才满足强对偶性！
KKT条件
当问题满足强对偶性时，我们就可以利用KKT条件，列出下面的方程组求解。
总结
本文链接：https://my.lmcjl.com/post/7854.html
展开阅读全文
4 评论