转载于https://www.cnblogs.com/gccbuaa/p/7357159.html
机器学习之深入理解SVM
在浏览本篇博客之前,最好先查看一下我写的还有一篇文章机器学习之初识SVM(点击可查阅哦)。这样能够更好地为了结以下内容做铺垫!
给定训练样本集D=(x1,y1),(x2,y2),......(xm,ym),y∈−1,+1,分类学习最主要的想法就是基于训练集D在样本空间中找到一个超平面。将不同类别的样本分开。
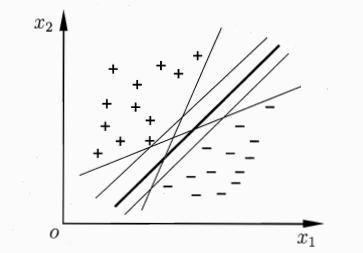
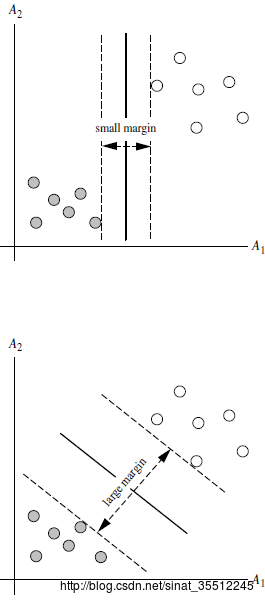
可是正例如以下图所看到的。能将训练样本分开的超平面可能有非常多。那我们应该选择哪一个呢?
直观上看,我们应该去找位于两类训练样本“正中间”的超平面,也就是样本点与直线的距离最大那条直线。由于该超平面对训练样本局部扰动的容忍性最好。
在样本空间中,超平面可用例如以下方程来描写叙述:
wTx+b=0,
当中w=(w1,w2,...wd)为法向量,决定了超平面的方向;b为位移项。是超平面与远点之间的距离。
显然超平面可由法向量w和位移b唯一确定。
一般来说,一个点距离超平面的距离d的大小能够表示分类预測的确信程度。在超平面wTx+b=0确定的情况下,
d=|wTx+b|||w|| (1)
当中。||w||为w的范数。
当点A表示某一实例xi,其类标记为yi=+1。点A与超平面的距离记作di,那么
di=wTxi+b||w|| (2)
当点A表示某一实例xi,其类标记为yi=−1。
点A与超平面的距离记作di。那么
di=−wTxi+b||w|| (3)
一般地。点xi与超平面的距离是
di=yiwTxi+b||w|| (4)
公式(4)也被称为超平面关于样本点xi的几何间隔。
最大间隔分离超平面
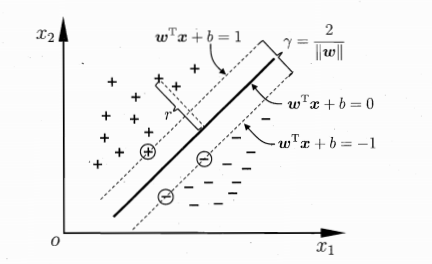
如上图所看到的,距离超平面近期的这几个训练样本点被称为支持向量。两个异类支持向量(即分别位于超平面两側的点)到超平面的距离之和为
d=2||w|| (5)
上面(5)的d称为间隔(margin)。
要求得最大间隔(即最大化2w),就是要满足:
显然。为了最大化间隔,仅需最大化||w||−1。这等价于最小化||w||2,于是上式能够重写为:
这就是支持向量机的基本模型。
由于如今的目标函数是二次的。约束条件是线性的。所以它是一个凸二次规划问题。这个问题能够用现成的QP (Quadratic Programming) 优化包进行求解。
一言以蔽之:在一定的约束条件下,目标最优,损失最小。
此外,由于这个问题的特殊结构,还能够通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的长处在于:一者对偶问题往往更easy求解。二者能够自然的引入核函数,进而推广到非线性分类问题。
那什么是拉格朗日对偶性呢?简单来讲,通过给每一个约束条件加上一个拉格朗日乘子(Lagrange multiplier)。定义拉格朗日函数(通过拉格朗日函数将约束条件融合到目标函数里去,从而仅仅用一个函数表达式便能清楚的表达出我们的问题):
然后令
easy验证,当某个约束条件不满足时,比如yi(wTxi+b)<1。那么显然有θ(w)=∞(仅仅要令αi=∞[即i可)。而当全部约束条件都满足时,则最优值为θ(w)=12||w||2,亦即最初要最小化的量。
因此,在要求约束条件得到满足的情况下最小化12||w||2,实际上等价于直接最小化θ(w)(当然,这里也有约束条件。就是αi≥0,i=1,…,n)。由于假设约束条件没有得到满足,θ(w)会等于无穷大,自然不会是我们所要求的最小值。
详细写出来,目标函数变成了:
这里用表示p∗这个问题的最优值,且和最初的问题是等价的。假设直接求解,那么一上来便得面对w和b两个參数,而αi又是不等式约束,这个求解过程不好做。最好还是把最小和最大的位置交换一下,变成:
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用d∗来表示。
并且有d∗≤p∗,在满足某些条件的情况下。这两者相等,这个时候就能够通过求解对偶问题来间接地求解原始问题。
换言之。之所以从minmax的原始问题p∗,转化为maxmin的对偶问题d∗,一者由于d∗是p∗的近似解。二者,转化为对偶问题后。更easy求解。
以下能够先求L 对w、b的极小,再求L 对的极大。
对偶问题求解的3个步骤:
1)、首先固定,要让 L 关于 w 和 b 最小化,我们分别对w,b求偏导数。即令 ∂L/∂w 和 ∂L/∂b 等于零:
将以上结果代入之前的L:
得到:
有读者可能会问上述推导过程怎样而来?说实话,其详细推导过程是比較复杂的。例如以下图所看到的:
最后,得到:
“倒数第4步”推导到“倒数第3步”使用了线性代数的转置运算,由于ai和yi都是实数。因此转置后与自身一样。
“倒数第3步”推导到“倒数第2步”使用了(a+b+c+…)(a+b+c+…)=aa+ab+ac+ba+bb+bc+…的乘法运算法则。最后一步是上一步的顺序调整。
从上面的最后一个式子,我们能够看出,此时的拉格朗日函数仅仅包括了一个变量,那就是αi(求出了αi便能求出w和b)。
2)求对α的极大,即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,仅仅有α。从上面的式子得到:
这样,求出了αi。依据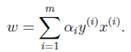
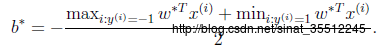
3)在求得L(w, b, a) 关于 w 和 b 最小化。以及对α的极大之后,最后一步则能够利用SMO算法求解对偶问题中的拉格朗日乘子α。
线性支持向量机以及软间隔最大化
假设给定一个特征空间上的训练数据集
T=(x1,y1),(x2,y2),......(xN,yN)
假设训练数据集不是线性可分的。通常情况是。训练数据中有一些特异点,将这些特异点去除以后。剩下的大部分的样本点组成的集合是线性可分的。
线性不可分意味着某些样本点(xi,yi)不能满足函数间隔大于等于1的约束条件,为了解决问题,能够对每一个样本点(xi,yi)引进一个松弛变量ζi≥0。这样,约束条件变为:
yi(wxi+b)≥1−ζi
同一时候。对于每一个松弛变量ζi。支付一个代价ζi,目标函数由原来的
12||w||2变为:
12||w||2+C∑i=1Nζi
这里,C>0称为惩处參数,一般由应用问题决定,C值大时对误分类的惩处增大。
C值小时对误分类的惩处减小。此时。最小化目标函数有两层含义:使12||w||2尽量小,同一时候使误分类的个数尽量少。C是调和二者的系数。
有了上面的思路,上面问题变成例如以下凸二次规划问题(原始优化问题):
上面的对偶问题是:
原始优化问题的拉格朗日函数是:
到眼下为止,我们的 SVM 还比較弱,仅仅能处理线性的情况。以下我们将引入核函数,进而推广到非线性分类问题。
非线性支持向量机和核函数
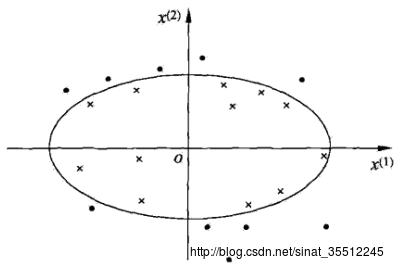
非线性分类问题是指通过利用非线性模型才干非常好地进行分类的问题。先看一个样例:
由上图可见。无法用直线(线性模型)将正负实例正确分开。可是我们却能够用一条椭圆双曲线(非线性模型)将他们正确分开。
非线性问题往往不好求解,我们能够将样本从原始空间映射到一个更高维的特征空间。使得样本在这个特征空间内线性可分。
正如上面的样例。通过将原始的二维空间映射到一个合适的三维空间,就能找到一个合适的超平面。
上面的样例说明,用线性分类方法求解非线性分类问题分为两步:首先使用一个变换将原来的空间的数据映射到新空间;然后在新空间里用线性分类学习方法从训练数据集中学习分类模型。核技巧就是属于这个方案。
令Φ(x)表示将x映射后的特征向量,于是在特征空间中超平面所相应的模型可表示为
f(x)=wTΦ(x)+b
相似地,可得到:
其对偶问题是:
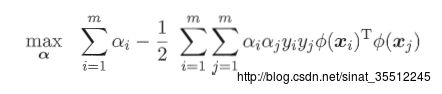
我们注意到上面式子的计算涉及到了就算Φ(xi)TΦ(xj),这是样本xi与xj映射到特征空间后的内积,由于特征空间的维数可能非常高。甚至可能是无穷维。因此直接计算Φ(xi)TΦ(xj)一般是困难的。因此,我们能够设想有这样一个函数:
k(xi,xj)=<Φ(xi),Φ(xj)>=Φ(xi)TΦ(xj)
然后用上面的式子。我们就不必直接去计算高维甚至无穷维特征空间的内积,于是,我们能够将公式改写成例如以下:
求解后,得到
这里的k(xi,xj)就是核函数。
那么经常使用的核函数都有什么呢?
1、线性核是最简单的核函数,核函数的数学公式例如以下:
2、多项式核实一种非标准核函数,它非常适合于正交归一化后的数据,其详细形式例如以下:
这个核函数是比較好用的,就是參数比較多,可是还算稳定。
3、这里说一种经典的鲁棒径向基核。即高斯核函数,鲁棒径向基核对于数据中的噪音有着较好的抗干扰能力。其參数决定了函数作用范围。超过了这个范围,数据的作用就“基本消失”。
高斯核函数是这一族核函数的优秀代表,也是必须尝试的核函数。其数学形式例如以下:
尽管被广泛使用。可是这个核函数的性能对參数十分敏感,以至于有一大把的文献专门对这种核函数展开研究,相同。高斯核函数也有了非常多的变种,如指数核,拉普拉斯核等。
4、指数核函数就是高斯核函数的变种,它仅仅是将向量之间的L2距离调整为L1距离,这样修改会对參数的依赖性减少,可是适用范围相对狭窄。其数学形式例如以下:
5、拉普拉斯核全然等价于指数核,唯一的差别在于前者对參数的敏感性减少。也是一种径向基核函数。
6、Sigmoid 核来源于神经网络,如今已经大量应用于深度学习,是当今机器学习的宠儿,它是S型的,所以被用作于“激活函数”。关于这个函数的性质能够说好几篇文献,大家能够随便找一篇深度学习的文章看看。
7、 二次有理核完全然全是作为高斯核的替代品出现。假设你认为高斯核函数非常耗时,那么最好还是尝试一下这个核函数,顺便说一下,这个核函数作用域虽广,可是对參数十分敏感,慎用!
。。。
此外,还可通过函数组合得到,比如:
1.若k1和k2为核函数。则对于随意正数a和b,其线性组合
ak1(x,z)+bk2(x,z)
也是核函数;
2.若k1和k2为核函数,则核函数的直积
k1⨂k2(x,z)=k1(x,z)k2(x,z)
也是核函数。
3.若k1为核函数。则对于随意函数g(x),
k(x,z)=g(x)k1(x,z)g(z)
也是核函数;
核函数的选择
至于究竟该採用哪种核,要依据详细问题,有的数据是线性可分的,有的不可分。须要多尝试不同核不同參数。假设特征的提取的好,包括的信息量足够大,非常多问题都是线性可分的。当然,假设有足够的时间去寻找RBF核參数,应该能达到更好的效果。
參考资料:
1、支持向量机通俗导论(理解SVM的三层境地)
2、李航 - <<统计学习方法>>
3、周志华 - <<机器学习>>
相关博客:
1、机器学习系列之机器学习之决策树(Decision Tree)及其Python代码实现
2、机器学习系列之机器学习之Validation(验证,模型选择)
3、机器学习系列之机器学习之Logistic回归(逻辑蒂斯回归)
4、机器学习系列之机器学习之拉格朗日乘数法
本文链接:https://my.lmcjl.com/post/7957.html


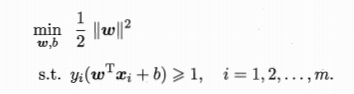
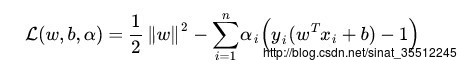
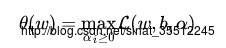
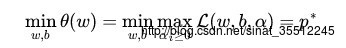
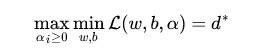
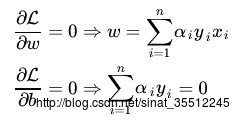
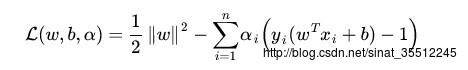
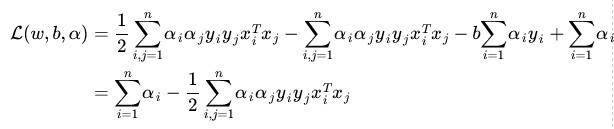
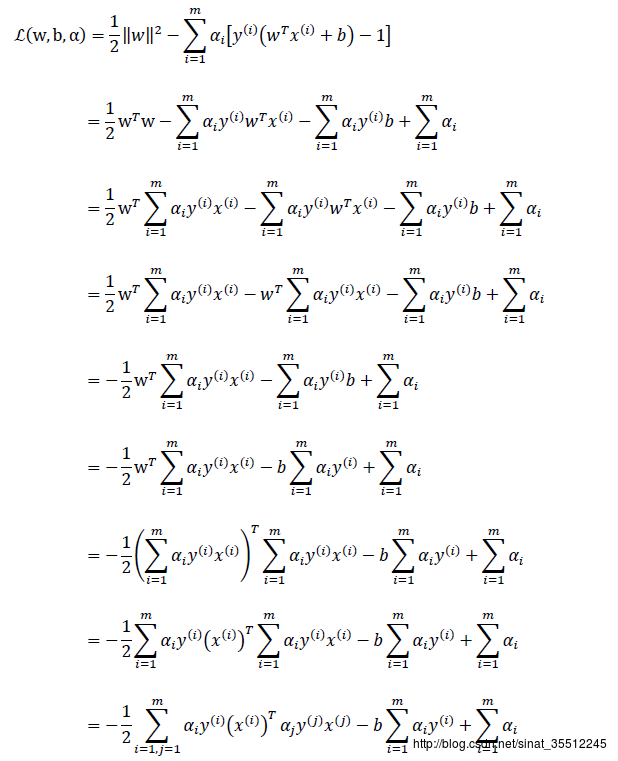
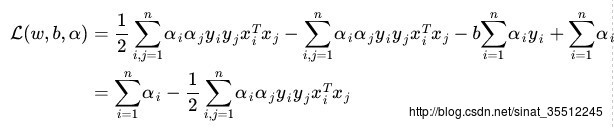
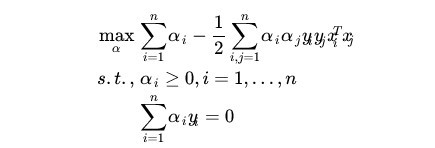
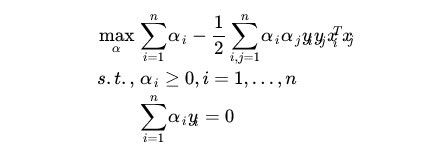
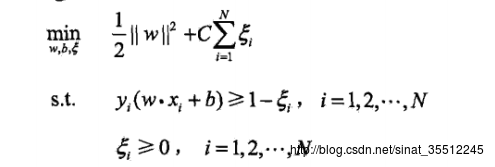
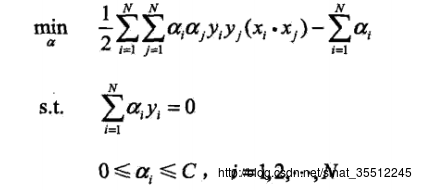
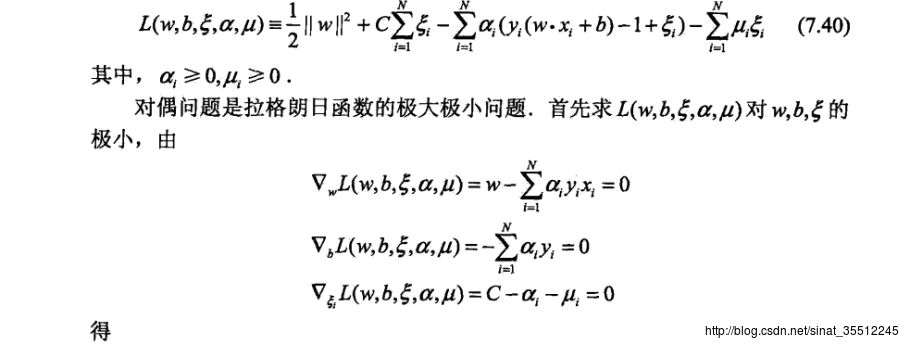
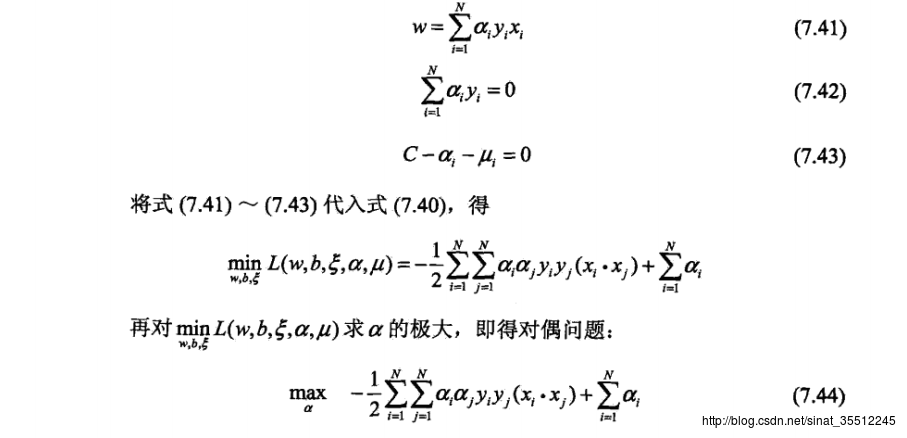


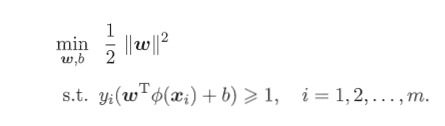
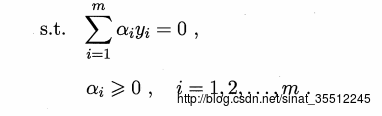
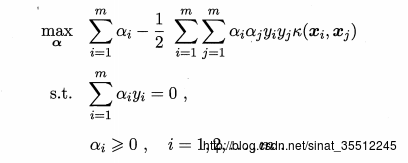
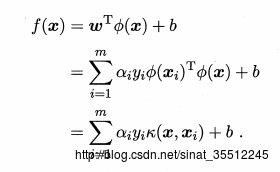
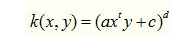
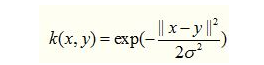
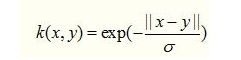
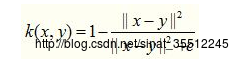
4 评论