目录 ✿LeetCode102.二叉树的层序遍历❀  ✿LeetCode226.翻转二叉树❀  ✿LeetCode101.对称二叉树❀ ✿LeetCode102.二叉树的层序遍历❀ 链接：102.二叉树的层序遍历   public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> result=new ArrayL 继续阅读

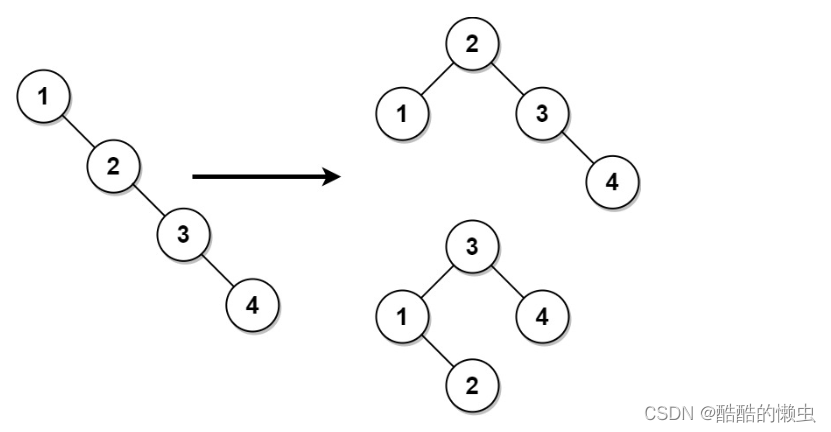
❓1382. 将二叉搜索树变平衡 难度：中等 给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。 如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。 示例 1： 示例 2： 提示： 树节点的数目在 [ 1 , 继续阅读

题目链接 题目描述 给你一棵二叉树的根节点 root，翻转这棵二叉树，并返回其根节点。 示例 1： 示例 2： 示例 3： 提示： 树中节点数目范围在 [0,100][0, 100][0,100] 内−100<=Node.val<=100-100 <= Node.val <= 100−100<=Node.v 继续阅读

目录 ✿二叉树的递归遍历❀ ☞LeetCode144.前序遍历 ☞LeetCode145.二叉树的后序遍历  ☞LeetCode94.二叉树的中序遍历  ✿二叉树的迭代遍历❀  ☞LeetCode144.前序遍历  ☞LeetCode145.二叉树的后序遍历   ☞LeetCode94.二叉树的中序遍历  ✿二叉树的统一迭代遍历❀   ☞LeetCode144.前序遍历  ☞LeetCode145.二叉树的后序遍历  ☞LeetCode94.二叉树的中序遍历   继续阅读

❓ 116. 填充每个节点的下一个右侧节点指针 难度：中等 给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下： struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。 初始状 继续阅读

如果需要查找的值比节点小，会向左子树方向查找，如果比节点值大，会向右子树方向查找     拓展为5叉的形态 5叉排序树的定义  num是这个节点中真实存在的节点个数 那么一个节点中 最少有1个关键字，两个分叉 最多有4个关键字，五个分叉 结点内的关键词有序 失败节点范围  试图查找    比根结点小， 比5大，比11小，在 继续阅读

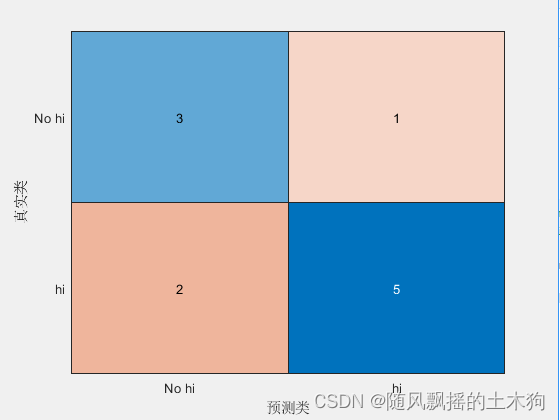
【MATLAB第42期】基于MATLAB的贝叶斯优化决策树分类算法与网格搜索、随机搜索对比，含对机器学习模型的评估度量介绍 网格搜索、随机搜索和贝叶斯优化是寻找机器学习模型参数最佳组合、交叉验证每个参数并确定哪一个参数具有最佳性能的常用方法。 一、 评估指标 1、分类 1.1 准确性 1.2 精度 1.3 召回 1.4 F1值 1.5 F0.5值 1.6 F2值 1.7 计算评估指标的功能 2、回归 2.1 平均绝对误差 2.2 均方误差 2.3 均方根误差 二、 基于F1值执 继续阅读

编程测试 1. 我想用golang实现二叉树前序，请你帮我写一下代码。 // 定义二叉树节点 type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode }// 前序遍历 func PreOrderTraversal(root *TreeNode) {if root == nil {return}fmt.Println(root.Val)PreOrderTraversal(root.Left)Pr 继续阅读

快速生成树协议（spanning-tree） 一、简介1.1 协议版本1.2 技术原理1.3 快速生成树有点 二、CLI命令2.1 信息查看2.2 快速生成树创建 三、具体实现1. SWRoot2. SWLeaf3. SWLeafRight 一、简介 1.1 协议版本 STP、RSTP（快速生成树协议）MSTP（多生成树协议）其中STP一般默认启用，通过两台交换机之间传送BPD 继续阅读

一、生成树 二、802.1D，标准生成树: 1、BPDU:网桥协议数据单元 分为配置BPDU--config-BPDU(用于生成树的选举以及重收敛)和拓扑变更--TC-BPDU(通知交换网络出现了拓扑变更)。 2、数据结构 STP按照如下顺序选择最优的配置BPDU: 在这四条原则中（每条原则都对应配置BPDU中的相应字段），第一条原则主要用于在网络中选举根桥，后面的原则主要用于选举根接口及指定接口。 继续阅读

专注 效率 记忆 预习 笔记 复习 做题 本题出自 acwing网站 这个系列是免费的 打卡即刻退回费用。 第三天【剑指Offer例题代码 系列】 6. 重建二叉树根据前序遍历和中序遍历 得到树 补充题：树的遍历 7. 二叉树的下一个节点 6. 重建二叉树 原题链接 根据前序遍历和中序遍历 得到树 过程如下： 首先根据前序遍历找到 根节点找到中序遍历中，该根节点的位置中序中 位于 根节点左边的就是 左子树&#xf 继续阅读

生成树协议（Spanning Tree Protocol，STP） STP 为什么需要生成树 冗余/备份是必须的，环路不可避免 环路危害 广播风暴 MAC地址学习错误/震荡/漂移 无法通信/重复数据帧接收 什么是生成树STP 在二层网路中，有选择性地阻塞环路中的某个接口来消除二层环路，·形成树状拓扑，避免了环路，同时还具备链路备份的功能， 当活动链路发生故障时&#xff0 继续阅读