本文将从多个方面介绍线性估算计算公式，包括定义、公式推导、代码示例、应用场景等。 一、定义 线性估算是指在一组数据中寻找一种线性关系，使得该关系能够最好地描述这组数据。估算的目的是为了预测未来的趋势或值。 简单地说，线性估算就是要通过已有的数据来推算出未来可能会出现的数据。 二、公式推导 线性估算的核心公式是y = ax + b，其中y表示预测值，x表示自变量，a和b分别表示斜率和截距，也称为回归系数。 斜率的计算公式为a = cov(x,y) / var(x 继续阅读

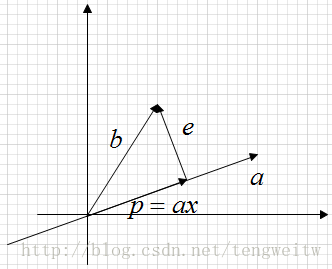
我们在初中就应该学过投影，那么什么是投影呢？形象点说，就是将你需要投影的东西上的每一点向你要投影的平面作垂线，垂线与平面的交点的集合就是你的投影。注意这里我们的投影是向量的投影，几何的投影(并不一定是垂直投影的)可见度娘百科。同样的，我们从简单的二维投影来开始讨论。    1、二维投影 上图表示的是，向量b在向量a上的投影。显然有如下表达式： 其中，P 继续阅读

1.写出用傅立叶数值法求解非线性偏微分方程中的波方程(wave equation)的Python代码 傅立叶数值法是一种求解偏微分方程的方法，它利用傅立叶变换将偏微分方程从时域转换到频域，然后求解频域中的方程，最后利用逆傅立叶变换得到时域中的解。 以下是一个使用傅立叶数值法求解一维非线性波动方程的Python代码示例。这里我们考虑一个简单的非线性项（u^2），你可以根据需要调整非线性项。 import nu 继续阅读

本文将从数据拟合的理论和应用角度出发，介绍二次函数数据拟合模型的相关知识和实际案例，并给出完整的代码示例，帮助读者更好地掌握二次函数拟合的方法和技巧。 一、基本概念 在数据分析和建模中，经常会遇到需要拟合一个函数曲线到已有数据点的情况。而二次函数是一种常见的、能够较好地拟合一些非线性数据的函数形式。 二次函数一般的形式为：$y=ax^2+bx+c$，其中 $a$、$b$、$c$ 分别是二次函数的系数，$x$ 为自变量，$y$ 为因变量。在二次函数中，$a$ 的 继续阅读

加权最小二乘法（weighted least squares，简称WLS）是一种用于线性回归的方法，与普通最小二乘法相比，可以更好地处理误差方差不同的情况。接下来将从定义、优点、应用、示例等多个方面对加权最小二乘法python进行详细阐述。 一、定义 加权最小二乘法是一种用于处理误差方差不同的情况的线性回归方法。在加权最小二乘法中，误差较小的数据点给予更大的权重，误差较大的数据点给予更小的权重。这种方法可以更好地拟合真实数据，并且可以有效地提升模型的准确度。 继续阅读

基本思想 基数排序(radixsort)是在桶排序的基础上发展而来的，两种排序都是分配排序的高级实现。分配排序(distributivesort)的基本思想：排序过程无须比较关键字，而是通过“分配”和“收集”过程来实现排序。它们的时间复杂度可达到线性阶：o(n)。 基数排序是一种稳定的排序算法，但有一定的局限性： 　　1、关键字可分解。 　　2、记录的关键字位数较少，如果密集更好 　　3、如果是数 继续阅读

前言 栈是什么，你可以理解为一种先入后出的数据结构（First In Last Out），一种操作受限的线性表... C实现 借助与C语言中的void指针及函数指针，我们可以实现一个链式通用栈： ? 1 2 3 继续阅读

文章目录 2.1 对偶规划2.1.1 问题的提出2.1.2 对偶规划的定义 49年Abr.W.Tucker Princeton的Harold W.kuhn布朗大学的David GaleLP都有个影像,称LP对偶规划 它是LP的一个有趣的性质 对称、影子、映射问题 原来的LP称原始问题 其对称问题为对偶问题 原始与对偶问题 是同一问题反映出来的两侧面 2.1 对偶规划 线性规划问题都对应一个对偶线性规划问题 二者从不同的角度描述相同问题根据同样条件和数据建立不同数学模型 继续阅读

1: 3DMAX中我想制作白色的或者彩色的黑板材质,如何使找到的贴图的黑板的... 1、使用max的混合材质来呈现黑色条和白色条的效果。 2、在贴图中加入遮罩的条，将上面的贴图放在遮罩中，可以使用ps预处理贴图。 2: 下载的3Dmax模型导入后全是黑色的,也装了vray。而且为了看看是否能用... 1、修改线性渲染器 2、要求上传渲染后的图片 3、询问下载的模型格式是否为3ds格式 3: 3DMAS和CAD有什么区别 1、计算机辅助设计( 继续阅读

我们经常会发现，历时四年软件专业的大学生毕业居然找不到工作，即便找到了工作也只能是做一些简单的辅助性工作。 那么我们不禁要问，究竟是什么原因让我们可爱的大学生们学而无用，或者用而不学呢？ 我认为主要是因为现在的科学技术进步太快了，互联网技术出现以后人类的技术开始了指数级增长，正是因为这种增长，让线性增长的传统学校教育跟不上社会的发展。 从教育的发展历史来看， 继续阅读

一、CRC编码简介 CRC 的英文全称为 Cyclic Redundancy Check（Code），中文名称为循环冗余校验（码）。它是一类重要的线性分组码，编码和解码方法简单，检错和纠错能力强，在通信领域广泛地用于实现差错控制。 二、CRC编码过程 以下步骤将描述 6 字节红外控制码生成过程： 1．从二维码的中依次顺序提取前 2 个英文字母、最后 继续阅读

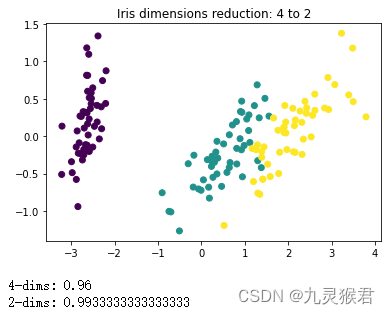
基于PCA与LDA的数据降维实践 描述 数据降维（Dimension Reduction）是降低数据冗余、消除噪音数据的干扰、提取有效特征、提升模型的效率和准确性的有效途径， PCA（主成分分析）和LDA（线性判别分析）是机器学习和数据分析中两种常用的经典降维算法。 本任务通过两个降维案例熟悉PCA和LDA降维的原理、区别及调用方法。 源码下载 环境 操作系统：Windo 继续阅读