在Python编程中，我们常常需要对矩阵进行操作。而获取矩阵的某一列是一个常见需求，本文将介绍如何使用Python获取矩阵的某一列，并从以下几个方面进行详细阐述： 一、numpy库的方法 numpy是Python中一个常用的数学库，其中包含了许多操作矩阵的方法。我们可以使用其中的slice方法来获取矩阵的某一列。 import numpy as np # 创建一个5行3列的矩阵 matrix = np.array([[1, 2, 3], 继续阅读

1.在Qgis里面的设置里面新建一个Albers投影，KWT信息参考：https://blog.csdn.net/QGISClass/article/details/112344243 2.在画图的时候，主要属性的“坐标参考系（CRS）”需要改成Albers 3.在新建网格的时候，网格的“坐标参考系（CRS）”需要改成WGS84 继续阅读

TypeScript (简称ts) 是一种静态类型的编程语言，在类型检查和类型推导方面具有一定的优势。类型推导是TypeScript在代码编写的过程中自动识别并设置变量类型，从而提高代码的可读性和健壮性，减少了代码中潜在的错误。 在 TypeScript 中，类型推导是一种根据代码语法分析变量类型的机制。如果代码中指定了变量的类型，则 TypeScript 会使用该类型，否则 TypeScript 会根据上下文 继续阅读

def matrixMultiply(A, B):# 获取A的行数和列数A_row, A_col = shape(A)# 获取B的行数和列数B_row, B_col = shape(B)# 不能运算情况的判断if(A_col != B_row):raise ValueError# 最终的矩阵result = []# zip 解包后是转置后的元组，强转成list, 存入result中BT = [list(row) for row in zip( 继续阅读

Python是一种高级语言，用于Web开发，人工智能和机器学习等。它有着简单易学的语法以及丰富的开源库，使得开发者能够快速地完成任务。在本篇文章中，我们将探讨如何使用Python生成对角线为1的矩阵。 一、基础概念 在开始生成对角线为1的矩阵之前，我们需要了解一些基本概念。 矩阵是一个由固定数量的行和列组成的矩形数组。使用Python，我们可以使用列表（list）来表示矩阵。一个矩阵可以通过以下方式表示： matrix = [ [1, 0, 0], 继续阅读

在计算机科学中，矩阵是一种非常重要的数据类型，它被广泛用于科学计算、图形学、机器学习等领域。在程序中，将一个数组转换为矩阵是必备的基本技能之一。 一、将一维数组转换为二维矩阵 在程序中，通常使用一维数组来表示矩阵。将一维数组转换为二维矩阵的方法如下： int[] arr = new int[]{1, 2, 3, 4, 5, 6}; int row = 2; int column = 3; int[][] matrix = new int[row][colum 继续阅读

用numpy的库，没有去下。 创建矩阵 from numpy import *; a1=array([1,2,3]); a1=mat(a1);data1=mat(zeros((3,3))); #创建一个3*3的零矩阵，矩阵这里zeros函数的参数是一个tuple类型(3,3) data2=mat(ones((2,4))); #创建一个2*4的1矩阵，默认是浮点型的数据，如果需要时int类型&#xff0c 继续阅读

问题描述 在  n x n  的网格  grid  中，我们放置了一些与 x，y，z 三轴对齐的  1 x 1 x 1  立方体。 每个值  v = grid[i][j]  表示  v  个正方体叠放在单元格  (i, j)  上。 现在，我们查看这些立方体在  xy 、yz  和  zx  平面上的投影。 投影  就像影子，将  三维  形体映射到一个  二维  平面上。从顶部、前面和侧面看立方体时&#x 继续阅读

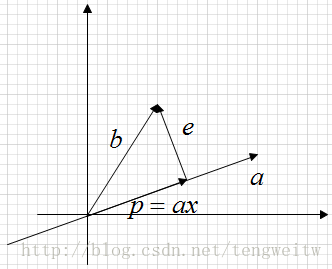
我们在初中就应该学过投影，那么什么是投影呢？形象点说，就是将你需要投影的东西上的每一点向你要投影的平面作垂线，垂线与平面的交点的集合就是你的投影。注意这里我们的投影是向量的投影，几何的投影(并不一定是垂直投影的)可见度娘百科。同样的，我们从简单的二维投影来开始讨论。    1、二维投影 上图表示的是，向量b在向量a上的投影。显然有如下表达式： 其中，P 继续阅读

用for循环实现的卷积层： 卷积运算： import time """ 定义2维度卷积的非矩阵操作""" def Conv2d(X,W, stride, pad, dilation=1):"""参数说明：:param X: 输入，batchsize, in_rows, in_cols, in_channels.:param W: 权重&#xff0 继续阅读

基于得分[Score-Based]的随机微分方程生成建模 1. 梗概 该框架封装了基于得分的生成建模和扩散概率建模，产生新的采样过程和新的建模能力。 在求解反向时间SDE中， 我们引入了一个预测-校正框架来校正离散化反向时间SDE演化中的误差。我们还推导出了一个等效的神经ODE，它从与SDE相同的分布中进行采样，但还可以进行精确的似然计算，并提高采样效率。我们还提供了一种使用基于得分的模型解决反向问题的新方法，正如类条件生成、图像修复和彩色化的实验所证明的那样。 结合 继续阅读

ChatGPT能否取代Google、百度这样的传统搜索引擎？为什么中国不能很快做出ChatGPT？当前，对这些问题的探讨大多囿于大型语言模型（LLM）的技术可行性，忽略或者非常粗糙地估计了实现这些目标背后的经济成本，从而造成对LLM的开发和应用偏离实际的误判。 本文作者从经济学切入，详细推导了类ChatGPT模型搜索的成本、训练GPT-3以及绘制LLM成本轨迹的通用框架&#xff0 继续阅读