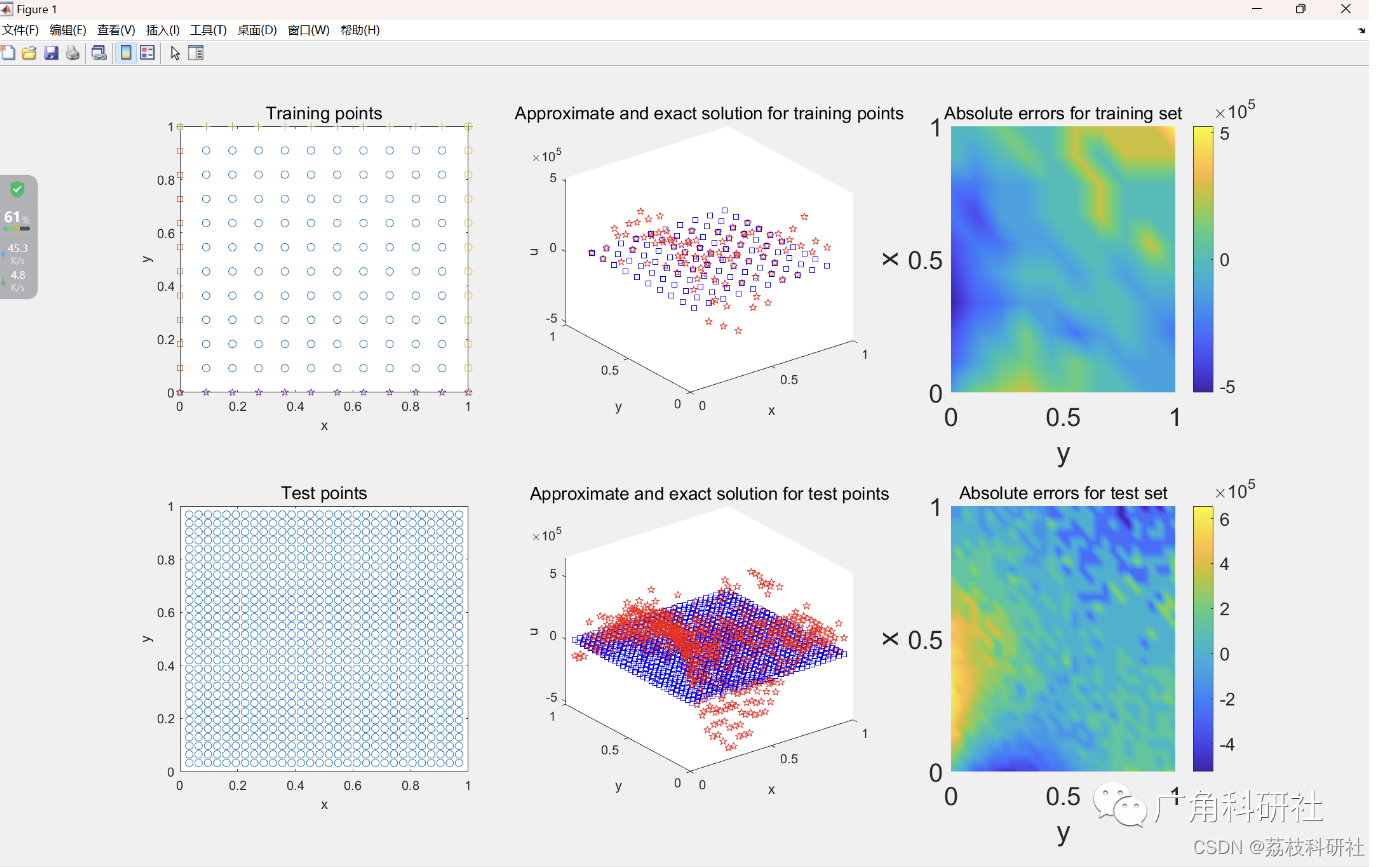
💥1 概述 本代码说明了“最小二乘支持向量机”在学习偏微分方程 （PDE） 解方面的应用。提供了一个示例，并将获得的结果与精确的解决方案进行比较。 📚2 运行结果 部分代码： clc; clear all; close all warning('off','all') a0=0; b0=1; n=11; h=( 继续阅读

基于得分[Score-Based]的随机微分方程生成建模 1. 梗概 该框架封装了基于得分的生成建模和扩散概率建模，产生新的采样过程和新的建模能力。 在求解反向时间SDE中， 我们引入了一个预测-校正框架来校正离散化反向时间SDE演化中的误差。我们还推导出了一个等效的神经ODE，它从与SDE相同的分布中进行采样，但还可以进行精确的似然计算，并提高采样效率。我们还提供了一种使用基于得分的模型解决反向问题的新方法，正如类条件生成、图像修复和彩色化的实验所证明的那样。 结合 继续阅读

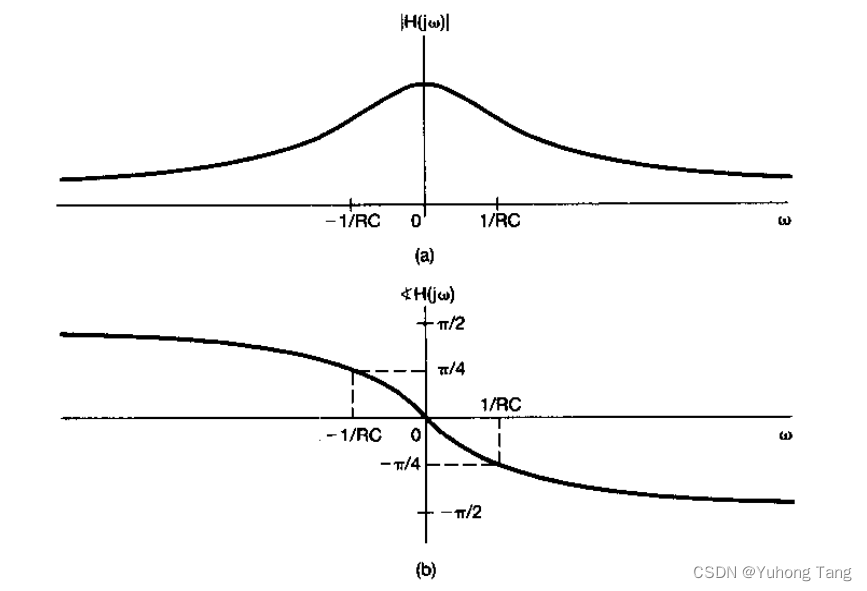
用微分方程描述的连续时间滤波器举例   在许多应用中，频率选择性滤波器是用线性常系数微分或差分方程描述的线性时不变系统来实现的。这有许多理由，例如很多具有滤波作用的物理系统都是由微分或差分方程表征的。这方面的一个很好的例子就是在后续将研究的汽车减震系统，在某种程度上这个系统的设计就是为了滤掉由道路表面不平坦引起的高频颠簸和起伏。利用由微分或差分方程描述的滤波器的第二个原因是，它们能很方便地用模拟硬件或数字硬件来实现。另外，由 继续阅读

本文主要介绍如何利用函数图象求解方程，下面从多个方面进行详细阐述。 一、基本概念 在解方程时，我们通常会用到函数图象。函数图象是将一个函数的自变量与因变量之间的关系用图像表示出来，因而也叫做函数的图形或者曲线。 函数图象的表示方法是将自变量和函数值分别作为坐标轴上的横纵坐标，然后用线条或者曲线将坐标点连接起来，形成一个图形。 二、使用函数图象求解一元一次方程 对于形如 $ax+b=0$ 的一元一次方程，我们可以将其变形成 $y=ax+b$ 的函数形式，然后将该 继续阅读

Python有不少求根的办法，但是都是求一重根的，不太适用。 在这个问题上用的是暴力搜索法：记 $$F(x)=f(x)-y$$ 判断每个 x 对应的 $F(x)$ 的符号，如果$F(x_i)<0,\ F(x_{i+1})>0$，或者$F(x_i)>0,\ F(x_{i+1})<0$，则取该$F(x)=0$的根为$$x_0=(x_i+x_{ 继续阅读

1.写出用傅立叶数值法求解非线性偏微分方程中的波方程(wave equation)的Python代码 傅立叶数值法是一种求解偏微分方程的方法，它利用傅立叶变换将偏微分方程从时域转换到频域，然后求解频域中的方程，最后利用逆傅立叶变换得到时域中的解。 以下是一个使用傅立叶数值法求解一维非线性波动方程的Python代码示例。这里我们考虑一个简单的非线性项（u^2），你可以根据需要调整非线性项。 import nu 继续阅读

引言 众所周知的是，在大学课程中一般只会教授一种拟合方法(也即参数估计方法)——最小二乘法。这是一种直接求解的方法，非常的有效，不仅是损失最小解，而且是最大似然解。只不过，有一个缺点，它只能解决线性方程参数问题，对于非线性曲线，就无能为力了。大部分情况下还是将其转换成线性问题，再使用最小二乘法。 然而，并非所有的问题都能转换为线性问题，甚至 继续阅读

一、ChatGPT简介    ChatGPT 是 OpenAI 开发的人工智能聊天机器人。该聊天机器人基于 GPT-3.5 语言模型，经过训练可以对用户给出的指令做出详细响应。与其他聊天机器人不同，ChatGPT 可以回答后续问题、求解数学方程式、撰写文本、修复和调试代码以及总结文本。它还可以在语言之间进行翻译。   ChatGPT 基本上是为聊天机器人应用程序设计的 GPT-3 模型的变体。 该公司通过使用大量对话文本数据对其进行了训练。 因此，它可 继续阅读

今天正好有点时间就想着把之前零星时间里面做的一点小东西整合一下梳理出来，本文的核心目的就是想要基于python来开发实现各种有趣的数学曲线的可视化展示。 笛卡尔心形线 笛卡尔心形线是一种二维平面曲线，由法国数学家笛卡尔在17世纪提出。它得名于其形状类似于传统的心形符号 ❤️。 笛卡尔心形线的方程可以表示为： (x^2 + y^2 - 1)^3 - x^2 * y^3 = 0 其中，(x, y) 是心形线上的点坐标。 继续阅读

里查德米尔RICHARD MILLE是世界顶级腕表品牌之一，该品牌创立于2001年，简称“RM”。它以革命性的制表技术，研制出最精密的陀飞轮腕表驰名于世。“我的目标是要制作出手表业界的‘一级方程式’。 里查德米尔手表保养方法 1、手表不得遭受严重撞击或跌摔，请勿将手表强力碰触硬度相同或更高的物品表面,如氧化金属、石英水晶、磨石、砂纸、花岗岩面、混凝土墙面等。手表摘下时养成习惯将其放在安全位置。 2、请定期清洁表带、表壳。建议到专业手表清洁 继续阅读

一阶数字低通滤波器传递函数为： ωc=2πfc ωc​为滤波截止角频率  :截止频率，单位： HZ 对低通滤波器进行离散化 一  后向差分法 变换公式为： s=(1−z−1)/Ts​ Ts：采样频率 将变化公式带入传递函数，可得差分方程： y(n)=(ωc​Ts​)/(1+ωc​Ts​)x(n)+1/(1+ωc​Ts​) 继续阅读

MATLAB计算平抛阻尼运动 小球在空气中平抛运动的轨迹 [问题]一小球在空气中作平抛运动，初速度为v0，所受的阻力与速率成正比：f = -kv，k称为阻力系数。画出小球运动的轨迹。 [数学模型] 如B7.1图所示，小球受到重力mg，方向向下；空气阻力f，方向与速度方向相反。根据牛顿第二定律可列出直角坐标方程 d2xdxd2ydy，m2 mg k。 (7.1.1) m2 kdtdtdtdt 由于vx = dx/dt，vy = dy/dt，上式可化为 B7.1图 dvdvxkk vx，y g v 继续阅读