带你来看看mybatis为什么报"Invalid value for getInt()"这个错误 背景 使用mybatis遇到一个非常奇葩的问题,错误如下: 场景 还原一下当时的情况: public interface UserMapper { @Results(value = { @Result(property = "id", column 继续阅读
Search Results for: 问题
查询到最新的12条
AutoCAD 2013安装问题汇总及配置要求
1: AutoCAD 2013 这个为什么说什么32位什么的,然后64位的安装不了啊... 1、确认系统是32位还是64位,选择对应的AutoCAD2013安装程序。 2、右键点击计算机,选择属性,查看系统的位数。 3、根据系统位数下载相应的安装包。 4、使用正确的安装程序进行安装。 5、如果遇到问题,提供更详细的信息,如电脑配置、操作系统、安装过程中的错误提示等。 通过以上步骤,能够正确安装并使用AutoCAD2013。 AutoCAD 2013的安装 继续阅读
关于网站新增备案遇到的问题
这段时间在新增备案,经我备案的网站数量已经不知道有多少个了,但是每次多多少少都会遇到一些问题,并且每次遇到的问题基本上都是服务商通过了,但到了管局采驳回。 正常情况下,服务商通过备案审核之后,大概率管局都是直接审核通过的,有一些特殊情况可能会遇到服务商通过,但是管局驳回的情况,这里给大家罗列几点。 个人备案 1.不同主体用了相同的邮箱和手机号 这是之前遇到管局驳回的情况,因为手上的主体比较多,有时候忘记了那一个主体用的哪个邮箱,有时候就用 继续阅读
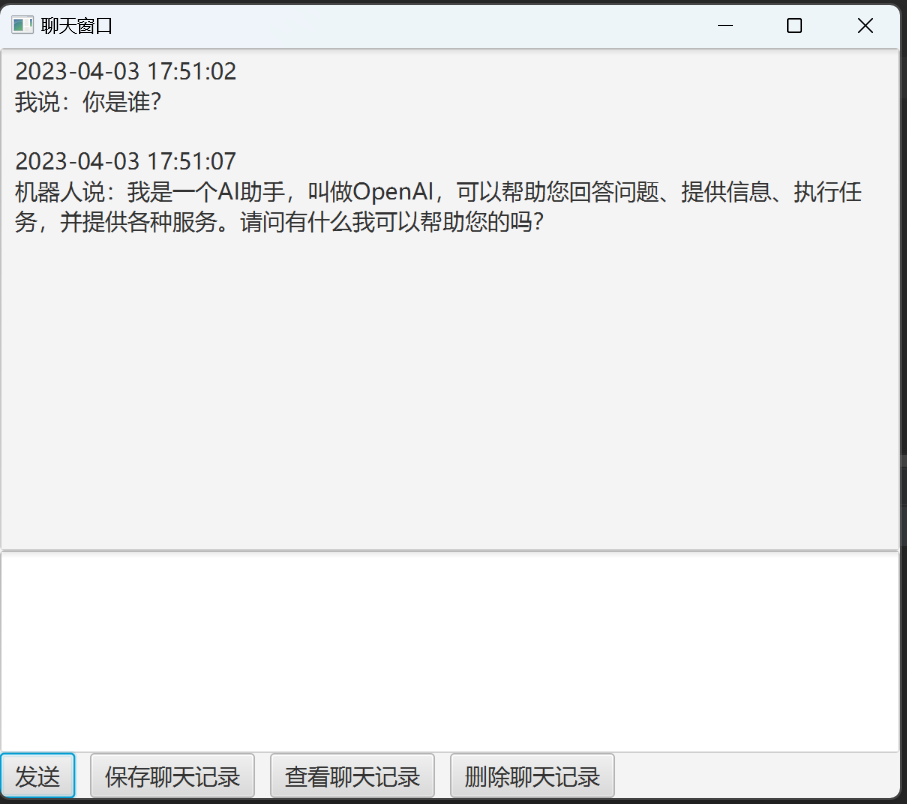
基于ChatGPT API的PC端软件开发过程遇到的问题的分析
一、基于ChatGPT API的PC端软件开发过程遇到的问题的分析 首先来看一下效果图吧! 本客户端使用的是 JavaFX 开发的。JavaFX 相比于 Swing 来说,JavaFX 支持 CSS 样式,如果使用 Java 来开发 GUI 软件的话,还是推荐使用 JavaFX 的。JavaFX 是 2008 年由 Oracle 公司推出的项目。需要说明的是在高版本的 JDK 中不含有 JavaFX 相关的 APIÿ 继续阅读
如何解决Windows软件路由双线切换和电脑双线接入问题?
1: 提问:windows平台的软件路由双线切换问题1、通过计算机管理工具查看网络适配器的信息,获取内网网卡和外网网卡的PCI编号。2、创建两个批处理文件,用于内外网切换。先禁用相应的网卡,然后启用对应的网卡。3、使用DevCon.exe工具进行网卡操作。4、可以使用DevCon.exe命令查看帮助、查看所有PCI网卡的ID、禁用指定的网卡以及启用指定的网卡。5、注意,禁用和启用的网卡ID需要从第一个字符到&字符。2: 电脑怎么接双线1、双线入网并不等于 继续阅读
旅行商问题的动态规划解决
旅行商问题是一个著名的NP问题,不能找到多项式解。不过可以用动态规划的方法把时间复杂度从O(N!)降低到O (2^N)。对于解决小规模的旅行商还是可以实现的。 http://icpc.ahu.edu.cn/OJ/Problem.aspx?id=420 发现枚举过程中还是有很多重复计算的,所以可以存贮一下状态,避免了重复计算。 开辟N+1维数组,dp[N][2][2]..[2] dp[cur] 继续阅读
关于项目转化率的问题,提升项目转化率的方法技巧
突然想起来一个事,就是项目转化率的问题。 咱们不管是做什么样的项目,都会存在一个转化率,老手会琢磨这个转化率,新手只会抱怨来了流量但没转化。 展天会员课程里面说过一个数据,我录制视频的时候,咱们的项目转化率可以做到80%以上,可能很多人理解不了,这是多么恐怖的一个转化率。 这么说吧,很多项目,转化率是0.x%-5%,这是很多行业普遍的一个转化,如果能做到10-15%的转化率,那么都可以拿出来吹嘘很久很久,所以80%的转化,可谓是神一样的存 继续阅读
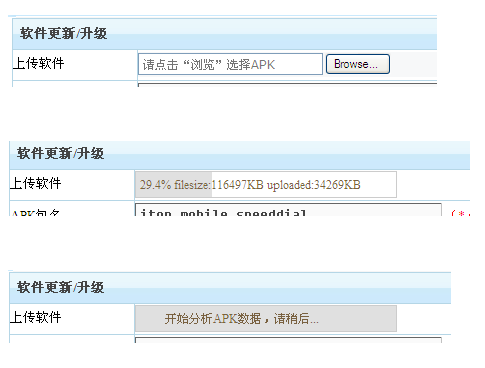
使用php+apc实现上传进度条且在IE7下不显示的问题解决方法
今天整理以前写过的关于上传文件,并显示进度条的程序代码,对该代码进行优化整理。解决了一直困扰的问题:有时进度条没有达到100%,浏览器出现假死现象。在IE8、chrome测试非常完美。 项目需求: 上传APK,显示上传进度条,上传完成开始分析APK,并显示:正在分析apk数据,请稍后... ,分析完成后,显示:上传成功,重新上传 由于我电脑装的是winxp英文版,IE默认的是IE7,在测试的时候发现进度条不显示。百分比也不显示。 排除问题: 继续阅读
Python基于Floyd算法求解最短路径距离问题实例详解
本文实例讲述了Python基于Floyd算法求解最短路径距离问题。分享给大家供大家参考,具体如下: Floyd算法和Dijkstra算法,相信大家都不陌生,在最短路径距离的求解中应该算得上是最为基础和经典的两个算法了,今天就用一点时间来重新实现一下,因为本科的时候学习数据结构才开始接触的这个算法,当时唯一会用的就是C语言了,现在的话,C语言几乎已经离我远去了,个人感觉入手机器学习以来python更得我心,因为太通俗易懂了,带给你的体验自然也是非常不错的。 当然网 继续阅读
01 背包问题解析与代码 python 实现
01 背包问题解析与代码 问题定义 给定一堆具有不同重量 { w 1 , w 2 , ⋯ , w n } \{ w_1,w_2, \cdots,w_n \} {w1,w2,⋯,wn}与价值 { v 1 , v 2 , ⋯ , v n } \{ v_1,v_2, \cdots,v_n \} {v1,v2,⋯,vn}的背包(knapsack),在总重量为 W 的情况下,如何选取背包才能获得最大价值?其中 继续阅读
力扣算法刷题Day44|动态规划:完全背包问题 零钱兑换II 组合总和Ⅳ
力扣题目:#518.零钱兑换II(完全背包组合问题) 刷题时长:7min 解题方法:动态规划(完全背包) 复杂度分析 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度空间复杂度: O(m) 问题总结 对递推公式的理解 本题收获 题意转换:纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物 继续阅读
Nginx解决前端访问资源跨域问题的方法详解
被前端跨域问题折磨快2天后,终于用ngnx的方式解决了,所以在此总结下。 该篇只探讨如何用Ngnx解决跨域问题,对于原理不作讨论。 1、首先介绍Windows环境下Nignx的相关命令操作 nginx常用命令: 验证配置是否正确: nginx -t 查看Nginx的版本号:nginx -V 启动Nginx:start nginx 快速停止或关闭Nginx:nginx -s stop 正常停 继续阅读