1.BitSet介绍

BitSet是用于存储二进制位和对二进制进行操作的Java数据结构，BitSet从jdk1.0开始就有了。它存储的是二进制位在BitSet中状态，根据对这些状态的判断，可以有很多应用。以前对数据的操作都是先把数据都是存储在内存中间的，现在可以通过设置BitSet的相应位达到存储数据信息的目的，极大的节省了内存空间。

2.BitSet应用

BitSet可以做的事情主要分为以下几类：

（1）大数据量的查找。

（2）大数据量的去重。

（3）大数据量的统计。

（4）大数据量的排序。

（5）求数据的并集、交集、补集等。

（6）大数据量的判别。

BitSet常见的应用是那些对海量数据进行一些统计工作，比如日志分析、用户数统计等等。

BitSet能够做以上事情主要依靠BitSet的基本操作，对应的常用方法：

（1）初始化一个BitSet。使用构造函数BitSet( )或BitSet(int nbits)。

（2）设置BitSet的某一指定位。就是把指定位存放入BitSet，使用设置函数set(int bitIndex)。

（3）获取BitSet的某一位的状态。就是判断指定位是否在BitSet中，boolean型的返回值，使用函数get(int bitIndex)。

（4）清空BitSet或清空BitSet的某一指定位。就是把BitSet所有位或指定位清除，使用清空函数clear( )或clear(int bitIndex)。

不过使用BitSet有一点需要注意：在没有外部同步的情况下，多个线程操作一个BitSet是不安全的。所以在多线程环境下使用BitSet要考虑线程安全的问题，可以使用多线程安全策略确保多个线程在执行过程中的的线程安全性。也就是BitSet是非线程安全的，需要外部同步。

2.BitSet应用举例

下面就来看一个BitSet应用的具体例子。

（1）使用BitSet查找电话号码

从一堆数量大概在千万级的电话号码列表中找出所有重复的电话号码，需要时间复杂度尽可能小。

如果这个问题使用暴力搜索时间复杂度太高，就不考虑这种解决方案。

容易想到的办法就是建立一个标志数组，int boolean都行，用相应的位置值来代替这个号码是否出现，根据数组的可直接存取特性，来提高效率。比如电话号“8832061”如果存在，就把他放入数组的第8832061位设置该位的值为1或true。

但是这样做有一个缺点就是int型的字段太过于占空间，我们只需要知道这个号码存在与否，所以最简单的0和1就够用了，能表示0和1的最小存储单位是什么呢？是内存中的一位。BitSet是用于存储二进制位和对二进制进行操作的数据结构。

之前int型的一个电话号码的状态要占4个字节，现在使用BitSet存储出现的电话号码的位置，而且BitSet有自动去重功能。8bit是1byte，int占用4byte，那么使用的空间大小就缩小了4*8 = 32倍。使用了内存大大减少。

下面的简单代码给出了BitSet的例子：

import java.util.BitSet;
public class BitSetDemo {public static void main(String[] args) {//创建一个具有10000000位的bitset　初始所有位的值为falseBitSet bitSet = new BitSet(10000000);//将指定位的值设为truebitSet.set(9999);//或者bitSet.set(9999,true);//输出指定位的值System.out.println("9999:"+bitSet.get(9999));System.out.println("9998:"+bitSet.get(9998));}
}

程序运行结果：第一行输入“true”，第二个输出“false”。

（2）使用BitSet统计随机数的个数

有1千万个随机数，随机数的范围在1到1亿之间。现在要求写出一种算法，将1到1亿之间没有在随机数中的数求出来？

这里以100代替1亿，使用BitSet存放随机数并进行统计，减少内存的使用，代码如下：

import java.util.Random;
import java.util.List;
import java.util.ArrayList;
import java.util.BitSet;
public class BitSetDemo3 {public static void main(String[] args){Random random=new Random();List<Integer> list=new ArrayList<>();for(int i=0;i<100;i++){int randomResult=random.nextInt(100);list.add(randomResult);}System.out.print("0~100之间产生的随机数有:");for(int i=0;i<list.size();i++){System.out.print(list.get(i)+" ");}System.out.println();System.out.println("0~100之间的随机数产生了"+list.size()+"个");BitSet bitSet=new BitSet(100);for(int i=0;i<100;i++){bitSet.set(list.get(i));}//public int cardinality()方法返回此BitSet中比特设置为true的数目//就是BitSet中存放的有效位的个数，如果有重复运算会进行自动去重System.out.println("0~100存在BitSet的随机数有"+bitSet.cardinality()+"个");System.out.print("0~100不在上述随机数中有:");int count = 0;for (int i = 0; i < 100; i++) {if(!bitSet.get(i)){System.out.print(i+" ");count++;}}System.out.println();//0~100不在产生的随机数中的个数就是100减去存在BitSet的随机数个数System.out.print("0~100不在产生的随机数中的个数为:"+count+"个");}
}

运行结果：

（3）使用BitSet查找某个范围内的所有素数的个数

素数：一个大于1的自然数，如果除了1和它本身外，不能被其他自然数整除(除0以外）的数称为素数(质数） ，否则称为合数。

如下为统计2000000以内的素数的个数：

import java.util.BitSet;
public class BitSetDemo3 {public static void main(String[] s){int n = 2000000;long start = System.currentTimeMillis();BitSet sieve = new BitSet(n+1);int count=0;for (int i = 2; i <= n; i++){sieve.set(i);}int finalBit = (int) Math.sqrt(n);for (int i = 2; i < finalBit; i++){if (sieve.get(i)){for (int j = 2 * i; j < n; j += i){sieve.clear(j);}}}int counter = 0;for (int i = 1; i < n; i++) {if (sieve.get(i)) {count++;}}long end = System.currentTimeMillis();System.out.println(count + " primes");System.out.println((end - start) + " ms");}
}

运行结果：

（4）使用BitSet进行排序   

如统计40亿个数据中没有出现的数据，将40亿个不同数据进行排序等。

统计个数和上面两个类似，就不说了。使用BitSet对数据进行排序的代码如下：

import  java.util.BitSet;
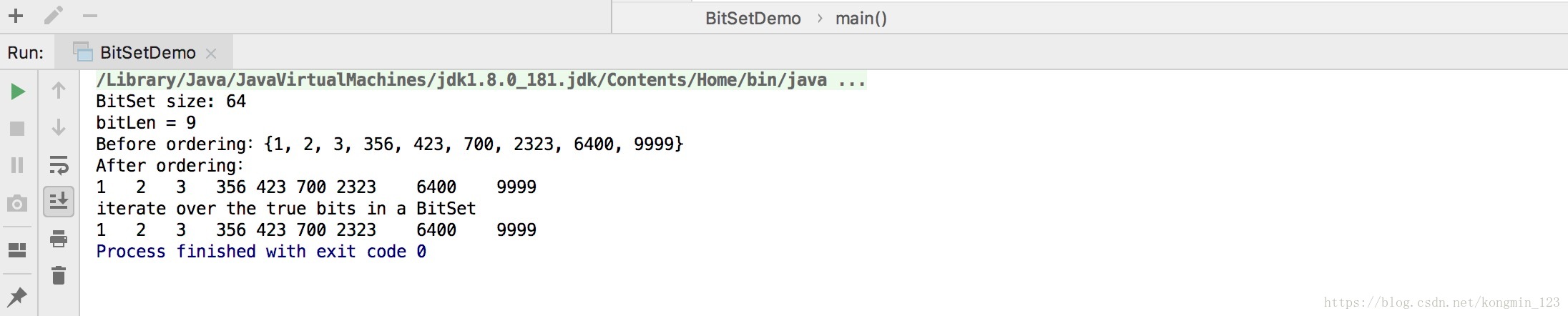
public class BitSetDemo {public static void main(String[] args) {int[] array = new int[] { 423, 700, 9999, 2323, 356, 6400, 1,2,3,2,2,2,2 };BitSet bitSet = new BitSet();//BitSet默认初始大小为64System.out.println("BitSet size: " + bitSet.size());for (int i = 0; i < array.length; i++) {bitSet.set(array[i]);}//public int cardinality()方法返回此BitSet中比特设置为true的数目//就是BitSet中存放的有效位的个数，如果有重复运算会进行自动去重int bitLen=bitSet.cardinality();System.out.println("bitLen = "+bitLen);System.out.println("Before ordering："+bitSet);//进行排序，即把bit为true的元素复制到另一个数组int[] orderedArray = new int[bitLen];int k = 0;//nextSetBit(int fromIndex)方法返回fromIndex之后的下一个值为true的索引//此循环就是按照顺序循环取出在BitSet存在的数，以此达到排序的目的for (int i = bitSet.nextSetBit(0); i >= 0; i = bitSet.nextSetBit(i + 1)) {orderedArray[k++] = i;}System.out.println("After ordering：");for (int i = 0; i < bitLen; i++) {System.out.print(orderedArray[i] + "\t");}System.out.println();//或者顺序访问的数据不放入数组而进行直接读取System.out.println("iterate over the true bits in a BitSet");//或直接迭代BitSet中bit为true的元素for (int i = bitSet.nextSetBit(0); i >= 0; i = bitSet.nextSetBit(i + 1)) {System.out.print(i+"\t");}}
}

运行结果：

（5）使用BitSet求并、交、补集

import  java.util.BitSet;
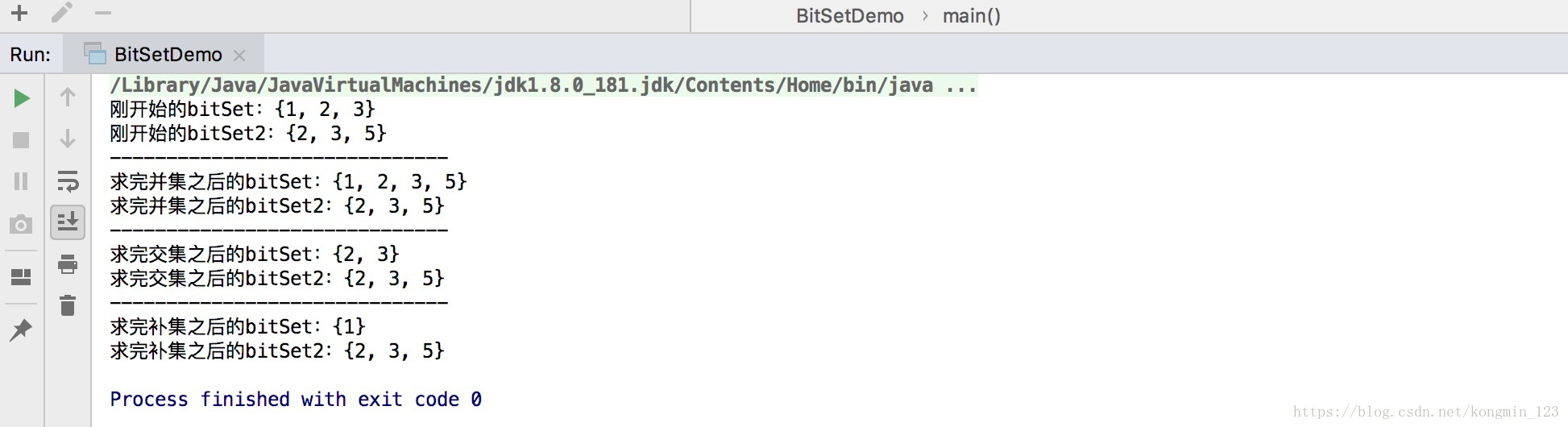
public class BitSetDemo {public static void main(String[] args) {BitSet bitSet = new BitSet(100);bitSet.set(1);bitSet.set(2);bitSet.set(3);BitSet bitSet2 = new BitSet(100);bitSet2.set(2);bitSet2.set(3);bitSet2.set(5);System.out.println("刚开始的bitSet："+bitSet);System.out.println("刚开始的bitSet2："+bitSet2);System.out.println("------------------------------");//求并集bitSet.or(bitSet2);System.out.println("求完并集之后的bitSet："+bitSet);System.out.println("求完并集之后的bitSet2："+bitSet2);System.out.println("------------------------------");//使bitSet回到刚开始的状态bitSet.clear(5);//求交集bitSet.and(bitSet2);System.out.println("求完交集之后的bitSet："+bitSet);System.out.println("求完交集之后的bitSet2："+bitSet2);System.out.println("------------------------------");//使bitSet回到刚开始的状态bitSet.set(1);//此方法返回在bitSet中不在bitSet2中的值，求的是bitSet相对于bitSet2的补集bitSet.andNot(bitSet2);System.out.println("求完补集之后的bitSet："+bitSet);System.out.println("求完补集之后的bitSet2："+bitSet2);}
}

程序运行结果： 

（6）垃圾邮件的识别

这里使用到了布隆过滤器。布隆过滤是一个很长的二进制向量和一系列随机映射函数。

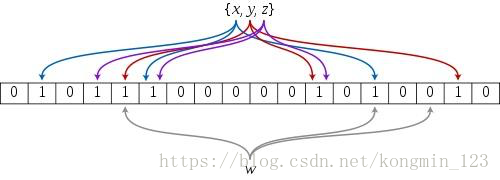
假定我们存储一亿个电子邮件地址，我们先建立一个十六亿二进制（比特），即两亿字节的向量，然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X，我们根据电子邮件地址 X 用八个不同的随机数产生器（F1,F2, ...,F8） 产生八个信息指纹（f1, f2, ..., f8）。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, ...,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。布隆过滤器的结构类似于下图：

假设我们把x、y、z都映射到了布隆过滤器，图中每一个数据对应布隆过滤器，上面介绍的邮件映射的是8位。在使用布隆过滤器进行判断之前首先把所有的数据都映射到布隆过滤器。现在需要判断w是否存在，就根据w找到w应该映射到的布隆过滤器的所有位的位置，如果它对应的所有映射位的位置值都位true，说明w存在，如果有一个以上映射的位的值为fasle,则说明w不存在。

那么如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中？我们用相同的八个随机数产生器（F1, F2, ..., F8）对这个地址产生八个信息指纹 s1,s2,...,s8，然后将这八个指纹对应到布隆过滤器的八个二进制位，分别是 t1,t2,...,t8。如果 Y 在黑名单中，显然，t1,t2,..,t8 对应的八个二进制一定是一。这样在遇到任何在黑名单中的电子邮件地址，我们都能准确地发现。

布隆过滤器决不会漏掉任何一个在黑名单中的可疑地址。但是，它有一条不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址判定为在黑名单中，因为有可能某个好的邮件地址正巧对应个八个都被设置成一的二进制位。好在这种可能性很小。我们把它称为误识概率。在上面的例子中，误识概率在万分之一以下。 

布隆过滤器的好处在于快速，省空间。但是有一定的误识别率。常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

关于BitSet的应用就讲到这里啦。

参考：（1）https://blog.csdn.net/yaoweijq/article/details/5982265   

            （2）https://blog.csdn.net/Allenalex/article/details/10581011   

            （3）https://www.cnblogs.com/xujian2014/p/5491286.html    

            （4）https://blog.csdn.net/jiangnan2014/article/details/53735429    

            （5）http://zfsn.iteye.com/blog/747828     

本文链接：https://my.lmcjl.com/post/3760.html