2023 年第十三届 MathorCup 高校数学建模挑战赛B题解析
- 题目
- 解析
- 前言
- 问题一(晚上更新)
题目
题 城市轨道交通列车时刻表优化问题
列车时刻表优化问题是轨道交通领域行车组织方式的经典问题之一。
列车时刻表规定了列车在每个车站的到达和出发(或通过)时刻,其在实
际运用过程中,通常用列车运行图来表示。图 1 为某一运行图的示例,图
中每一条线表示一趟列车,横轴表示车站,纵轴表示时间,每一条线反映
了一趟列车在不同时刻所处的相对位置,也称为运行线。比如,图中红色
运行线表示,列车于 9:02 分从 D 站出发,于 9:05 分到达 C 站,停留 1
分钟后出发,于 9:09 分到达 B 站,停留 1 分钟后出发,于 10:03 分到达
A 站。
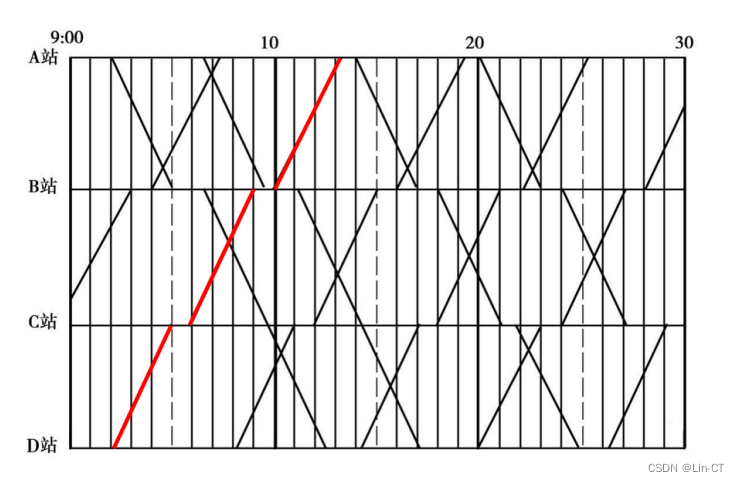
图 1: 列车运行图示意图
实际运营中,在铺画列车运行图之前,首先得先确定列车开行方案,
列车开行方案包括列车编组方案、列车停站方案和列车交路计划三部分。
列车编组方案规定了列车的车型和编组数量(即列车的节数),在本问
题中采用统一的车型和编组数量。
2
列车停站方案是规定列车在哪些站点停站的方案,在本问题中均采用
站站停的停站方案(即列车在每个经过的车站都会停车)。
列车交路计划是指列车在规定的运行线路上往返运行的方式,即规定
了列车在哪些站点之间运行以及开行的数量。大小交路模式是城轨运营中
常用的交路模式,是指城市轨道交通运行线路的长短区间。通俗讲,大交
路是指列车跑完全程,小交路是指将全程中的某两个站作为临时起点或终
点来跑,需要注意的是,只有具有折返能力的车站(能让列车调头的车站)
才能作为交路的起点或终点。图 2 为某大小交路方案示意图,表示以 A 站
为起点的,D 站为终点大交路区间开行 10 对列车,以 A 站为起点,C 站为
终点小交路区间开行 5 对列车。
在大小交路方案中,大小交路列车开行列数通常为 1:n 或 n:1 两种模式,
即每开行 n 列大(小)交路列车后,开行一列小(大)交路列车,并且小
交路所经过的车站数量需有一定限制:小交路区间过短会导致列车的折返
频繁,使运营成本增加;小交路区间过长则无法体现大小交路运营模式的
作用。

图 2: 大小交路示意图
3
在大小交路的运营模式下,乘客通常会被分为 6 种类型,如图 3 所示,
其中 s1− sn为大交路区间,sa − sb为小交路区间。
第Ⅰ,Ⅱ,Ⅲ类乘客起点均位于[s1, sa],终点无论位于哪个区间,乘客
都只能乘坐大交路列车。
第Ⅳ,Ⅴ类乘客起点均位于[sa, sb]。其中第Ⅳ类乘客终点位于[sa, sb],
乘客既可乘坐大交路列车,也可乘坐小交路列车;第Ⅴ类乘客终点位于
[sa, sn],乘客可以乘坐小交路列车之后到sb进行换乘,也可直接乘坐大交路
列车。
第Ⅵ类乘客起点位于[sb, sn],终点位于[sb, sn],乘客只能乘坐大交路
列车。

图 3 :乘客类型分类示意图
在列车开行方案的制定中,需要以最小的企业运营成本和最大的服务
水平(乘客在车时间和乘客等待时间)来满足客流的需求,企业的运营成本包
括固定成本(所需车辆的数量)和变动成本(列车总走行公里)两部分组
成。受到车站通过能力的制约和服务水平的要求,在一定时间内,列车的
发车数量也有一定的限制。
在制定好列车开行方案后,可根据该方案同样以企业运营成本最小化
和服务水平最大化为目标铺画列车运行图,即确定每趟列车的出发和到达
的具体时刻。现有的列车时刻表通常为等间隔的平行运行图,即发车间隔
(如每 5 分钟开行一趟列车)和在同一站点的停站时间相等。发车间隔的
长短会有一定的限制:发车间隔过短,则会影响列车运行的安全;发车间
隔过长,则会增长乘客的平均等待时间,从而影响服务水平。同样地,停
站时间也需受到一定限制,一般来说列车在车站的停站时间正比于在该站
上、下车的乘客数量。另外,需要注意的是,两列车在同一区间追踪运行
时,需保留一定的安全间隔(追踪间隔时间)。
采用大小交路运营模式的列车运行图,大交路列车和小交路列车一般
会交替开行,比如当大交路列车与小交路列车的比例为 2:1 时,则会以每
3 列车为一个组合(前 2 列车为大交路列车,第三列车为小交路列车)滚
动发车。
在下列问题中,只需制定单向的列车时刻表即可。
问题一:在满足客流需求的条件下,以企业运营成本最小化和服务水
平最大化为目标,制定列车开行方案。即确定大交路区间列车的开行数量,
小交路的运行区间以及开行数量。(输出格式详见附件 6)
问题二:在问题一制定的列车开行方案下,同样以企业运营成本最小
化和服务水平最大化且尽量满足客流需求为目标,制定等间隔的平行运行
图。(输出格式详见附件 7,并将附件 7 单独上传到竞赛系统中)
问题三:对于降低企业运营成本和提高服务水平,你们团队有哪些好
的方法或建议?基于客流和车站数据,提供相应的量化分析支持
解析
前言
数学建模主要是让大家构建自己的模型,只要能解决问题的模型就是好模型,无标准答案。我个人的分析过程大致如下文,仅个人观点不一定是正确的,不说太多怕限制了大家的思维哈哈哈
问题一(晚上更新)
本文链接:https://my.lmcjl.com/post/5323.html

4 评论