地球表面的几何模型

地球表面的几何模型是定义合适的地理参照系统的依据。根据大地测量学的研究，球表面几何模型分为四类：

地球的自然表面模型、地球的相对抽象表面模型、地球的旋转椭球体模型和地球的数学模型。

地球的自然表面模型是地球的自然体，起伏而不规则，呈梨形形状 。

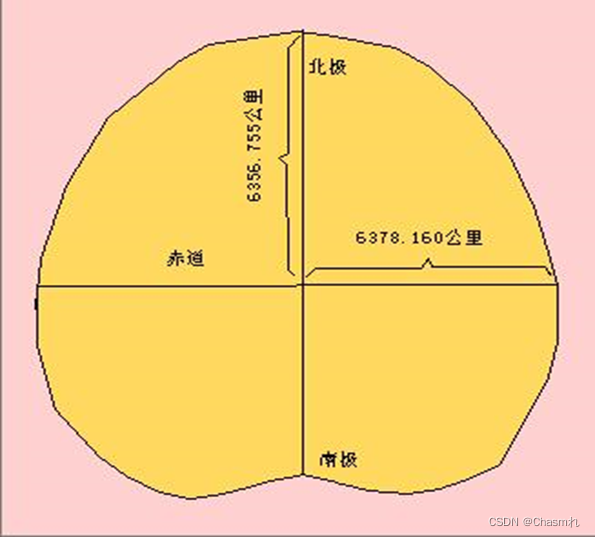
地球自然表面模型

地球的相对抽象表面模型，即由大地水准面描述的模型。是假设当一个海水面处于完全静止的平衡状态时，从海平面延伸到所有大陆下部，且与地球重力方向处处正交的一个连续、闭合的水准面构成的地表模型。以大地水准面为基准，就可以利用水准测量对地球自然表面任意一点进行高程测量。由于地球重力的影响，大地水准面也是一个不规则曲面，但起伏远小于自然表面。

地球的相对抽象表面模型

• 铅垂线：地理空间中任意一点的重力作用线。

• 水准面：自由静止的水面。

• 大地水准面 ：与平均海水面重合，并向大陆、岛屿延伸所形成的封闭曲面

地球的旋转椭球体模型，地球的旋转椭球体模型，是为了测量成果计算的需要，选用一个同大地体相近的、可以用数学方法来表达的旋转椭球来代替地球，且这个旋转椭球是由一个椭圆绕其短轴旋转而成的。它是以大地水准面为基础的。凡是与局部地区(一个或几个国家)的大地水准面符合得最好的旋转椭球，称为参考椭球。

我国测图历史上曾使用的参考椭球：

1、1952年前，海福特椭球；

2、1954年～1980年，克拉索夫斯基椭球，a=6378245m,b=6356863m,f =1:298.3

3、1980年后，1975年国际大地测量学与地球物理学联合会推荐的椭球；

a=6378140m,b=6356755m,f=1:298.257

4、WGS1984，a=6378137m,b=6356752m

地球的数学模型，地球的数学模型，是在解决其它一些大地测量学问题时提出来的，如类地形面、准大地水准面、静态水平衡椭球体等，GIS中的坐标系定义是GIS系统的基础，正确定义GIS系统的坐标系非常重要。GIS中的坐标系定义由基准面和地图投影两组参数确定，而基准面的定义则由特定椭球体及其对应的转换参数确定，因此欲正确定义GIS系统坐标系，首先必须弄清地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者之间的关系。

地球椭球体只不过是一个具有长半轴，短半轴和变率的椭球体，可以任意放置的，它没有为我们规定度量的起点，所以就有基准面的产生，而基准面就是规定了度量标准。

基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面.椭球体与基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，一般意义上基准面与参考椭球体是同一个概念。

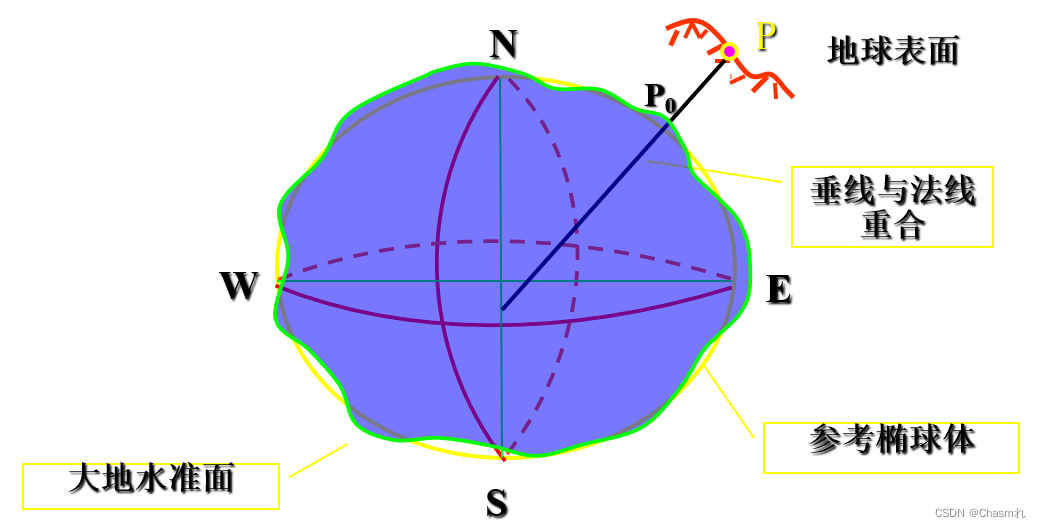
参考椭球面与我国大地原点

地面上选一点P，由P点投影到大地水准面P0点,使P0上的椭球面与大地水准面相切， 此时过P0点的铅垂线与P0点的椭球面法线重合，切点P0称为大地原点。同时要使旋转椭球短轴与地球短轴相平行（不要求重合），达到本国范围内的大地水准面与椭球面十分接近，该椭球面称为参考椭球面。我国大地原点选在我国中部陕西省泾阳县永乐镇。

地球椭球的参数可用a(长半径)、b（短半径）及α（扁率）表示。扁率α为α=a-b/a,1979年国际大地测量与地球物理联合会推荐的地球椭球参数a=6378140m，b=6356755.3m, α=1:298.257。

旋转椭球面是数学表面，可用如下的公式表示：

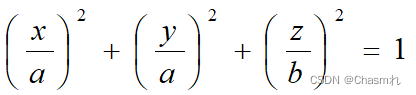
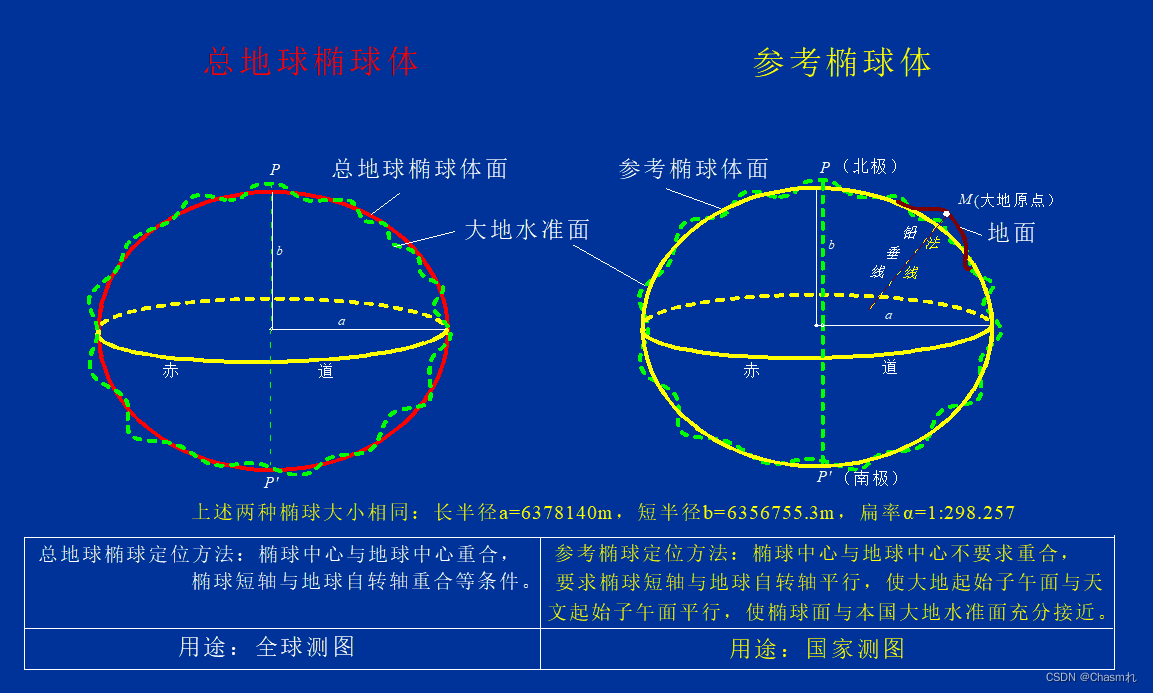
按一定的规则将旋转椭球与大地体套合在一起，这项工作称椭球定位和定向。定位时采用椭球中心与地球质心重合，椭球短轴与地球短轴重合，椭球与全球大地水准面差距的平方和最小，这样的椭球称总地球椭球。

总地球椭球与参考椭球（水准面）的区别

地理信息系统常用的地图投影

高斯-克吕格投影

高斯－克吕格投影实质上是横轴切圆柱正形投影。

该投影是等角横切椭圆柱投影。想象有一椭圆柱面横套在地球椭球体外面，并与某一条子午线（称中央子午线或轴子午线）相切，椭圆柱的中心轴通过椭球体中心，然后用一定的投影方法将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上，再将此柱面展开即成为投影面。

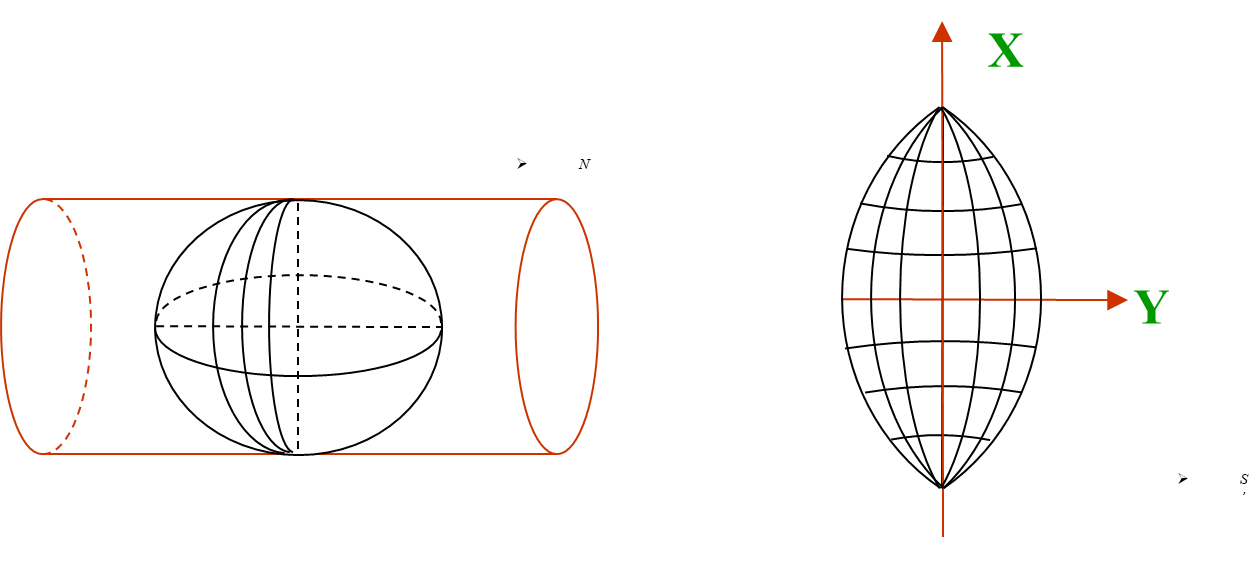
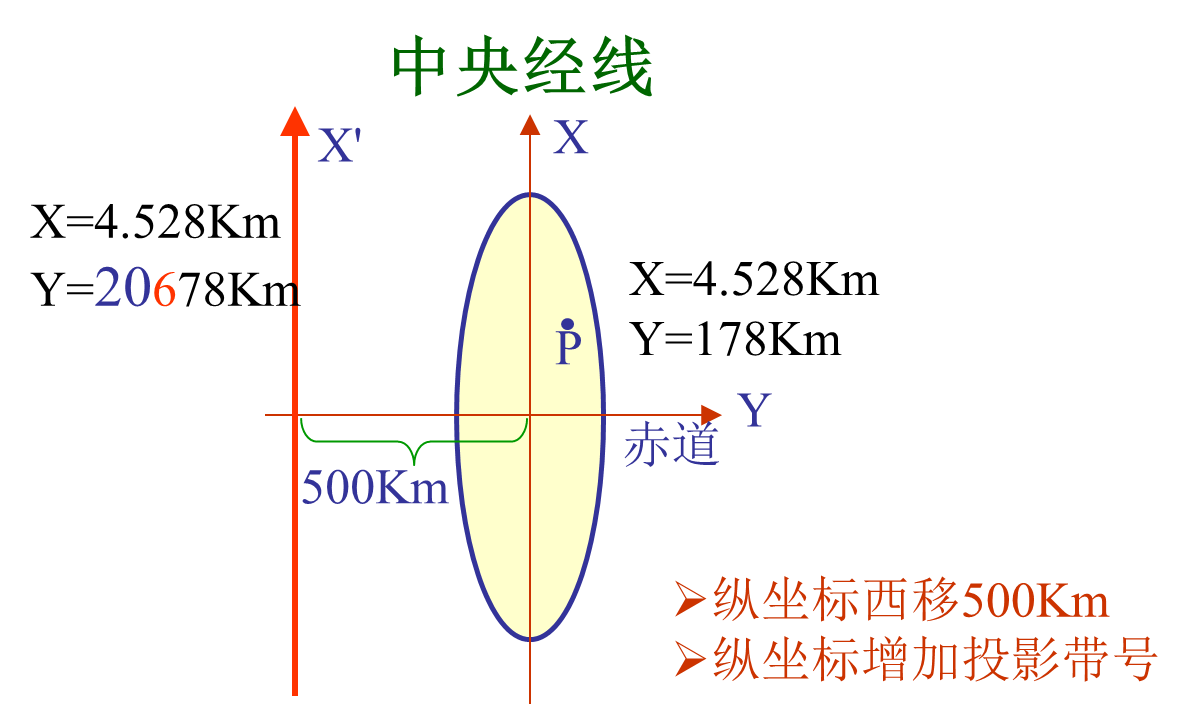
高斯平面直角坐标系以中央经线和赤道投影后为坐标轴，中央经线和赤道交点为坐标原点，纵坐标由坐标原点向北为正，向南为负，规定为 X轴，横坐标从中央经线起算，向东为正，向西为负，规定为Y轴。所以，高斯-克吕格坐标系的X、Y轴正好对应一般GIS软件坐标系中的Y和X。

高斯投影的条件

• 中央经线和赤道投影后为互相垂直的直线，且为投影的对称轴

• 投影具有等角性质

• 中央经线投影后保持长度不变

高斯投影的特点

• 中央子午线长度变形比为1，其他任何点长度比均大于1

• 在同一条经线上，长度变形随纬度的降低而增大，在赤道处为最大

• 在同一条纬线上，离中央经线越远，变形越大，最大值位于投影带边缘

• 投影属于等角性质，没有角度变形，面积比为长度比的平方

• 长度比的变形线平行于中央子午线

高斯投影6°和3°带分带

为了控制变形，我国地图采用分带方法。我国1：1.25万—1：50万地形图均采用6度分带，1：1万及更大比例尺地形图采用3度分带，以保证必要的精度。

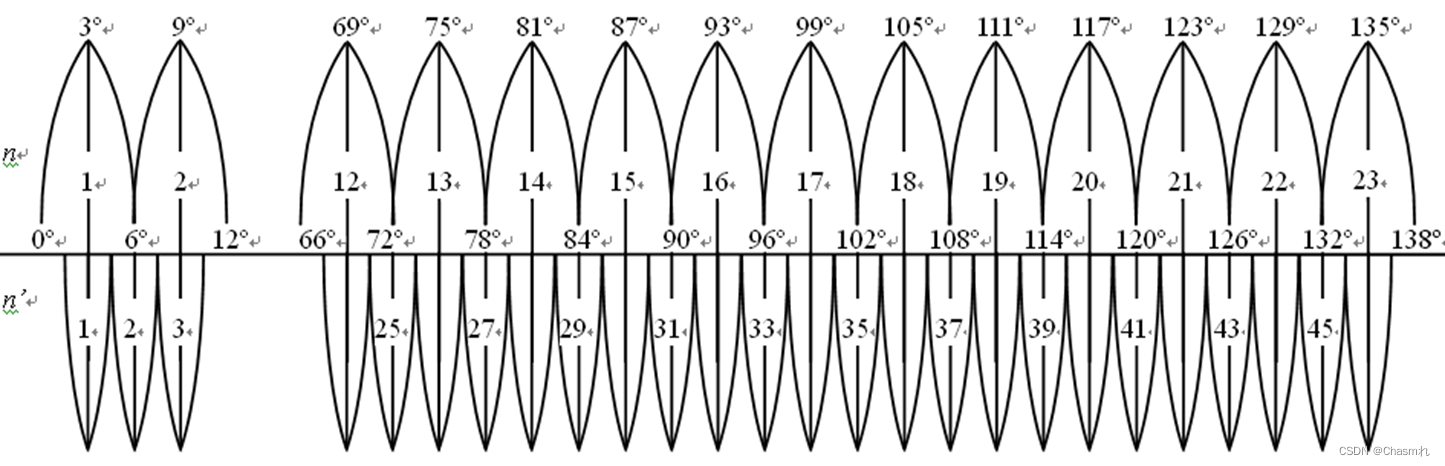
6度分带从格林威治零 度经线起，每6度分为一个投影带，该投影将地区划分为60个投影带，已被许多国家作为地形图的数字基础。一般从南纬度80到北纬度84度的范围内使用该投 影。

3度分带法从东经1度30分算起，每3度为一带。这样分带的方法在于使6度带的中央经线均为3度带的中央经线；在高斯克吕格6度分带中中国处于第13 带到23带共12个带之间；在3度分带中，中国处于24带到45带共22带之间。

高斯--克吕格投影的优点

• 等角性别适合系列比例尺地图的使用与编制;

• 径纬网和直角坐标的偏差小，便于阅读使用;

• 计算工作量小，直角坐标和子午收敛角值只需计算一个带。

• 由于高斯-克吕格投影采用分带投影，各带的投影完全相同，所以各投影带的直角坐标值也完全一样，所不同的仅是中央经线或投影带号不同。为了确切表示某点的位置，需要在Y坐标值前面冠以带号。如表示某点的横坐标为米，前面两位数字“20”即表示该点所处的投影带号

墨卡托投影

• 定义 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

• 特性 墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

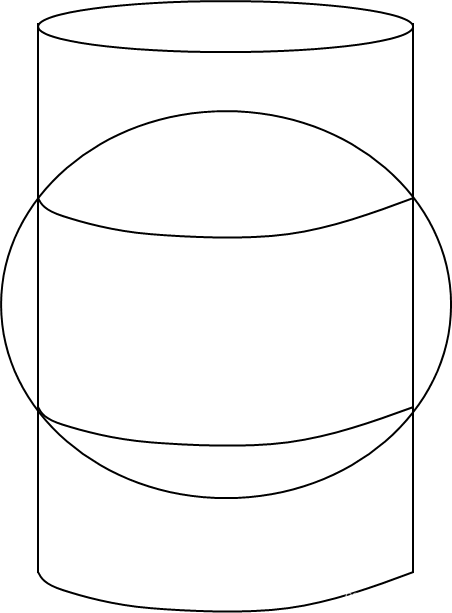
墨卡托等角正切圆柱投影

墨卡托投影的用途

在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

海底地形图编绘规范”（GB/T 17834-1999，海军航保部起草）中规定1：25万及更小比例尺的海图采用墨卡托投影，其中基本比例尺海底地形图（1：5万，1：25万，1：100万）采用统一基准纬线30°，非基本比例尺图以制图区域中纬为基准纬线。基准纬线取至整度或整分。

UTM投影（通用墨卡托投影）

该投影为横轴等角割圆柱投影，可以改善高斯投影，用圆柱割地球于两条等高圈上，投影后这两条割线上没有变形，但离开这两条割线越远则变形越大，在两条割线以内长度变为负值，在两条割线意外长度变为正值。

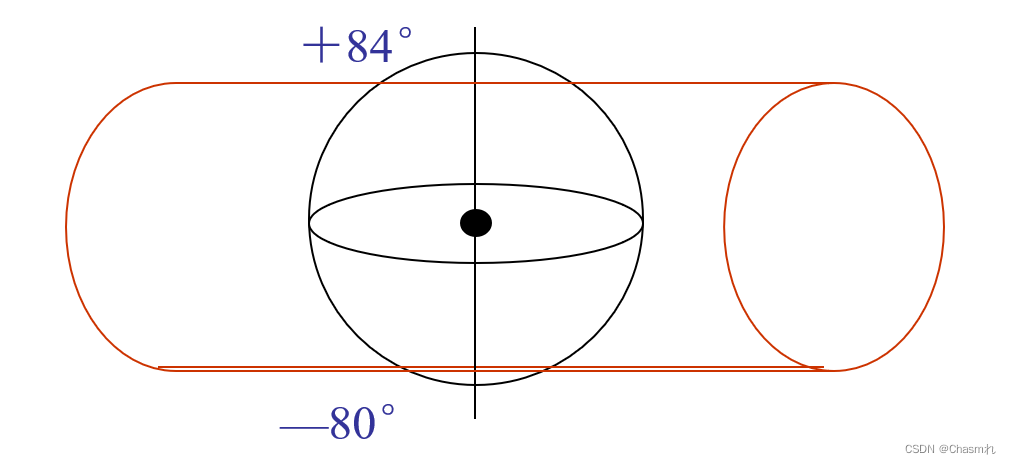
UTM投影（通用墨卡托投影）

UTM投影特点和用途

特点：

• 中央子午线长度变形比为0.9996

• 该投影将世界划分为60个投影带，每带经度差为6度，已被许多国家作为地形图的数字基础

• 投影带编号为1,2,3…60连续编号，第1带在177°W和180°W之间，且连续向东计算

• 其它同高斯投影

用途：UTM投影已经被许多国家和地区采用作为地形图的数学基础，其中有美国、日本、加拿大、泰国、阿富汗、巴西、法国和瑞士等约80个国家。有的国家局部采用UTM投影作为地图数学基础。我国的卫星影像资料常采用UTM投影。

兰勃特投影（正轴等角割圆锥投影）

设想用一个圆锥正割于球面两条标准纬线，应用等角条件将地球面投影到圆锥面上，然后沿圆锥一条母线剪开，展开即为兰勃特投影平面。兰勃特等角投影后纬线为同心圆弧，经线为同心圆半径。

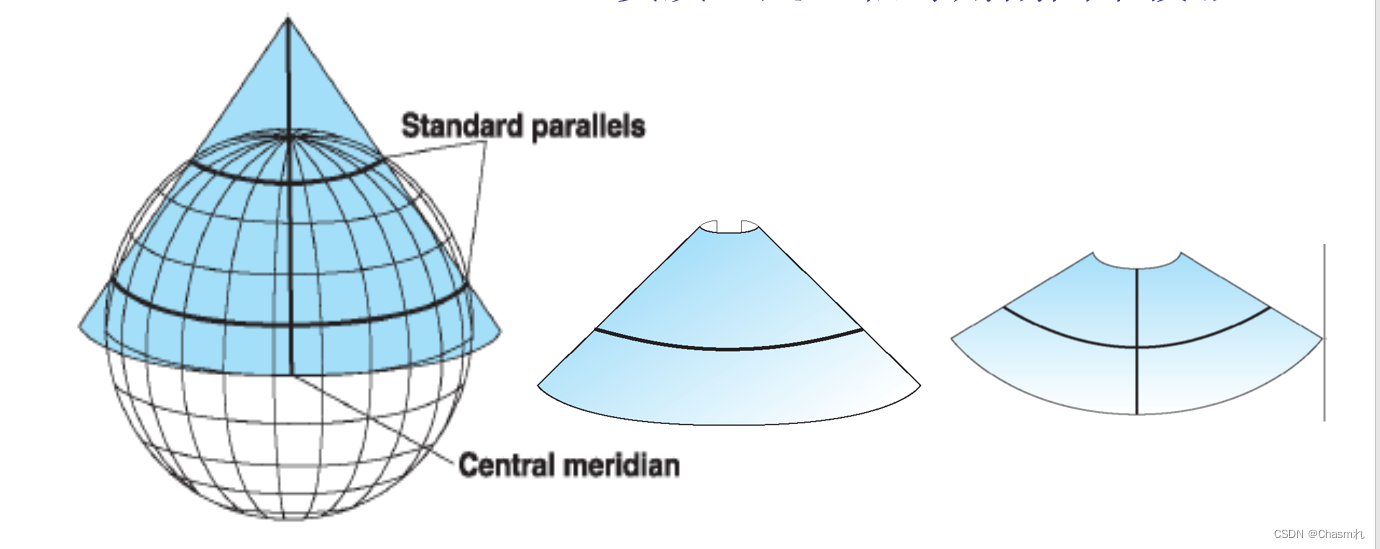
兰勃特投影的变性分布规律

角度没有变形

两条标准纬线上没有任何变形

等变形和纬线一致，即痛一条纬线上的变形处处相等

在同一经线上，两标准纬线外侧为整变形（长度比大于1），而两标准纬线之间为负变形（长度比小于1）。变形比较均匀，变形绝对值也比较小

同一纬线上等经差的线段长度相等，两条纬线间的经纬线长度处处相等

阿尔伯斯投影（正轴等面积投影）

为双标准纬线投影，也即正轴等面积割圆锥投影。与兰勃特投影属于同一投影族。该投影经纬网的经线为辐射直线，纬线为同心 圆圆弧。两条割纬线投影后无任何变形。投影区域面积保持与实地相等。

Albers投影的应用在编制一些行政区划图、人口地图、地势图等方面应用较广。

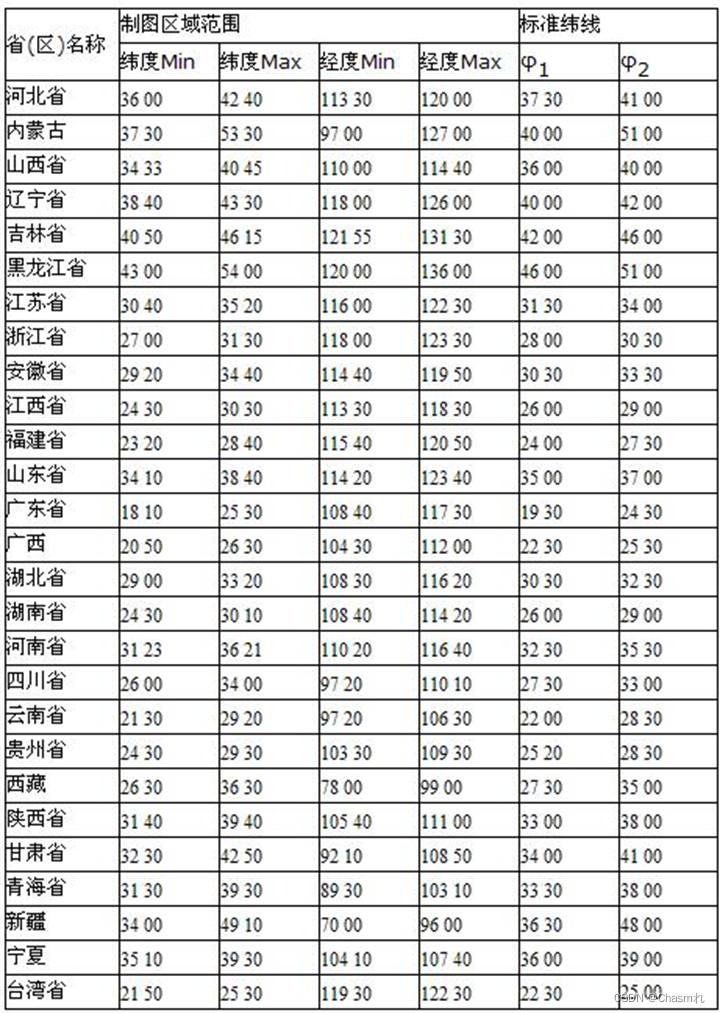
由于我国位于中纬度地区，中国地图和分省地图经常采用割圆锥投影（ Albers 或Lambert投影），中国地图的中央经线常位于东经105度(110度)，两条标准纬线分别为北纬25度和北纬47度，而各省的参数可根据地理位置和轮廓形状初步加以判定。例如甘肃省的参数为：中央经线为东经101度，两条标准纬线分别为北纬34度和41度。

我国目前各省（区）按制图区域单幅地图选择投影时，所采用的两条标准纬线

北京市、天津市标准纬线同河北省，上海市标准纬线同江苏省。

南海诸岛采用正圆柱投影。

投影的选择

正轴圆锥投影和圆柱投影最适宜于沿纬线伸展的地区，特别是正轴圆锥投影适宜于中纬度地区，正轴圆柱投影最适宜于低纬度和赤道地区。

横轴圆柱投影适宜于沿经线伸展的地区。

中国分省（区）地图投影的选择：从制图区域的形状和位置来看：我国绝大多数省（区）处于中纬度地区，因此最适宜采用圆锥投影；对于个别省区，如广东省包括南海诸岛及南中国海域，它位于赤道附近地区，可采用正轴圆柱投影；对于经差较小的地区，亦可采用高斯—克吕格投影。即正轴等角圆锥投影；正轴等角割圆柱投影；宽带高斯—克吕格投影。

中国常用的地图投影举例

（1）世界地图的投影：正轴等角割圆柱投影

（2）半球地图的投影：

东半球图：横轴等积方位投影φ0=0，λ0=±70

横轴等角方位投影φ0=0，λ0=±70

西半球图：横轴等积方位投影φ0=0，λ0=-110

横轴等角方位投影φ0=0，λ0=-110

南北半球地图： 正轴等距离方位投影、正轴等角方位投影、正轴等面积方位投影 (3) 中国全图（南海诸岛作插图）

正轴等面积割圆锥投影:两条标准纬线曾采用 φ1=24 00，φ2=48 00 或 φ1=25 00，φ2=45 00 或 φ1=23 30，φ2=48 30.

目前常采用 φ1=25 00，φ2=47 00

(4)亚洲地图的投影：

斜轴等面积方位投影 φ0=+40，λ0=+90；φ0=+40，λ0=+85

彭纳投影 φ0=+40，λ0=+80；φ0=+30，λ0=+80

常用知识点说明

角度弧度转换

double degrees = (180 / Math.PI) * radians;//弧度转角度

double radians = (Math.PI / 180) * degrees;//角度转弧度

GIS经纬度小数点对应米

经度小数点

纬度小数点后五位

影像瓦片级别对应精度(天地图)

高程级别对应瓦片精度

各省坐标范围

本文链接：https://my.lmcjl.com/post/5434.html