一、信道的定义与调制信道的数学模型
1.信道的定义与分类
信道（Channel）是指以传输媒质为基础的信号通道。根据新到的定义，如果信道仅是指信号的传输媒质，这种信道称为狭义信道；如果这种信道不仅是传输媒质，而且包括通信系统中的转换装置，这种信道称为广义信道。
狭义信道按照传输媒质的特性可分为有线信道和无线信道。有线信道包括对称电缆、同轴电缆及光纤等。无线信道包括地波传播、短波电离层反射、超短波、移动无线电信道等。常把广义信道简称为信道。
广义信道按照它包括的功能可分为调制信道（Modulated Channel）、编码信道（Coding Channel）等。
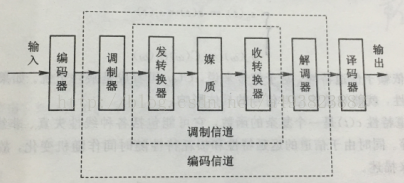
2.调制信道模型
调制信道可以用一个二端口（或多端口）线性时变网络来表示，这个网络便称为调制信道模型。
二端口的调制信道模型，其输出与输入的关系有：
根据信道传输函数C(w)的时变特性不同可以分两大类：
设网络函数为H(w)
①C(w)基本不随时间变化，即信道对信号的影响是固定的或变化极为缓慢的，这类信道称为恒定参量信道，简称恒参信道。
②C(w)随时间随机快变化，这类信道称为随机参量信道，简称随参信道。
二、恒参信道与随参信道
信道特性主要由传输媒质所决定，如果传输媒质是基本不随时间变化的，所构成的广义信道通常属于恒参信道；如果传输媒质随时间随机快变化，则构成的广义信道通常属于随参信道。
1.恒参信道
如由电缆、中长波地波传播。超短波及微博视距传播、人造卫星中继、光导纤维以及光波视距传播等传输媒质构成的广义信道都属于恒参信道。
设K0为传输系数，td为时间延迟（均为常数），则恒参信道的传输特性为：
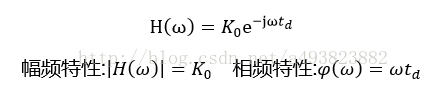
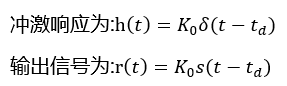
由此可见，理想恒参信道对信号传输的影响是：
①对信号在幅度上产生固定的衰减
②对信号在时间上产生固定时延
这种情况也称信号是无失真传输。
2.随参信道
随参信道是指信道传输特性随时间随机快速变化的信道。常见的随参信道有陆地移动信道、短波电离层反射信道、超短波及微波对流层散射信道以及超短波超视距绕射等信道。
随参信道的传输媒质具有以下三个特点：
①对信号的衰耗随时间随机变化；
②信号传输的时延随时间随机变化
③多径传播
三、三种信道衰落模型
0.什么是衰落（fading）
对于S——D这样一个发送接收系统来说，理想的无线信号传播（自由空间传播模型）是由S发送的电磁信号经过一定的衰减（attenuation）到达D点，我们可以理解为信号沿着S—D的直线。虽然这样，电磁波实际上是以球面波的形式向周围360度辐射，但其是只有沿着S—D直线传播的信号才能抵达D点，我们也可以把S—D路径称为直射路径。这是对于自由空间来说的，在自由空间模型里面除了S和D什么也没有。
而对于实际的大气传播环境，大气中包含着许多的小颗粒（悬浮物），或者小粒子。从S出发，沿着非S—D方向的其它传播方向的额电磁波可能经过一系列的反射（散射）后而抵达接收端D，我们把这种路径称为散射路径。由于每一条散射路径经历的路程都不一样，这样，他们抵达接收端的相位各不相同，导致总的信号强度变低。这样我们把由于信号经过了多个路径而抵达接收端导致信号强度发生随机变化的现象称为衰落（fading）。
1.瑞利衰落信道模型 （Rayleigh）
假设发送信号为单一频率正弦波，即
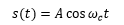
若不考虑直射路径，多径信道共有n条路径，各条路径具有时变衰耗和时变传输时延，且从各条路径到达接收端的信号相互独立，则接收端接受到的合成波为
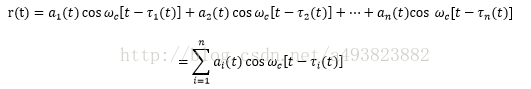
式中，ai(t)为从第i条路径到达接收端的信号振幅，τi(t)为第i条路径的传输时延。传输时延可以转换为相位的形式，即
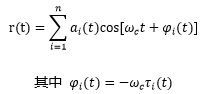
为从第i条路径到达接收端的信号的随机相位。
r(t)也可表示为如下形式：
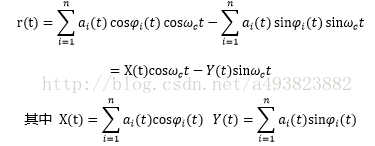
由于X(t)和Y(t)都是相互独立的随机变量之后，根据中心极限定理，大量独立随机变量之和的分布趋于正态分布。因此，当n足够大时，X(t)和Y(t)都趋于正态分布。通常情况下X(t)和Y(t)的均值为0（由于没有直射路径），方差相等。这种表示方式也叫做同相-正交表示法。
r(t)也可以表示为如下形式：
这种表达方式也称包络-相位表示法。易知V(t)的一维分布服从瑞利分布，相位φ(t)的一维分布服从均匀分布。可表示为：
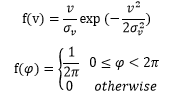
由于包络服从瑞利分布，故其称为瑞利信道模型。
对于陆地移动信道、短波电离层反射等随参信道，其路径幅度ai(t)和相位函数φi(t)随时间变化与发射信号载波频率相比要缓慢得多。因此，相对于载波来说V(t)和φ(t)是慢变化随机过程，于是r(t)可以看成是一个窄带随机过程。由此得出以下两个结论：
①多径传播使单一的正弦信号变成了包络和相位受调制的窄带信号，这种信号称为衰落信号，即多径传播使信号产生瑞利型衰落（多径衰落）。
②从频谱上看，多径传播使单一谱线变成了窄带频谱，即多径传播引起了频率弥散。
2.莱斯衰落信道模型（Rician）
当信道中存在一个固定的直射分量时，X(t)与Y(t)的均值不再为0。其接收信号是复高斯信号和直射分量的叠加（即正弦波加窄带高斯过程），其包络的概率密度函数服从莱斯分布，即下式
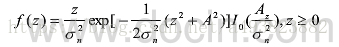
瑞利与莱斯分布于窄带高斯过程详见瑞利、莱斯分布于窄带高斯过程
https://blog.csdn.net/a493823882/article/details/78265414
3.Nakagami-m信道衰落模型
瑞利和莱斯分布与实验数据有时不太吻合，因此人们提出了能吻合更多实验数据的一种更通用的信道衰落分布，就是Nakagami-m衰落，其分布为下式
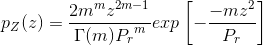
Pr为平均功率，T(m)为伽马函数，m为衰落参数。m=1时，上式退化为瑞利衰落；令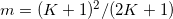
，则上式近似为衰落参数为K的瑞利衰落；m=∞m=\inftym=∞代表无衰落。改变m的值，Nakagami衰落还可以转变为多种衰落模型。
————————————————
版权声明：本文为CSDN博主「Norstc」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/a493823882/article/details/78264608
本文链接：https://my.lmcjl.com/post/7792.html
4 评论