论文地址：https://arxiv.org/pdf/2203.15556.pdf

一、简介

​ 近期出现了一些列的大语言模型(Large Language Models, LLM)，最大的稠密语言模型已经超过了500B的参数。这些大的自回归transformers已经在各个任务上展现出显著效果。

​ 训练LLM的计算和能源消耗是巨大的，并且随着模型尺寸的增加而增加。实际中，分配的计算预算是提前知道的：有多少机器可用以及我们想使用它们多久。通常训练LLM只会训练一次，在给定计算预算的情况下准确估计最优模型的超参数是至关重要的。

​ Kaplan et al.(2020)展示了自回归语言模型的参数数量和其表现有着幂律关联。因此，该领域训练的模型越来越大，并期望来改善模型效果。Kaplan et al.(2020)的一个显著结论是，不应该将大模型训练至最低的可能loss来获得计算最优。我们也得到了同样的结论，但我们估计大模型应该比作者推荐训练更多的tokens。具体来说，给定10倍的计算预算，他们建议模型尺寸应该增加5.5倍，而训练的tokens数量应该增加1.8倍。相反，我们发现模型的尺寸和训练的tokens应该等比例的增加。

​ 遵循Kaplan et al.的工作和GPT-3的训练设置，许多近期训练的大语言模型在接近300B的tokens上训练，符合随着计算量的增加而增加模型大小的方法。

​ 在本文中，我们重新审视问题：*给定固定的FLOPs预算，如何折中模型尺寸和训练tokens的数量？*为了回答这个问题，我们将最终的预训练损失函数L(N,D)L(N,D)L(N,D)定义为模型参数量N和训练tokens数量D的函数。因为计算预算C是所见训练tokens和模型参数的固定函数FLOPs(N,D)\text{FLOPs}(N,D)FLOPs(N,D)，我们感兴趣的是在约束FLOPs(N,D)=C\text{FLOPs}(N,D)=CFLOPs(N,D)=C下最小化LLL：
Nopt(C),Dopt(C)=argminN,Ds.t.FLOPs(N,D)=CL(N,D)(1)N_{opt}(C), D_{opt}(C) = \mathop{\text{argmin}}_{N,D s.t. \text{FLOPs}(N,D)=C} L(N,D) \tag{1} Nopt​(C),Dopt​(C)=argminN,Ds.t.FLOPs(N,D)=C​L(N,D)(1)
函数Nopt(C)N_{opt}(C)Nopt​(C)和Dopt(C)D_{opt}(C)Dopt​(C)描述了计算代价C的最优分配。我们基于400个模型的损失值来评估这些函数，模型参数从70M至16B，并且在5B至400B tokens上训练。我们的方法带来了与Kaplan et al.不同的结果。上图1展示了这些结果。

​ 基于我们估计的计算最优边界，我们预测了训练Gopher所有的计算代价，最优模型应该小4倍并且在多4倍的tokens上进行训练。我们通过训练一个计算高效的70B模型验证了这个想法，称为Chinchilla，在1.4万亿tokens上训练。Chinchilla不仅优于更大的Gopher，并且减少的模型尺寸能够降低推理的代价，并且极大的促进了在较小硬件上的下游应用。LLM的能源成本可以通过推理来分摊。

二、评估最优参数/训练tokens分配

​ 我们提出三种不同的方法来回答驱动我们研究的问题：*给定固定的FLOPs预算，如何折中模型的尺寸和训练tokens数量？*在这三种情况下，我们都从训练一系列模型开始，这些模型的大小和训练tokens的数量都不同。然后，使用训练结果曲线来拟合一个应该如何缩放的估计器。我们假设计算和模型尺寸有着幂律关系；尽管未来的工作可能希望在这种关系中包含潜在的曲律关系。三种方法的结果预测相似，建议模型参数量和训练tokens数量应该随着计算的增加而等比例增加。

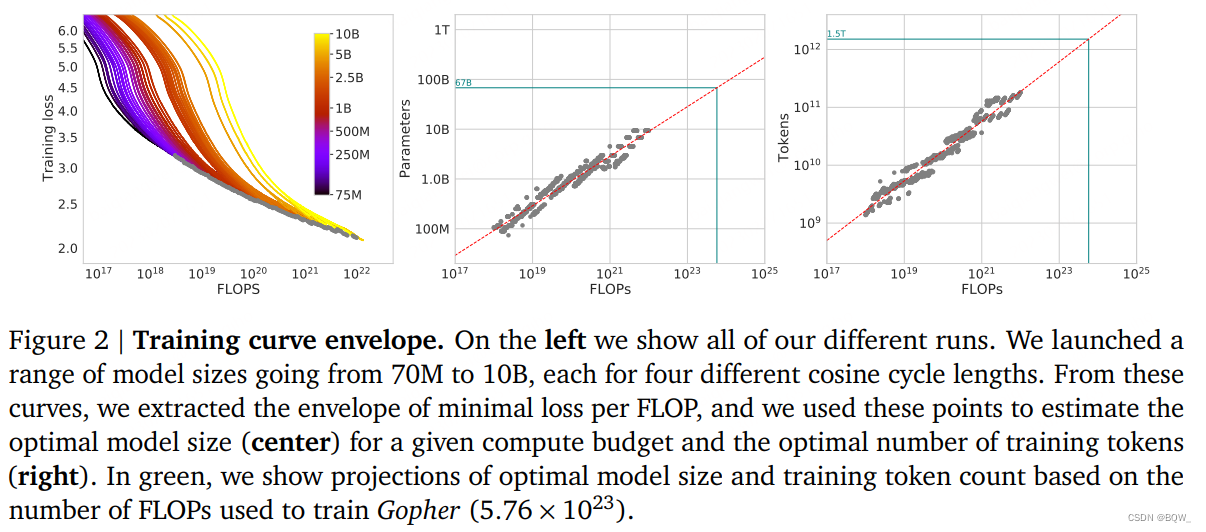
1. 方法一：固定模型尺寸并改变训练tokens的数量

​ 第一个方法，固定模型尺寸并改变训练的steps，以4种不同数量的训练序列来训练每个模型。在这些训练中，对于给定的训练FLOPs数量来说，我们能够直接抽取一个可以实现最小loss的估计值。

​ 对于每个固定的参数量N，训练4个不同的模型。然后，对于每次训练的结果进行平滑并插值至训练损失值曲线中。这样就获得了从FLOP数量至训练损失值的连续映射。然后，对于每个FLOP数量确定出最低的损失值。使用这些插值能够获得从任意FLOP数量C至最高效模型尺寸N和训练token数量D的映射FLOPs(N,D)=C\text{FLOPs}(N,D)=CFLOPs(N,D)=C。在1500个FLOP值的对数间隔中，我们发现了所有模型中能够达到损失最小的模型尺寸和训练所需token数量。最终，我们拟合幂律来估计给定计算总量情况下的最优模型尺寸和训练tokens数量(见上图2的中间和右边)，获得了关系Nopt∝CaN_{opt}\propto C^aNopt​∝Ca和Dopt∝CbD_{opt}\propto C^bDopt​∝Cb。我们也发现，a=0.50a=0.50a=0.50和b=0.50b=0.50b=0.50。

2. 方法二：固定FLOPs总量

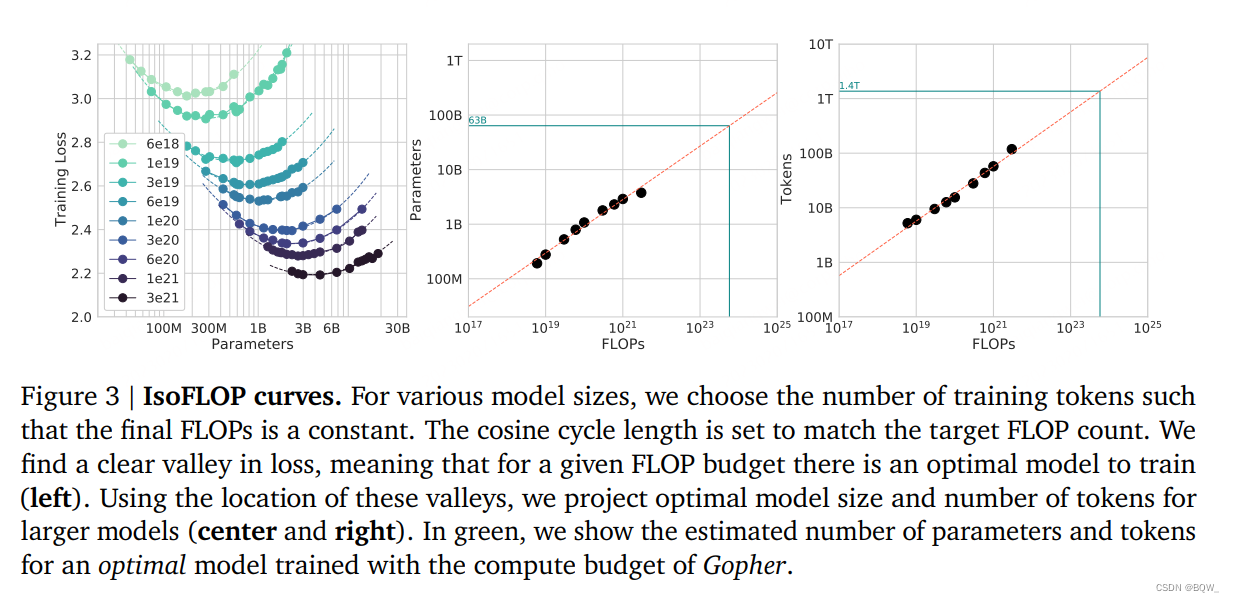
​ 第二种方法，我们选择9个不同的训练FLOP数量，并改变模型尺寸(从6×10186\times 10^{18}6×1018至3×10213\times 10^{21}3×1021)。针对每个点来考虑最终的训练loss。这允许我们直接回答问题：对于给定的FLOP预算，最优参数量是多少？

​ 对于每个FLOP预算，上图3(左)中绘制了参数量和最终损失函数值的关系。在所有的例子中，我们确保已经训练了足够多样的模型尺寸集合，来发现一个loss的明确最小值。我们为每个独立的FLOP拟合一个抛物线来直接估计哪种模型尺寸能够最小化loss(上图3左)。同前面的方法一样，我们也以幂律来拟合了FLOPs和最优loss的模型尺寸和训练tokens的数量，如上图3中、右所示。我们再一次拟合了指数形式Nopt∝CaN_{opt}\propto C^aNopt​∝Ca和Dopt∝CbD_{opt}\propto C^bDopt​∝Cb，我们发现a=0.49a=0.49a=0.49和b=0.51b=0.51b=0.51。

3. 方法三：拟合一个参数化损失函数

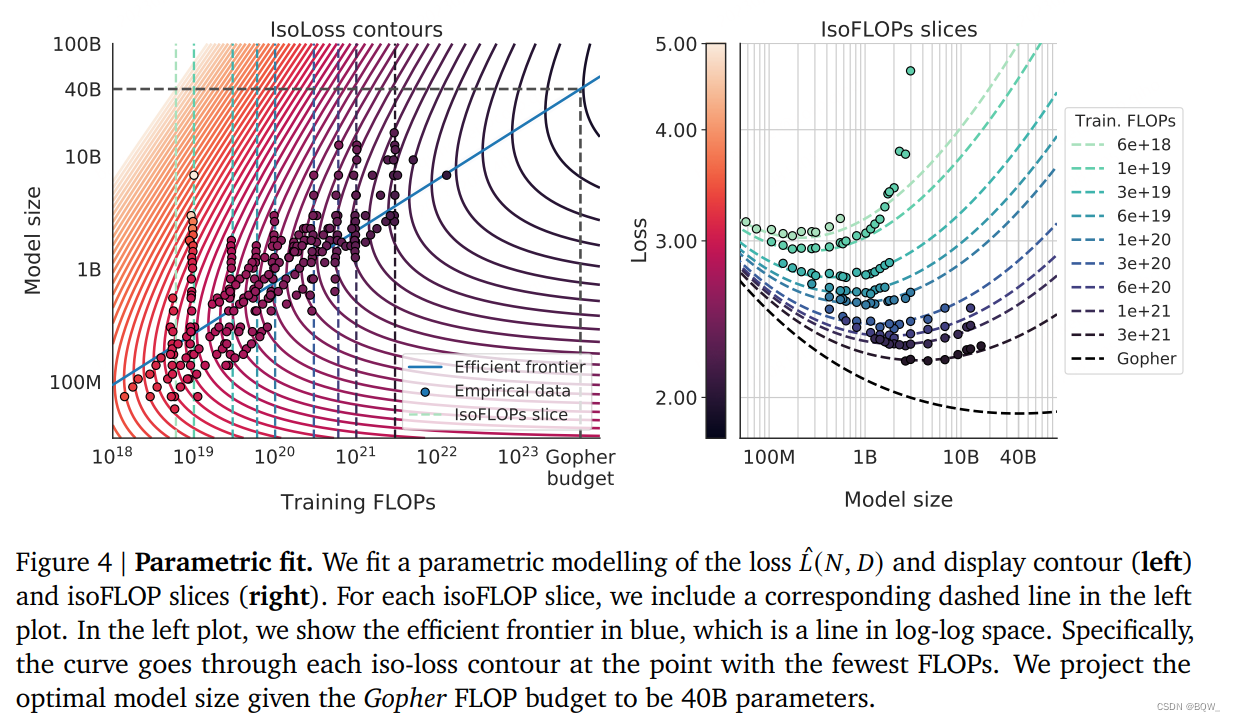
​ 最终，我们从方法1&2实验中建模所有最终的损失值为模型参数量和所见token数量的参数化函数。遵循经典的风险分解，我们提出下面的函数形式
L^(N,D)≜E+ANα+BDβ(2)\hat{L}(N,D)\triangleq E+\frac{A}{N^\alpha}+\frac{B}{D^{\beta}} \tag{2} L^(N,D)≜E+NαA​+DβB​(2)
第一项捕获了在数据分布上一个理想生成过程的loss，其应该对应于自然文本的熵。第二项捕获了：一个具有参数N且完美训练的transformer不如理想情况的过程。最后一项捕获了：没有经过训练收敛的transformer，因为我们仅对数据分布中的一些样本进行了有效的优化步数。

​ 模型拟合。为了估计(A,B,E,α,β)(A,B,E,\alpha,\beta)(A,B,E,α,β)，我们使用L-BFGS算法来最小化预测值和观察值的Huber loss：
min⁡A,B,E,α,β∑Runs iHuberδ(log⁡L^(Ni,Di)−log⁡Li)(3)\min_{A,B,E,\alpha,\beta}\sum_{\text{Runs i}}\text{Huber}_{\delta}(\log\hat{L}(N_i,D_i)-\log L_i) \tag{3} A,B,E,α,βmin​Runs i∑​Huberδ​(logL^(Ni​,Di​)−logLi​)(3)
我们通过从初始化网格中选择最优拟合来达到可能的局部最小值。Huber loss对于异常值鲁棒，我们发现这对于保持留出数据点的良好预测性非常重要。

​ 有效边界。我们在约束FLOPs(N,D)≈6ND\text{FLOPs}(N,D)\approx 6NDFLOPs(N,D)≈6ND下通过最小化参数化的损失函数L^\hat{L}L^来近似函数NoptN_{opt}Nopt​和DoptD_{opt}Dopt​。得到的NoptN_{opt}Nopt​和DoptD_{opt}Dopt​平衡了等式(3)中依赖于模型尺寸和数据的两项。通过构造，其具有幂律形式。
Nopt(C)=G(C6)2,Dopt(C)=G−1(C6)bN_{opt}(C)=G\Big(\frac{C}{6}\Big)^2,\quad D_{opt}(C)=G^{-1}\Big(\frac{C}{6}\Big)^b Nopt​(C)=G(6C​)2,Dopt​(C)=G−1(6C​)b
其中，
G=(αAβB)1α+β,a=βα+β,b=αα+β(4)G=\Big(\frac{\alpha A}{\beta B}\Big)^{\frac{1}{\alpha+\beta}},\quad a=\frac{\beta}{\alpha+\beta},\quad b=\frac{\alpha}{\alpha+\beta} \tag{4} G=(βBαA​)α+β1​,a=α+ββ​,b=α+βα​(4)
我们在上图4(左)中展示了集合函数L^\hat{L}L^的轮廓。对于这种方法，我们发现a=0.46a=0.46a=0.46和b=0.54b=0.54b=0.54。

4. 最优模型尺寸

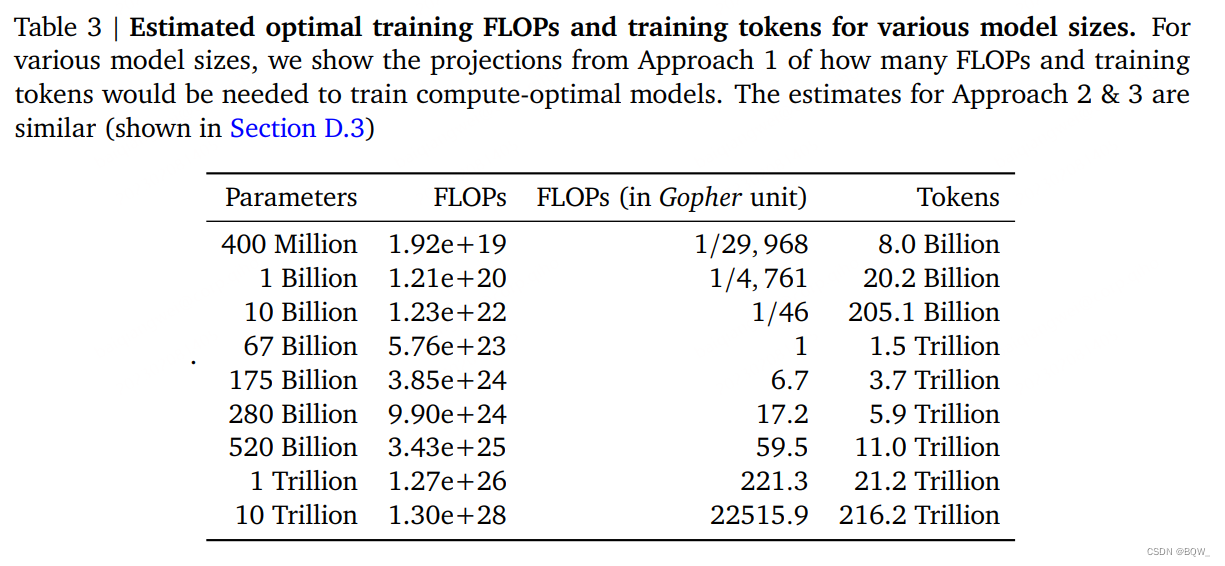
​ 尽管在三种方法中使用了不同的拟合方法和不同的训练模型，其对于给定FLOPs的最优参数规模和token数量产生了类似的预测。所有三种方法都表明，随着计算预算的增加，模型尺寸和训练数据的数量应该等比例的增加。第一和第二种方法返回了非常相似的最优模型尺寸。第三种方法在更大的预算下甚至预测更小的模型是最优。我们注意到，对于低训练FLOPs\text{FLOPs}FLOPs的观测点(L,N,D)(L,N,D)(L,N,D)要比更高的计算预测有更大的残差∥L−L^(N,D)∥22\parallel L-\hat{L}(N,D) \parallel_2^2∥L−L^(N,D)∥22​。

​ 上表3展示了在给定模型尺寸下，达到计算最优边界的FLOPs和tokens数量估计值。我们的发现表明，考虑到各自的计算预算，当前的大语言模型被认为太大了。例如，我们发现175B参数的模型训练应该使用的计算预算为4.41×10244.41\times 10^{24}4.41×1024 FLOPs，并且在4.2万亿的tokens上进行训练。类似于Gopher的280B模型的最优模型的计算代价应该接近102510^{25}1025 FLOPs，并应该在6.8万亿的tokens上进行训练。除非有102610^{26}1026 FLOPs的计算预算，1万亿参数的模型不太可能是训练的最优模型。此外，需要的训练数据远远超过了当前用于训练大模型的数量，除了工程改善来训练更大模型外，也强调了数据收集的重要性。虽然外推几个数量级有很大的不确定性，但我们的分析已经清晰的表明：在给定的训练计算预算下，当前许多的LLM应该使用更小的模型在更多的tokens训练才能实现最优的模型。

三、Chinchilla

​ 基于上面的分析，在Gopher计算代价下的最优模型尺寸介于40B至70B。由于数据集和计算效率的考虑，我们会在1.4T个token上训练70B参数的模型来测试这一假设。我们称这个模型为Chinchilla，并比较其与Gopher和其他LLMs。Chinchilla和Gopher在相同数量的FLOPs上训练，但是模型尺寸和训练的token数量不同。

​ 虽然预训练大语言模型具有相当大的计算代价，下游的微调和推理也会占用大量的计算量。由于比Gopher小4倍，Chinchilla的显存占用和推理代价也会更小。

1. 模型和训练细节

​ 训练Chinchilla的所有超参数在上表4中展示。除了下面列出的以外，Chinchilla使用与Gopher相同的模型架构和训练设置。

• 我们在MassiveText上训练Chinchilla(与Gopher相同的数据集)，但是使用稍微不同的子集分布，从而增加训练tokens的数量。
• Chinchilla使用AdamW而不是Adam，其能够改善语言建模的loss以及经过微调后的下游任务表现。
• 我们使用简单修改的SentencePiece tokenizer来训练Chinchilla，其不应用NFKC规范化。词表非常的类似，94.15%的tokens与训练Gopher相同。我们发现这有助于表示数学和化学。
• 在正向和后向传播中使用bfloat16，我们在分布式优化器状态中的权重保存为float32。

2. 结果

​ 我们对Chinchilla进行了广泛的评估，与各种LLM进行了比较。我们评估的任务如上表5所示。因为本文专注在最优的模型尺寸上，我们包含了大量有代表性的子集，并引入了新的评估来更好的与现有的大模型进行比较。

2.1 语言建模

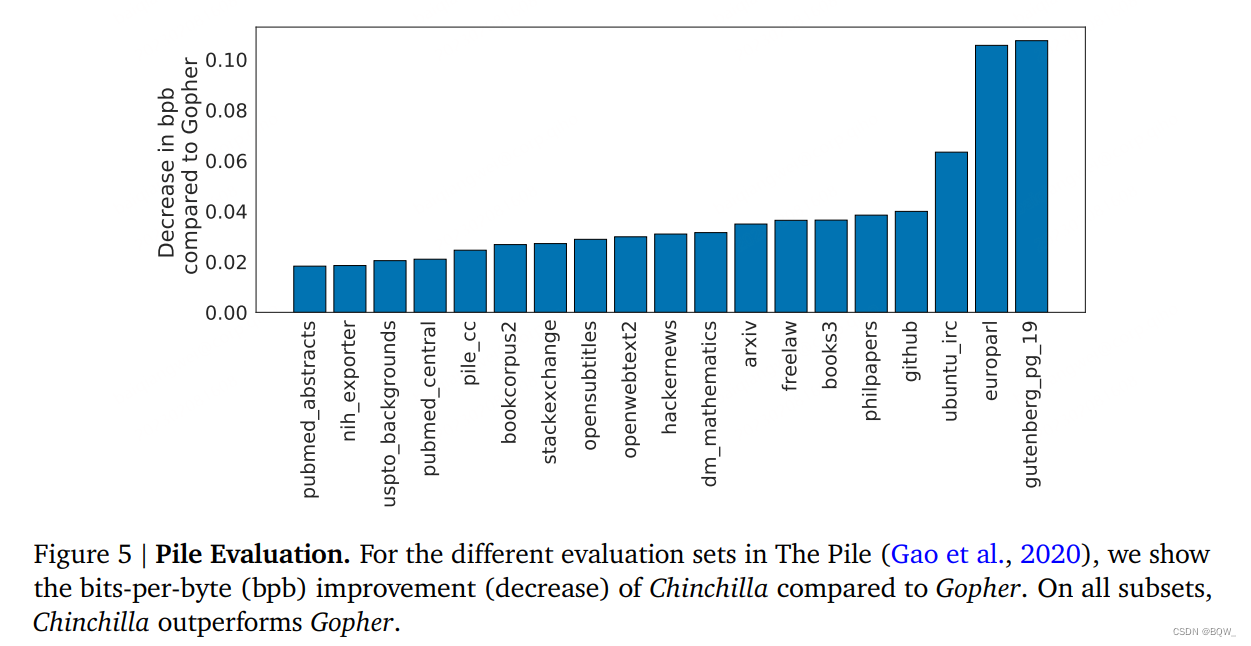
​ 如上图5所示，Chinchilla在Pile的所有评估子集上都显著超越了Gopher。相比于Jurssic-1(178B)，Chinchilla在除了子集dm_mathematics和ubuntu_irc上的所有任务上表现更优。在Wikitext103上，Chinchilla实现了困惑度为7.16，而Gopher为7.75。在这些语言建模基准上比较Chinchilla和Gopher需要谨慎，因为其训练数据是Gopher的4倍，因此存在训练/测试集泄露导致的结果提高。因此，我们更加关注其他不太关心泄露的任务，例如：MMLU、BIG-bench以及各种闭卷问答和常识分析。

2.2 MMLU

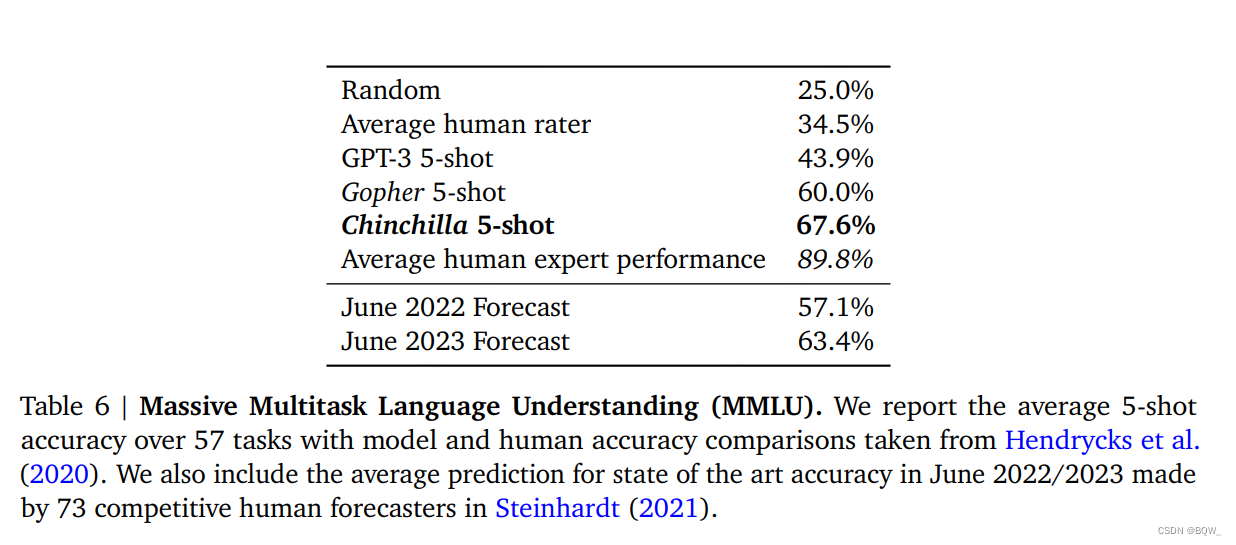
​ MMLU(Massive Multitask Language Understanding)基准是由一系列学术科目中类似考试的问题组成。在上表6中，我们报告了Chinchilla在MMLU上5-shot的平均效果。在这个基准上，尽管更小但是Chinchilla显著优于Gopher，平均准确率67.6%。Chinchilla甚至超越了2023年6月专家预测的63.4%准确率。此外，Chinchilla在4个独立的任务上实现了超越90%的准确率：high_school_gov_and_politics、international_law、sociology和us_foreign_policy。据我们所知，没有模型能够在该子集中实现超过90%的准确率。

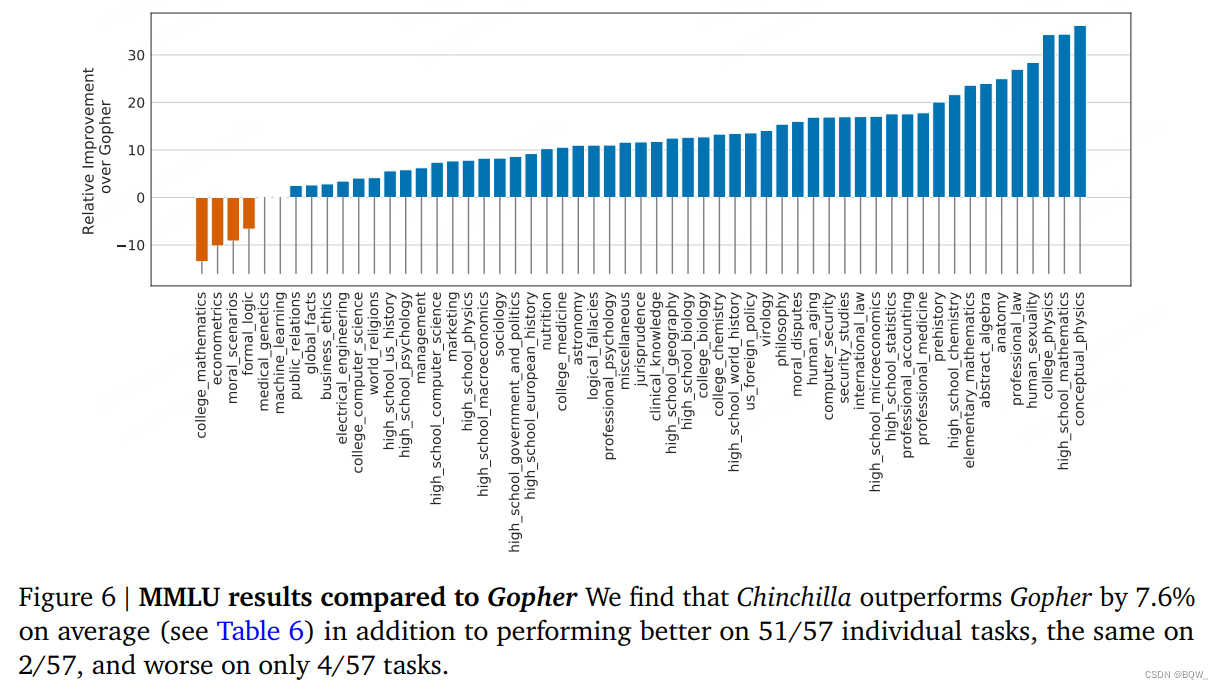
​ 在上图6中，我们展示了在分解子任务上与Gopher的比较。总的来说，我们发现Chinchilla在绝大多数任务上改善了效果。在4个任务上Chinchilla差于Gopher，在2个任务上没有改变。

2.3 阅读理解

​ 在最后单词预测数据集LAMBADA上，Chinchilla实现了77.4%的准确率，相比于Gopher的74.5%和MT-NLG 530B的76.6%。在RACE-h和RACE-m上，Chinchilla显著优于Gopher，在两个case上改善超过10%。

2.4 BIG-bench

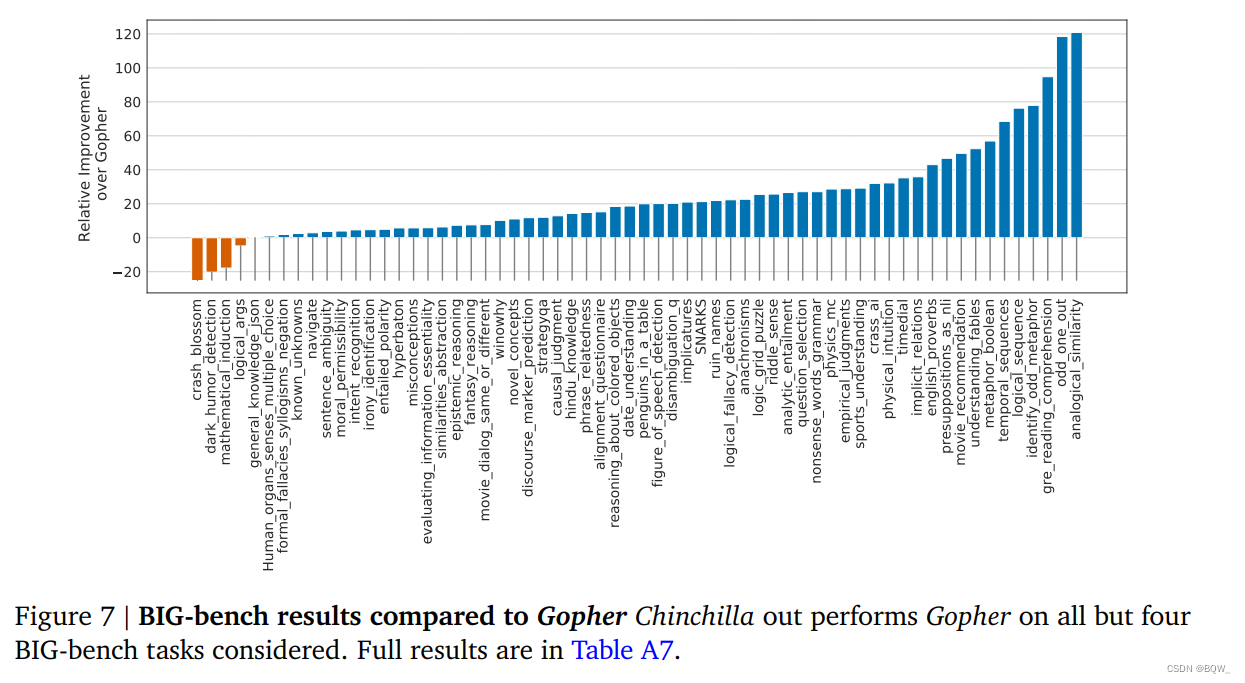
​ 我们在BIG-bench任务上分析了Chinchilla。类似于我们在MMLU中观察到的，Chinchilla在绝大多数任务上优于Gopher(如上图7所示)。我们发现Chinchilla平均改善10.7%，准确率达到了65.1%，相比于54.4%的Gopher。在我们考虑的62个任务中，Chinchilla效果差于Gopher的仅有4个：crash_blossom、dark_humor_detection、mathematical_induction和logical_args。

2.5 常识

​ 我们在各种常识基准上评估Chinchilla：PIQA、SIQA、Winogrande、HellaSwag和BoolQ。我们发现Chinchilla在所有任务上都优于Gopher和GPT-3，并且在除了一个任务以外的所有任务都优于MT-NLG 530B。

​ 在TruthfulQA上，Chinchilla在0-shot、5-shot和10-shot上达到了43.6%、58.5%和66.7%。相比之下，Gopher在0-shot上实现了29.5%，10-shot上实现了43.7%。与Lin et al.等人的发现相比，Chinchilla实现了更好的效果，仅仅是更好的建模预训练数据就可以带来该基准的大幅度改善。

2.6 闭卷问答

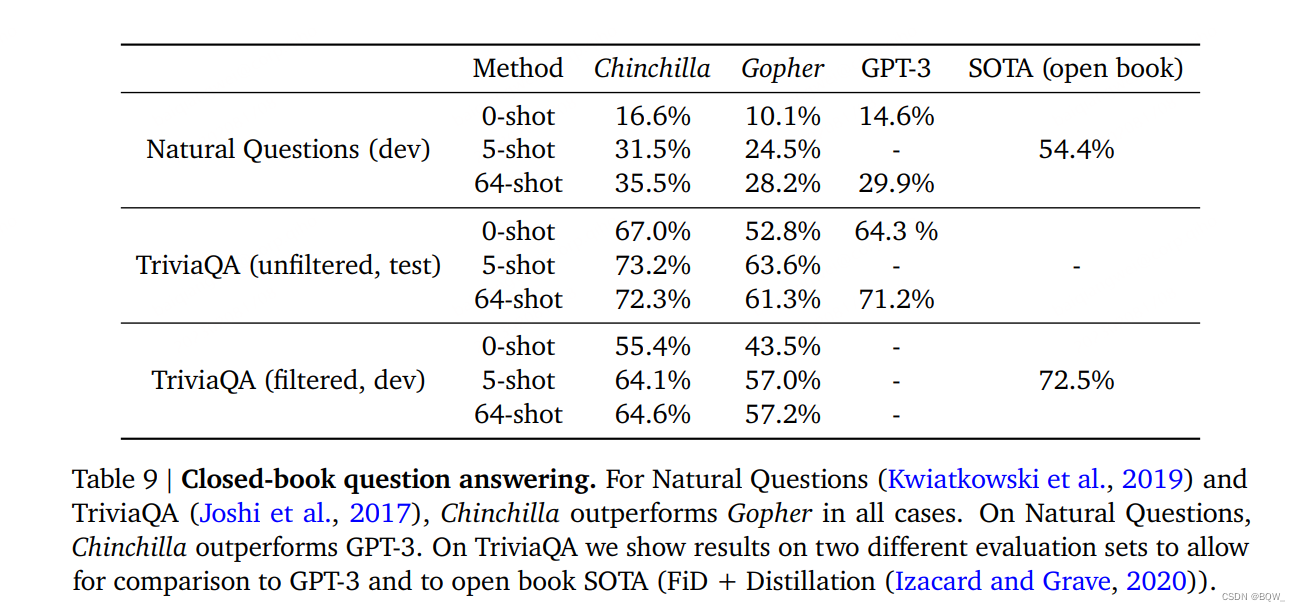
闭卷问答基准的结果如上表9所示。在Natural Question数据集中，Chinchilla实现了新的闭卷SOTA准确率：5-shot的31.5%和64-shot的35.5%，相比于Gopher的21%和28%。在TriviaQA上，我们展示了过滤集和未过滤集。在两种cases中，Chinchilla显著的优于Gopher。在过滤版本中，Chinchilla仅落后于SOTA 7.9%个点。在未过滤集中，Chinchilla超越了GPT-3。

本文链接：https://my.lmcjl.com/post/7856.html