Pytorch中使用backward()求导详解_comli_cn的博客-CSDN博客_backward pytorch
主要参考此篇文献,在个人理解的基础上做一些补充,希望能够帮助大家理解,如果有错误欢迎大家指出,谢谢。
1.out.backwark()中out是一个标量
import torch
from torch.autograd import Variable#生成一个内容为[2,3]的张量,Varibale 默认是不要求梯度的,如果要求梯度,
#需要加上requires_grad=True来说明
#这里的Variable是为了设置变量,把a0=2,a1=3设置为两个变量
a = Variable(torch.tensor([2,3]),requires_grad=True)
b = a+3
c = b*3
out=c.mean() #求均值
out.backward()
print("a=",a)
print("out=",out)
print(a.grad) #求out对a的偏导
结果为
a= tensor([2., 3.], requires_grad=True)
out= tensor(16.5000, grad_fn=<MeanBackward0>)
tensor([1.5000, 1.5000])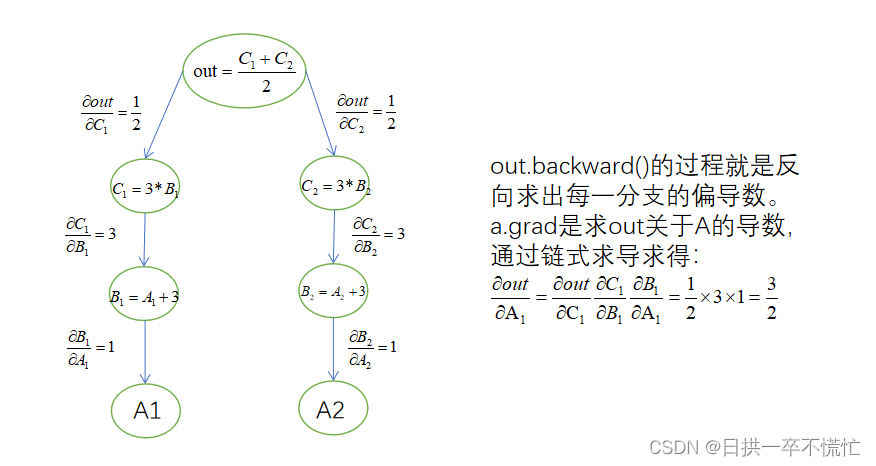
2. out.backward()中的out是一个向量(或者理解成1xN的矩阵)
import torch
from torch.autograd import Variable#生成一个内容为[2,4]的张量,Varibale 默认是不要求梯度的,如果要求梯度,
#需要加上requires_grad=True来说明
a = Variable(torch.Tensor([[2,4]]),requires_grad=True)
b = torch.zeros(1,2)
b[0,0] = a[0,0]**2+a[0,1]
b[0,1] = a[0,1]**3+a[0,0]
out = 2*b#括号里面的参数要传入和out维度一样的矩阵
#这个矩阵里面的元素会作为最后加权输出的权重系数
out.backward(torch.FloatTensor([[1,2]]))
print("a=",a)
print("out=",out)
print(a.grad) #求out对a的偏导
结果为
a= tensor([[2., 4.]], requires_grad=True)
out= tensor([[ 16., 132.]], grad_fn=<MulBackward0>)
tensor([[12., 194.]])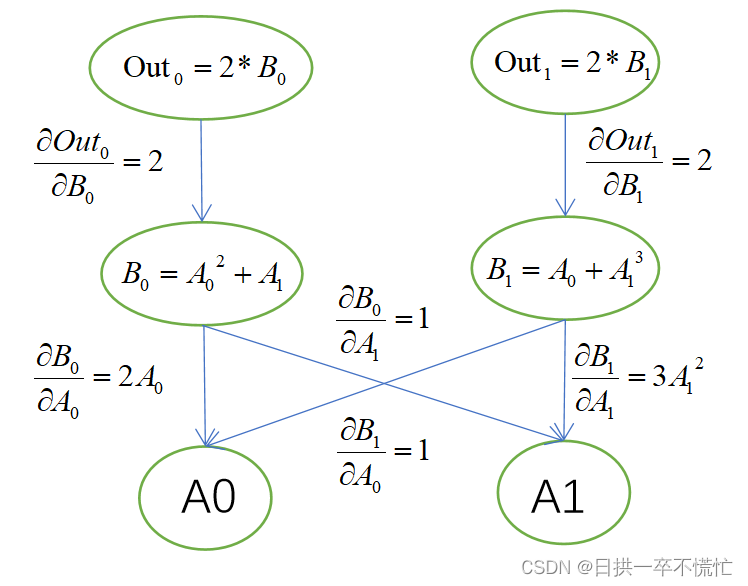

输出对输入的偏导遵循雅克比行列式的形式(个人理解:输出个数决定行,输入个数决定列)
out.backward(torch.FloatTensor([[1,2]]))
由于 out.backward括号里的参数需要与out的形状相同,所以参数的含义是所有输出对所有输入求导加权系数,表达如下:
Pytorch中的自动求导函数backward()所需参数含义 - 不愿透漏姓名的王建森 - 博客园 (cnblogs.com)

参数在与导数结果加权时,将传入的参数看做行向量与结果矩阵相乘,所以结果输出为[12,194]

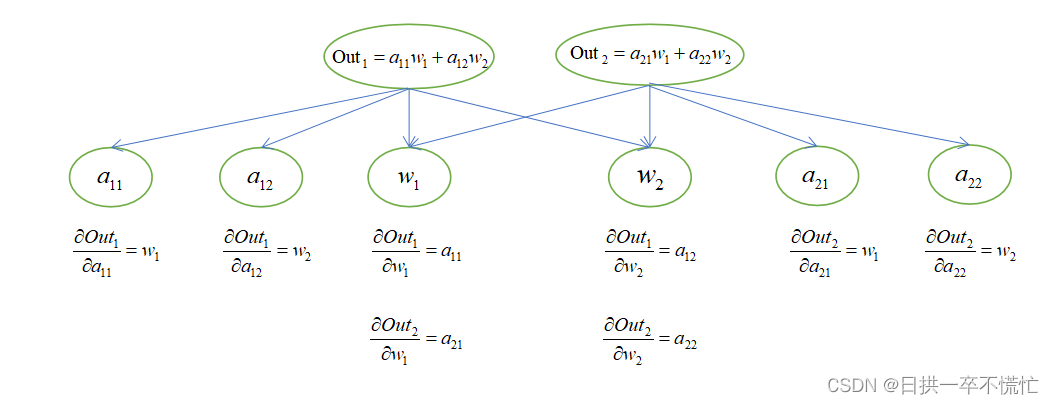
3. out.backward()中的out是一个矩阵
矩阵和向量的求导法则_Icoding_F2014的博客-CSDN博客_矩阵对向量求导
import torch
from torch.autograd import Variable#生成一个内容为[2,3]的张量,Varibale 默认是不要求梯度的,如果要求梯度,
#需要加上requires_grad=True来说明
a = Variable(torch.Tensor([[2,3],[1,2]]),requires_grad=True)
w = Variable(torch.Tensor([[2],[1]]),requires_grad=True)
out = torch.mm(a,w)#括号里面的参数要传入和out维度一样的矩阵
#这个矩阵里面的元素会作为最后加权输出的权重系数
out.backward(torch.FloatTensor([[1],[1]]))
print("a gradients are:{}".format(a.grad.data))
print("w gradients are:{}".format(w.grad.data))结果为
a gradients are:tensor([[2., 1.],[2., 1.]])
w gradients are:tensor([[3.],[5.]])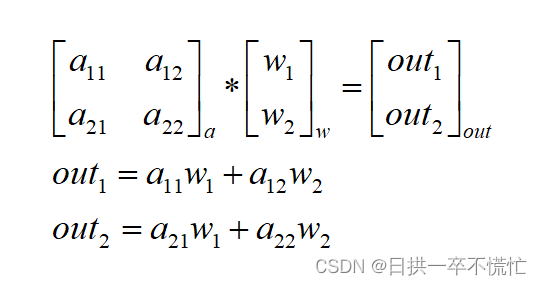
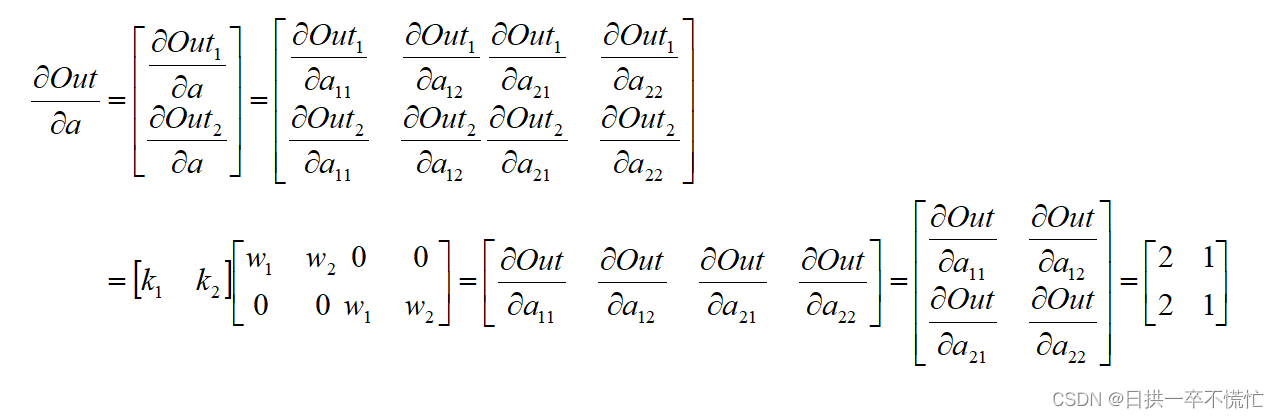
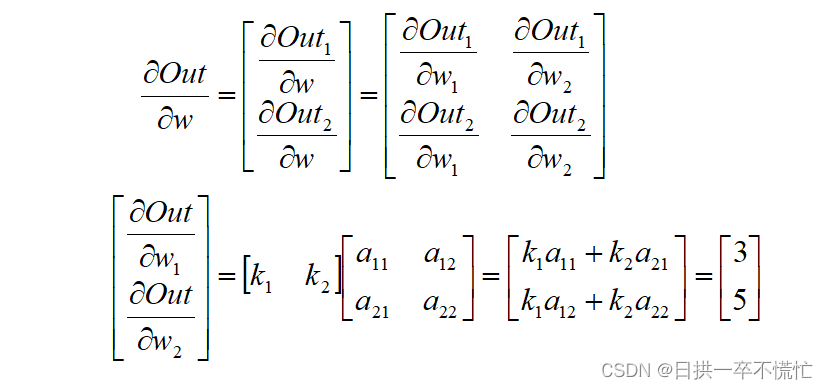
最后,感谢在解决问题过程中各位大佬的帮助,如果我的回答帮助到你,还麻烦给我点赞加油呀~~
本文链接:https://my.lmcjl.com/post/11340.html
展开阅读全文

4 评论