自然语言处理的重要范式包括对通用域数据的大规模预训练以及对特定任务或领域的适应。随着我们预先培训较大的模型,重新训练所有模型参数的完整微调变得越来越不可行。以GPT-3 175B为例 - 部署微型模型的独立实例,每个实例具有175B参数,非常昂贵。我们提出了低排名的适应性或LORA,它冻结了预先训练的模型权重,并注入了可训练的等级分解矩阵中的各层变压器体系结构,从而大大减少了下游任务的可训练参数的数量。与ADAM微调的GPT-3 175B相比,LORA可以将可训练参数的数量减少10,000次,而GPU内存的需求量降低了3次。洛拉(Lora)在罗伯塔(Roberta),迪伯塔(Deberta),GPT-2和GPT-3上的模型质量进行了比较或更好,尽管具有较少的训练参数,更高的训练吞吐量,并且与适配器不同,没有额外的推断潜伏期。我们还提供了对语言模型适应中排名缺陷的实证研究,该研究阐明了洛拉的功效。我们发布了一个软件包,可在此HTTPS URL上为Roberta,Deberta和GPT-2提供洛拉与Pytorch模型的集成,并为我们的实现和模型检查点。
1. LORA原理介绍
LORA的论文写的比较难读懂,但是其原理其实并不复杂。简单理解一下,就是在模型的Linear层,的旁边,增加一个“旁支”,这个“旁支”的作用,就是代替原有的参数矩阵W进行训练。
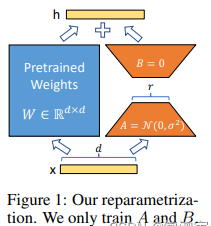
结合上图,我们来直观地理解一下这个过程,输入x ,具有维度d ,举个例子,在普通的transformer模型中,这个x 可能是embedding的输出,也有可能是上一层transformer layer的输出,而d一般就是768或者1024。按照原本的路线,它应该只走左边的部分,也就是原有的模型部分。
而在LORA的策略下,增加了右侧的“旁支”,也就是先用一个Linear层A,将数据从d dd维降到r rr,这个r rr也就是LORA的秩,是LORA中最重要的一个超参数。一般会远远小于d dd,尤其是对于现在的大模型,d dd已经不止是768或者1024,例如LLaMA-7B,每一层transformer有32个head,这样一来d 就达到了4096.
接着再用第二个Linear层B,将数据从r变回d维。最后再将左右两部分的结果相加融合,就得到了输出的hidden_state。
对于左右两个部分,右侧看起来像是左侧原有矩阵W的分解,将参数量从d ∗ d 变成了d*r+d*r,在r < < d 的情况下,参数量就大大地降低了。熟悉各类预训练模型的同学可能会发现,这个思想其实与Albert的思想有异曲同工之处,在Albert中,作者通过两个策略降低了训练的参数量,其一是Embedding矩阵分解,其二是跨层参数共享。
在Albert中,作者考虑到词表的维度很大,所以将Embedding矩阵分解成两个相对较小的矩阵,用来模拟Embedding矩阵的效果,这样一来需要训练的参数量就减少了很多。
LORA也是类似的思想,并且它不再局限于Embedding层,而是所有出现大矩阵的地方,理论上都可以用到这样的分解。
但是与Albert不同的是,Albert直接用两个小矩阵替换了原来的大矩阵,而LORA保留了原来的矩阵W,但是不让W参与训练,所以需要计算梯度的部分就只剩下旁支的A和B两个小矩阵。
从论文中的公式来看,在加入LORA之前,模型训练的优化表示为:
其中,模型的参数用Φ 表示。
而加入了LORA之后,模型的优化表示为:
其中,模型原有的参数是Φ 0 \Phi_0Φ
0
,LORA新增的参数是Δ Φ ( Θ ) \Delta \Phi\left(\Theta\right)ΔΦ(Θ)。
从第二个式子可以看到,尽管参数看起来增加了(多了Δ Φ ( Θ ) \Delta \Phi\left(\Theta\right)ΔΦ(Θ)),但是从前面的max的目标来看,需要优化的参数只有Θ \ThetaΘ,而根据假设,Θ < < Φ \Theta <<\PhiΘ<<Φ,这就使得训练过程中,梯度计算量少了很多,所以就在低资源的情况下,我们可以只消耗Θ \ThetaΘ这部分的资源,这样一来就可以在单卡低显存的情况下训练大模型了。
但是相应地,引入LORA部分的参数,并不会在推理阶段加速,因为在前向计算的时候,Φ \PhiΦ部分还是需要参与计算的,而Θ \ThetaΘ部分是凭空增加了的参数,所以理论上,推理阶段应该比原来的计算量增大一点。
本文链接:https://my.lmcjl.com/post/13598.html

4 评论