一、目的

使用Matlab分析与设计实验，理解与掌握以下知识点：
1、信号的采样、频谱混叠
2、信号的频谱分析
3、信号的幅度调制与解调方法
4、理想滤波器的时域和频域特性
5、数字滤波器的设计与实现

二、内容

1、录制一段个人的语音信号
2、采用合适的频率，对录制的信号进行采样，画出采样前后语音信号的时域波形和频谱图
3、给原始语音信号加噪声，画出加噪声后的语音信号的时域波形和频谱图
4、在频域内进行分析和设计一个理想带通传输信道
5、对3所述的语音信号进行幅度调制，画出调制后的语音信号的时域波形和频谱图
6、利用4给出的理想带通信道对信号进行传输
7、在接收端对接收到的信号进行解调，画出解调后的语音信号的时域波形和频谱图
8、设计性能良好的滤波器对7得到的信号进行滤波，画出滤波后的语音信号的时域波形和频谱图
9、对原始（加噪声前）语音信号进行回放，并与8所得到滤波后的语音信号进行对比（时域波形、频谱图、听觉等）

三、系统架构设计

四、设计原理及步骤

1. 降采样

语音信号是一种模拟信号，但它在存储到计算机中时会被转化为数字信号，此时的采样频率比较高。在实际使用时，我们并不需要这么高的采样频率。因此，需要对语音信号进行降采样。
在确定降采样频率时，必须要考虑到两点。其一，根据奈奎斯特理论，采样频率必须高于声音信号最高频率的两倍，这样才能把数字信号表示的声音还原成为原来的声音。在实际应用中，一般取信号频率上限的3_{5倍作为采样频率。在正常情况下，人声带发出的声音在300}3400 Hz[1]，因此对于单纯的语音信号来说，采样频率大于10.2kHz即可。其二，考虑到后面有调制与解调的过程，且载波频率必须小于采样频率的一半，因此适当将采样频率提高为21kHz。
降采样前后的语音信号的时域波形和频谱图如下：

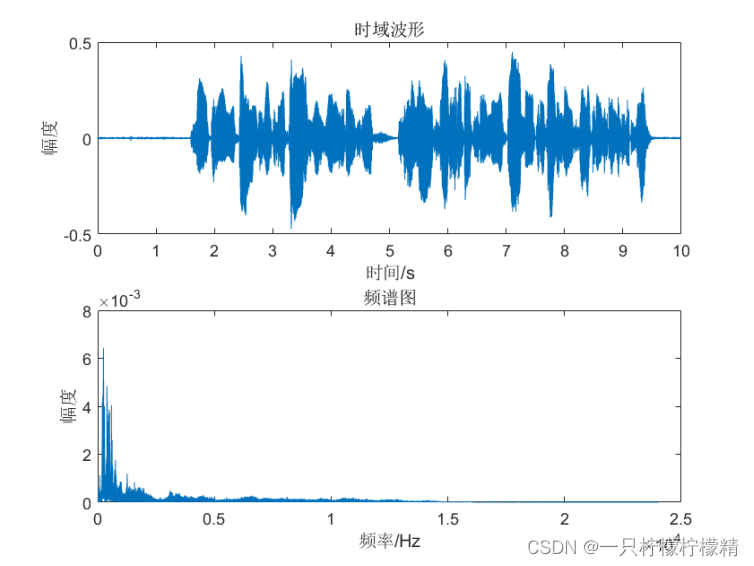
2. 高斯白噪声

高斯白噪声是分析信道加性噪声的理想模型，它的瞬时值服从高斯分布，而它的功率谱密度服从均匀分布。在Matlab中，wgn函数可以用于产生高斯白噪声，而awgn函数可以用于在某一信号中加入指定信噪比的高斯白噪声。信噪比是指一个电子设备或者电子系统中信号与噪声的比例。一般来说，信噪比越大，混在信号里的噪声越小，声音回放的音质越高，否则相反。
此外，在Matlab中也可以使用randn函数来产生高斯白噪声。这种方法利用了高斯白噪声的幅度分布服从高斯分布的特点，可以方便地指定它的均值和方差。
加入高斯白噪声后的语音信号的时域波形和频谱图如下：

3. 调制

使用振幅调制（AM）的方法对加噪声后的语音信号进行调制：将语音信号与一直流信号相加，再与载波信号相乘。与双边带调制（DSB）相比，振幅调制可在接收端省去本地载波，降低接收机的成本。
振幅调制后的语音信号的时域波形和频谱图如下：

图5中的两个频谱图在本质上是一样的。其中，频谱图2是对频谱图1的纵坐标范围加以限制得到的。从图中我们可以发现，由于载波信号是一个cos函数，它的傅里叶变换是冲激函数的形式，有非常大的能量，在频谱图中的幅度远远大于其他频率的信号。因此，振幅调制虽然可以降低接收机的成本，但付出的代价是要使用价格昂贵的发射机，提供足够强的信号Acos(w0t)的附加功率。但这也是合算的，因为往往对于大批的接收机来说，只有一个发射机。

4、理想带通传输信道的设计

也即设计一个理想带通滤波器。带通滤波器是指能通过某一频率范围内的频率分量，但将其他的频率分量衰减到极低水平的滤波器。一个理想的带通滤波器应该有一个完全平坦的通带，在通带内没有放大或者衰减，并且在通带之外所有频率都被完全衰减掉。因此，理想的带通滤波器不能使用Matlab中的Filter Designer工具箱直接进行设计。可以使用窗函数（矩形窗boxcar）法设计FIR滤波器，也可以在频域中直接对语音信号的频谱进行操作。
语音信号通过理想带通传输信道进行传输后，其时域波形和频谱图如下：

5. 解调

对振幅调制（AM）的信号进行解调有很多种方法。如果载波信号是确定的，则通常可以采用同步检波的方式。这种方式的信噪比最好，对信号中混入的噪声的抑制能力也最强[3]。上文中提到的双边带调制（DSB）的信号也可以使用这种方法进行解调。但是，当载波信号未知时，同步检波的方法就不再适用了。此时，利用调幅信号的包络反映调制信号波形变化的这一特点，可以使用包络检波的方法进行解调。在本次作业中，为更加贴近实际情况，选择使用包络检波的方法。
包络检波是基于滤波检波的振动信号处理方法，尤其对初期故障和信噪比较低的故障信号识别能力强[2]。将一段时间长度的高频信号的峰值点连线，就可以得到分别位于上方和下方的两条线，这两条线就叫做包络线。而上方的包络线减去调制时加入的直流分量，就可以方便地得到原始信号。
此外，必须注意到的是，由于包络检波器的非线性解调作用，导致包络检波存在着门限效应。在信噪比较小的情况下，调制信号无法与噪声分开，有用信号被淹没在噪声之中，检波器的输出信噪比急剧下降，解调效果很差。由于2中在加入高斯白噪声时选择的信噪比较大，因此可以使用包络检波的方法来进行解调。

图7中的两个频谱图在本质上是一样的。其中，频谱图2是对频谱图1的纵坐标范围加以限制得到的。观察结果可以发现，解调后的频谱图中出现了一些原本并不存在的高频分量（还有少部分意外的频率分量是低频的）。这可能是由包络检波中的“插值”步骤引起的，因为插值过程存在着一定的随机性，插值结果可能不够“光滑”。上图在计算时使用的是三次样条插值方法（spline），这是Matlab支持的所有插值方法中最光滑的插值方法。下面对不同插值方法得到的频谱图进行简单对比。



显然，在Matlab的这四种插值方法中，对于本课题来讲，三次样条插值方法（spline）的效果最好。

6. 滤波去噪

根据5中的分析可知，解调过程导致频谱图中产生了一些原本并不存在的高频信号，因此首先应该设计低通滤波器来滤除这些高频信号。对于低通滤波器来说，低频信号能够正常通过，而超过截止频率的高频信号则被阻隔、减弱。观察原始语音信号的频谱图可以发现，该语音信号的能量大多集中在2kHz以内，因此低通滤波器的截止频率可以设置为2kHz。该低通滤波器可以使用Matlab中的Filter Designer工具箱直接进行设计。设计时，Filter Order可选择Minimum Order（最小阶数）。
此外，要滤除高斯白噪声则比较困难。因为高斯白噪声的频谱是遍布在整个语音信号的频谱中的，通常的低通、高通、带通或者带阻滤波器都无法很好地将它滤除。通过搜集资料得知，高斯白噪声可以通过均值滤波、自适应滤波、卡尔曼滤波和维纳滤波等方式滤除。在本课题中选择维纳滤波器来滤除高斯白噪声。
维纳滤波器是一种以最小平方为最优准则的线性滤波器。在一定的约束条件下，其输出可以与一给定函数的差的平方达到最小，通过数学运算最终变为一个托布利兹方程的求解问题[4]。维纳滤波器与神经网络有一定的相似性，它们在使用时都分为两个阶段，一个是训练阶段，另一个是工作阶段。训练阶段的目的是求出维纳滤波器在特定环境下的系数。当得到满意的系数后，即可进入工作阶段，且在工作阶段该系数不会再改变。在工作阶段，则可以对真正待处理的信号进行去噪处理。
经过实验发现，仅使用维纳滤波器对语音信号滤波一次的效果并不令人满意，仍有较多的噪声残留。因此，为保证有效地滤除噪声，对语音信号进行两次维纳滤波。
经过低通滤波和两次维纳滤波后的语音信号的时域波形和频谱图如下：

7. 语音信号回放

对原始的语音信号和滤波后的语音信号分别进行回放。从听觉的角度来说，滤波后的语音信号中仍然混有部分噪声，且语音信号本身也被削弱了。这可能是因为在使用维纳滤波去除高斯白噪声时，由于它遍布整个频域，导致语音信号也受到了一定的影响。从时域波形来看，可以比较明显地发现噪声并没有被完全地滤除，且原本的语音信号波形也发生了轻微的变化。而从频谱图来看，则可以比较明显地发现6中的低通滤波成功地滤掉了所有高于2kHz的信号，低于2kHz的信号则被比较完整地保留下来了。

总结

从总体上来看，虽然已经较好地完成了作业要求，但仍然有改进的空间。首先，在解调部分使用了包络检波的方法，出现了一些原本并不存在的高频分量。虽然在后期已经使用了低通滤波器进行滤除，但仍然对原始语音信号造成了一定的影响。如果时间允许，应该对其他的解调方式进行探索、尝试和研究，并进一步分析高频分量出现的原因。其次，经过对调制、传输、解调和去噪等过程的模拟后，语音信号本身也被削弱了，可以考虑加入语音信号增强的环节以保证语音信号的质量。

本文链接：https://my.lmcjl.com/post/14255.html